How to design a dataset compliant with an ML-based system ODD?

This paper focuses on a Vision-based Landing task and presents the design and the validation of a dataset that would comply with the Operational Design Domain (ODD) of a Machine-Learning (ML) system. Relying on emerging certification standards, we describe the process for establishing ODDs at both the system and image levels. In the process, we present the translation of high-level system constraints into actionable image-level properties, allowing for the definition of verifiable Data Quality Requirements (DQRs). To illustrate this approach, we use the Landing Approach Runway Detection (LARD) dataset which combines synthetic imagery and real footage, and we focus on the steps required to verify the DQRs. The replicable framework presented in this paper addresses the challenges of designing a dataset compliant with the stringent needs of ML-based systems certification in safety-critical applications.

Quantized Approximately Orthogonal Recurrent Neural Networks

Orthogonal recurrent neural networks (ORNNs) are an appealing option for learning tasks involving time series with long-term dependencies, thanks to their simplicity and computational stability. However, these networks often require a substantial number of parameters to perform well, which can be prohibitive in power-constrained environments, such as compact devices. One approach to address this issue is neural network quantization. The construction of such networks remains an open problem, acknowledged for its inherent instability.In this paper, we explore the quantization of the recurrent and input weight matrices in ORNNs, leading to Quantized approximately Orthogonal RNNs (QORNNs). We investigate one post-training quantization (PTQ) strategy and three quantization-aware training (QAT) algorithms that incorporate orthogonal constraints and quantized weights. Empirical results demonstrate the advantages of employing QAT over PTQ. The most efficient model achieves results similar to state-of-the-art full-precision ORNN and LSTM on a variety of standard benchmarks, even with 3-bits quantization.

DP-SGD Without Clipping: The Lipschitz Neural Network Way

State-of-the-art approaches for training Differentially Private (DP) Deep Neural Networks (DNN) faces difficulties to estimate tight bounds on the sensitivity of the network's layers, and instead rely on a process of per-sample gradient clipping. This clipping process not only biases the direction of gradients but also proves costly both in memory consumption and in computation. To provide sensitivity bounds and bypass the drawbacks of the clipping process, our theoretical analysis of Lipschitz constrained networks reveals an unexplored link between the Lipschitz constant with respect to their input and the one with respect to their parameters. By bounding the Lipschitz constant of each layer with respect to its parameters we guarantee DP training of these networks. This analysis not only allows the computation of the aforementioned sensitivities at scale but also provides leads on to how maximize the gradient-to-noise ratio for fixed privacy guarantees. To facilitate the application of Lipschitz networks and foster robust and certifiable learning under privacy guarantees, we provide a Python package that implements building blocks allowing the construction and private training of such networks.

When adversarial attacks become interpretable counterfactual explanations

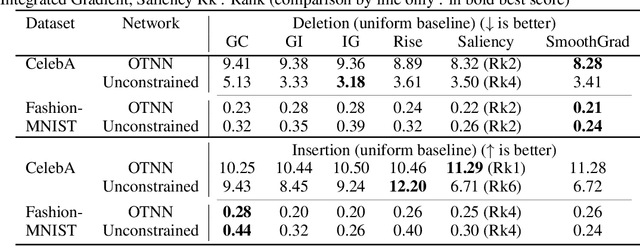
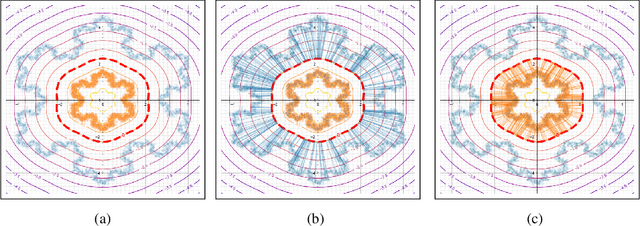
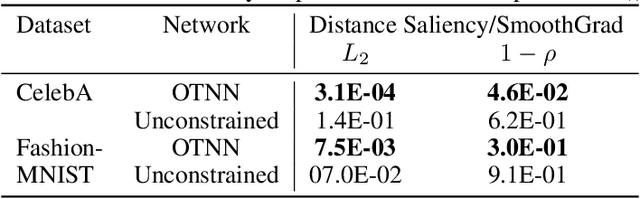
We argue that, when learning a 1-Lipschitz neural network with the dual loss of an optimal transportation problem, the gradient of the model is both the direction of the transportation plan and the direction to the closest adversarial attack. Traveling along the gradient to the decision boundary is no more an adversarial attack but becomes a counterfactual explanation, explicitly transporting from one class to the other. Through extensive experiments on XAI metrics, we find that the simple saliency map method, applied on such networks, becomes a reliable explanation, and outperforms the state-of-the-art explanation approaches on unconstrained models. The proposed networks were already known to be certifiably robust, and we prove that they are also explainable with a fast and simple method.

The Many Faces of 1-Lipschitz Neural Networks

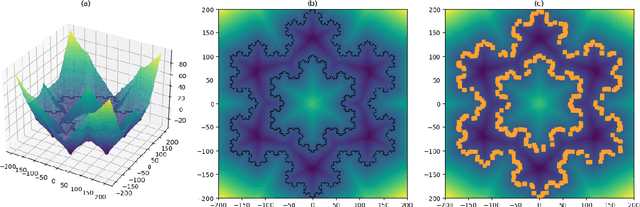
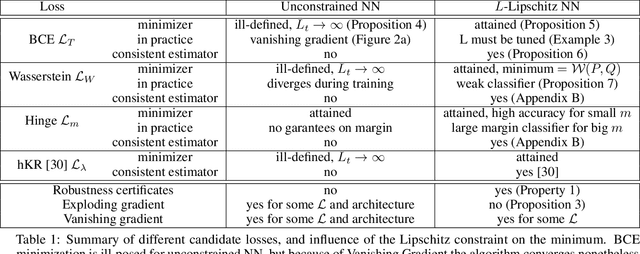
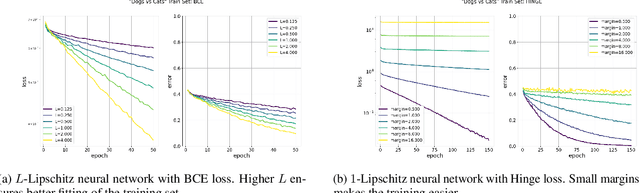
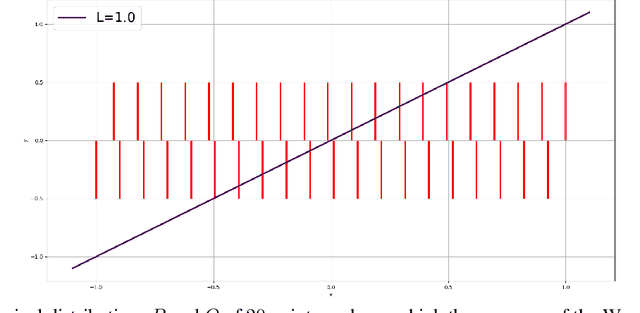
Lipschitz constrained models have been used to solve specifics deep learning problems such as the estimation of Wasserstein distance for GAN, or the training of neural networks robust to adversarial attacks. Regardless the novel and effective algorithms to build such 1-Lipschitz networks, their usage remains marginal, and they are commonly considered as less expressive and less able to fit properly the data than their unconstrained counterpart. The goal of the paper is to demonstrate that, despite being empirically harder to train, 1-Lipschitz neural networks are theoretically better grounded than unconstrained ones when it comes to classification. To achieve that we recall some results about 1-Lipschitz function in the scope of deep learning and we extend and illustrate them to derive general properties for classification. First, we show that 1-Lipschitz neural network can fit arbitrarily difficult frontier making them as expressive as classical ones. When minimizing the log loss, we prove that the optimization problem under Lipschitz constraint is well posed and have a minimum, whereas regular neural networks can diverge even on remarkably simple situations. Then, we study the link between classification with 1-Lipschitz network and optimal transport thanks to regularized versions of Kantorovich-Rubinstein duality theory. Last, we derive preliminary bounds on their VC dimension.

White Paper Machine Learning in Certified Systems

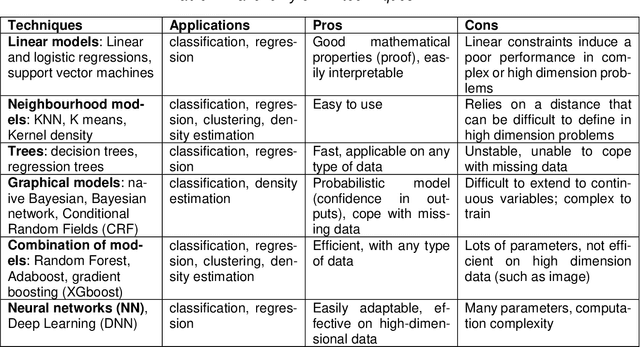
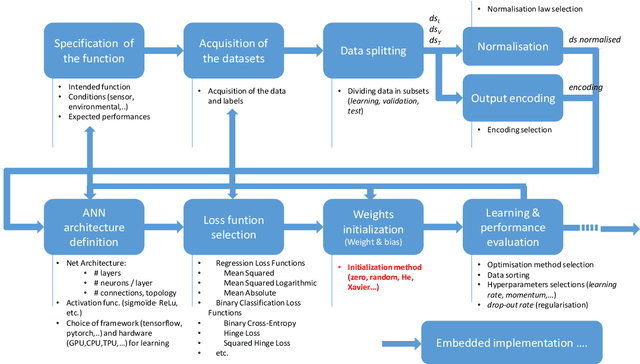
Machine Learning (ML) seems to be one of the most promising solution to automate partially or completely some of the complex tasks currently realized by humans, such as driving vehicles, recognizing voice, etc. It is also an opportunity to implement and embed new capabilities out of the reach of classical implementation techniques. However, ML techniques introduce new potential risks. Therefore, they have only been applied in systems where their benefits are considered worth the increase of risk. In practice, ML techniques raise multiple challenges that could prevent their use in systems submitted to certification constraints. But what are the actual challenges? Can they be overcome by selecting appropriate ML techniques, or by adopting new engineering or certification practices? These are some of the questions addressed by the ML Certification 3 Workgroup (WG) set-up by the Institut de Recherche Technologique Saint Exup\'ery de Toulouse (IRT), as part of the DEEL Project.

Achieving robustness in classification using optimal transport with hinge regularization

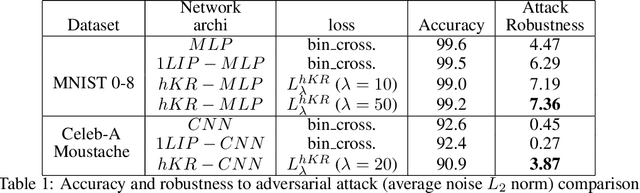
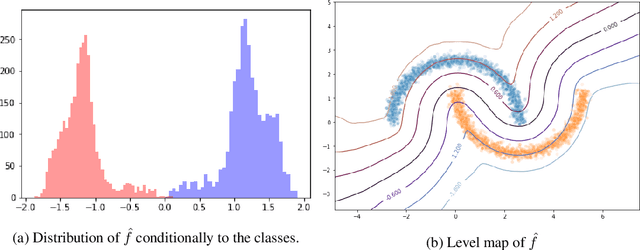
We propose a new framework for robust binary classification, with Deep Neural Networks, based on a hinge regularization of the Kantorovich-Rubinstein dual formulation for the estimation of the Wasserstein distance. The robustness of the approach is guaranteed by the strict Lipschitz constraint on functions required by the optimization problem and direct interpretation of the loss in terms of adversarial robustness. We prove that this classification formulation has a solution, and is still the dual formulation of an optimal transportation problem. We also establish the geometrical properties of this optimal solution. We summarize state-of-the-art methods to enforce Lipschitz constraints on neural networks and we propose new ones for convolutional networks (associated with an open source library for this purpose). The experiments show that the approach provides the expected guarantees in terms of robustness without any significant accuracy drop. The results also suggest that adversarial attacks on the proposed models visibly and meaningfully change the input, and can thus serve as an explanation for the classification.