Improving Out-of-Distribution Detection by Combining Existing Post-hoc Methods

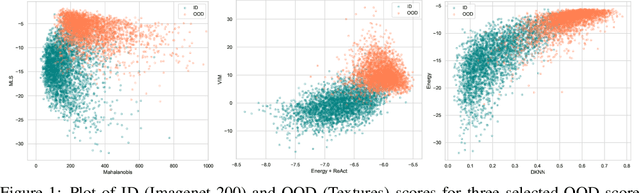
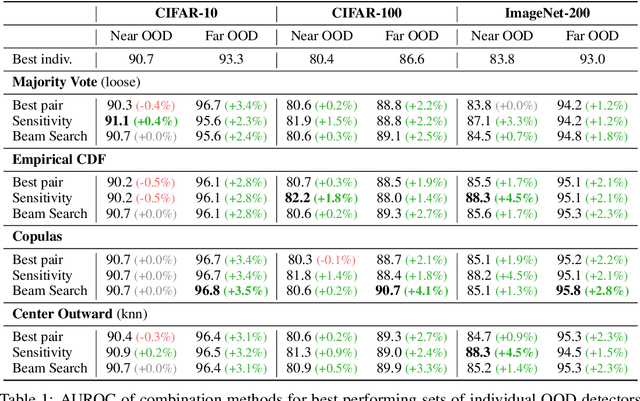
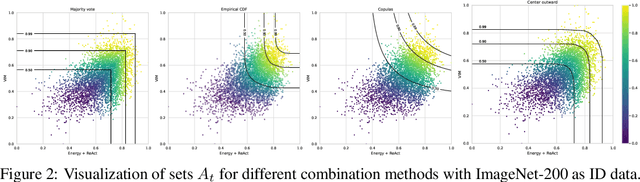
Since the seminal paper of Hendrycks et al. arXiv:1610.02136, Post-hoc deep Out-of-Distribution (OOD) detection has expanded rapidly. As a result, practitioners working on safety-critical applications and seeking to improve the robustness of a neural network now have a plethora of methods to choose from. However, no method outperforms every other on every dataset arXiv:2210.07242, so the current best practice is to test all the methods on the datasets at hand. This paper shifts focus from developing new methods to effectively combining existing ones to enhance OOD detection. We propose and compare four different strategies for integrating multiple detection scores into a unified OOD detector, based on techniques such as majority vote, empirical and copulas-based Cumulative Distribution Function modeling, and multivariate quantiles based on optimal transport. We extend common OOD evaluation metrics -- like AUROC and FPR at fixed TPR rates -- to these multi-dimensional OOD detectors, allowing us to evaluate them and compare them with individual methods on extensive benchmarks. Furthermore, we propose a series of guidelines to choose what OOD detectors to combine in more realistic settings, i.e. in the absence of known OOD data, relying on principles drawn from Outlier Exposure arXiv:1812.04606. The code is available at https://github.com/paulnovello/multi-ood.

DP-SGD Without Clipping: The Lipschitz Neural Network Way

State-of-the-art approaches for training Differentially Private (DP) Deep Neural Networks (DNN) faces difficulties to estimate tight bounds on the sensitivity of the network's layers, and instead rely on a process of per-sample gradient clipping. This clipping process not only biases the direction of gradients but also proves costly both in memory consumption and in computation. To provide sensitivity bounds and bypass the drawbacks of the clipping process, our theoretical analysis of Lipschitz constrained networks reveals an unexplored link between the Lipschitz constant with respect to their input and the one with respect to their parameters. By bounding the Lipschitz constant of each layer with respect to its parameters we guarantee DP training of these networks. This analysis not only allows the computation of the aforementioned sensitivities at scale but also provides leads on to how maximize the gradient-to-noise ratio for fixed privacy guarantees. To facilitate the application of Lipschitz networks and foster robust and certifiable learning under privacy guarantees, we provide a Python package that implements building blocks allowing the construction and private training of such networks.