Deep Sturm--Liouville: From Sample-Based to 1D Regularization with Learnable Orthogonal Basis Functions

Although Artificial Neural Networks (ANNs) have achieved remarkable success across various tasks, they still suffer from limited generalization. We hypothesize that this limitation arises from the traditional sample-based (0--dimensionnal) regularization used in ANNs. To overcome this, we introduce \textit{Deep Sturm--Liouville} (DSL), a novel function approximator that enables continuous 1D regularization along field lines in the input space by integrating the Sturm--Liouville Theorem (SLT) into the deep learning framework. DSL defines field lines traversing the input space, along which a Sturm--Liouville problem is solved to generate orthogonal basis functions, enforcing implicit regularization thanks to the desirable properties of SLT. These basis functions are linearly combined to construct the DSL approximator. Both the vector field and basis functions are parameterized by neural networks and learned jointly. We demonstrate that the DSL formulation naturally arises when solving a Rank-1 Parabolic Eigenvalue Problem. DSL is trained efficiently using stochastic gradient descent via implicit differentiation. DSL achieves competitive performance and demonstrate improved sample efficiency on diverse multivariate datasets including high-dimensional image datasets such as MNIST and CIFAR-10.

Improving Out-of-Distribution Detection by Combining Existing Post-hoc Methods

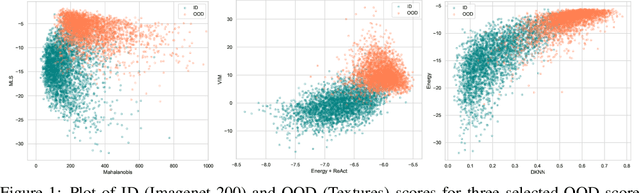
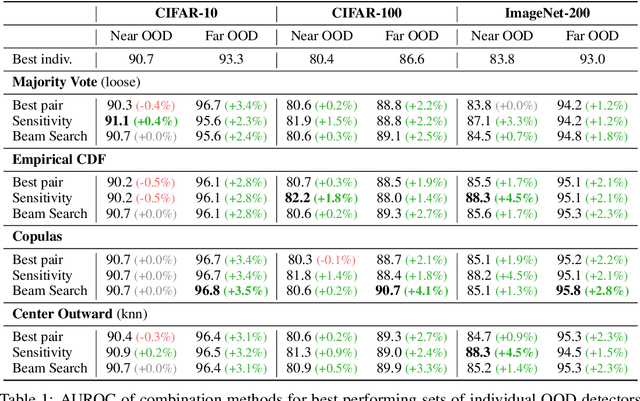
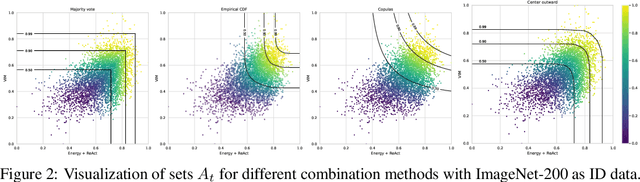
Since the seminal paper of Hendrycks et al. arXiv:1610.02136, Post-hoc deep Out-of-Distribution (OOD) detection has expanded rapidly. As a result, practitioners working on safety-critical applications and seeking to improve the robustness of a neural network now have a plethora of methods to choose from. However, no method outperforms every other on every dataset arXiv:2210.07242, so the current best practice is to test all the methods on the datasets at hand. This paper shifts focus from developing new methods to effectively combining existing ones to enhance OOD detection. We propose and compare four different strategies for integrating multiple detection scores into a unified OOD detector, based on techniques such as majority vote, empirical and copulas-based Cumulative Distribution Function modeling, and multivariate quantiles based on optimal transport. We extend common OOD evaluation metrics -- like AUROC and FPR at fixed TPR rates -- to these multi-dimensional OOD detectors, allowing us to evaluate them and compare them with individual methods on extensive benchmarks. Furthermore, we propose a series of guidelines to choose what OOD detectors to combine in more realistic settings, i.e. in the absence of known OOD data, relying on principles drawn from Outlier Exposure arXiv:1812.04606. The code is available at https://github.com/paulnovello/multi-ood.

Out-of-Distribution Detection Should Use Conformal Prediction (and Vice-versa?)

Research on Out-Of-Distribution (OOD) detection focuses mainly on building scores that efficiently distinguish OOD data from In Distribution (ID) data. On the other hand, Conformal Prediction (CP) uses non-conformity scores to construct prediction sets with probabilistic coverage guarantees. In this work, we propose to use CP to better assess the efficiency of OOD scores. Specifically, we emphasize that in standard OOD benchmark settings, evaluation metrics can be overly optimistic due to the finite sample size of the test dataset. Based on the work of (Bates et al., 2022), we define new conformal AUROC and conformal FRP@TPR95 metrics, which are corrections that provide probabilistic conservativeness guarantees on the variability of these metrics. We show the effect of these corrections on two reference OOD and anomaly detection benchmarks, OpenOOD (Yang et al., 2022) and ADBench (Han et al., 2022). We also show that the benefits of using OOD together with CP apply the other way around by using OOD scores as non-conformity scores, which results in improving upon current CP methods. One of the key messages of these contributions is that since OOD is concerned with designing scores and CP with interpreting these scores, the two fields may be inherently intertwined.