Improving Out-of-Distribution Detection by Combining Existing Post-hoc Methods

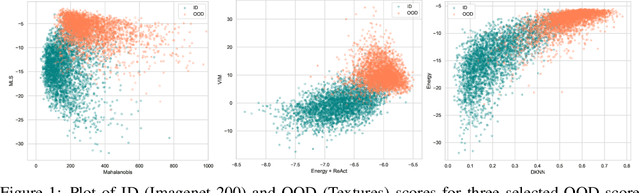
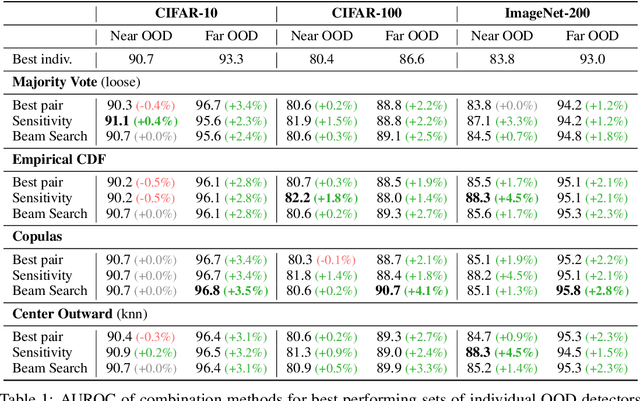
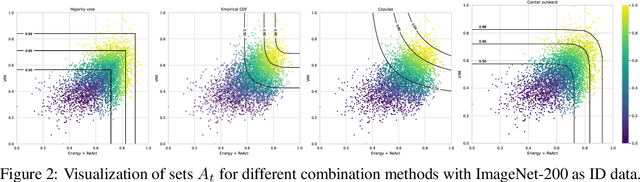
Since the seminal paper of Hendrycks et al. arXiv:1610.02136, Post-hoc deep Out-of-Distribution (OOD) detection has expanded rapidly. As a result, practitioners working on safety-critical applications and seeking to improve the robustness of a neural network now have a plethora of methods to choose from. However, no method outperforms every other on every dataset arXiv:2210.07242, so the current best practice is to test all the methods on the datasets at hand. This paper shifts focus from developing new methods to effectively combining existing ones to enhance OOD detection. We propose and compare four different strategies for integrating multiple detection scores into a unified OOD detector, based on techniques such as majority vote, empirical and copulas-based Cumulative Distribution Function modeling, and multivariate quantiles based on optimal transport. We extend common OOD evaluation metrics -- like AUROC and FPR at fixed TPR rates -- to these multi-dimensional OOD detectors, allowing us to evaluate them and compare them with individual methods on extensive benchmarks. Furthermore, we propose a series of guidelines to choose what OOD detectors to combine in more realistic settings, i.e. in the absence of known OOD data, relying on principles drawn from Outlier Exposure arXiv:1812.04606. The code is available at https://github.com/paulnovello/multi-ood.

Detecting Brittle Decisions for Free: Leveraging Margin Consistency in Deep Robust Classifiers

Despite extensive research on adversarial training strategies to improve robustness, the decisions of even the most robust deep learning models can still be quite sensitive to imperceptible perturbations, creating serious risks when deploying them for high-stakes real-world applications. While detecting such cases may be critical, evaluating a model's vulnerability at a per-instance level using adversarial attacks is computationally too intensive and unsuitable for real-time deployment scenarios. The input space margin is the exact score to detect non-robust samples and is intractable for deep neural networks. This paper introduces the concept of margin consistency -- a property that links the input space margins and the logit margins in robust models -- for efficient detection of vulnerable samples. First, we establish that margin consistency is a necessary and sufficient condition to use a model's logit margin as a score for identifying non-robust samples. Next, through comprehensive empirical analysis of various robustly trained models on CIFAR10 and CIFAR100 datasets, we show that they indicate strong margin consistency with a strong correlation between their input space margins and the logit margins. Then, we show that we can effectively use the logit margin to confidently detect brittle decisions with such models and accurately estimate robust accuracy on an arbitrarily large test set by estimating the input margins only on a small subset. Finally, we address cases where the model is not sufficiently margin-consistent by learning a pseudo-margin from the feature representation. Our findings highlight the potential of leveraging deep representations to efficiently assess adversarial vulnerability in deployment scenarios.

Layerwise Early Stopping for Test Time Adaptation

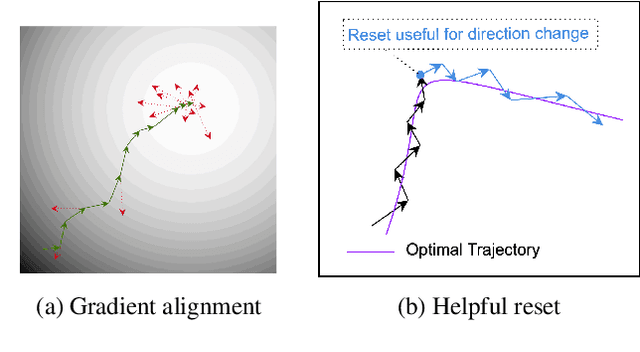
Test Time Adaptation (TTA) addresses the problem of distribution shift by enabling pretrained models to learn new features on an unseen domain at test time. However, it poses a significant challenge to maintain a balance between learning new features and retaining useful pretrained features. In this paper, we propose Layerwise EArly STopping (LEAST) for TTA to address this problem. The key idea is to stop adapting individual layers during TTA if the features being learned do not appear beneficial for the new domain. For that purpose, we propose using a novel gradient-based metric to measure the relevance of the current learnt features to the new domain without the need for supervised labels. More specifically, we propose to use this metric to determine dynamically when to stop updating each layer during TTA. This enables a more balanced adaptation, restricted to layers benefiting from it, and only for a certain number of steps. Such an approach also has the added effect of limiting the forgetting of pretrained features useful for dealing with new domains. Through extensive experiments, we demonstrate that Layerwise Early Stopping improves the performance of existing TTA approaches across multiple datasets, domain shifts, model architectures, and TTA losses.

GROOD: GRadient-aware Out-Of-Distribution detection in interpolated manifolds

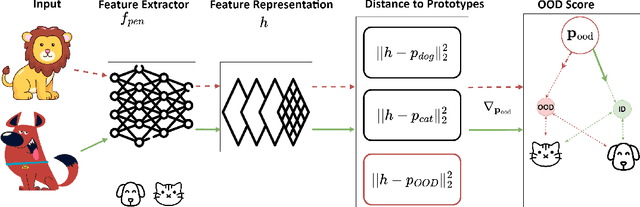
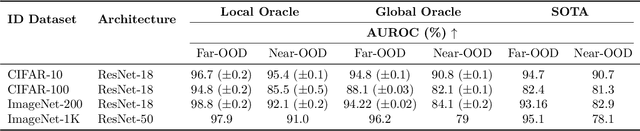
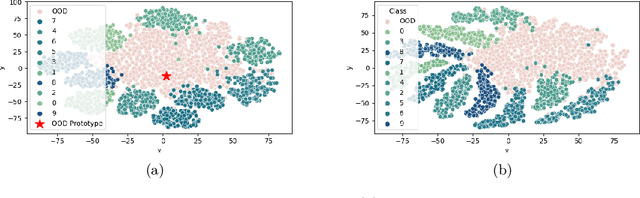
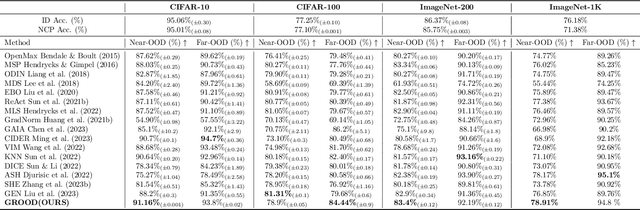
Deep neural networks (DNNs) often fail silently with over-confident predictions on out-of-distribution (OOD) samples, posing risks in real-world deployments. Existing techniques predominantly emphasize either the feature representation space or the gradient norms computed with respect to DNN parameters, yet they overlook the intricate gradient distribution and the topology of classification regions. To address this gap, we introduce GRadient-aware Out-Of-Distribution detection in interpolated manifolds (GROOD), a novel framework that relies on the discriminative power of gradient space to distinguish between in-distribution (ID) and OOD samples. To build this space, GROOD relies on class prototypes together with a prototype that specifically captures OOD characteristics. Uniquely, our approach incorporates a targeted mix-up operation at an early intermediate layer of the DNN to refine the separation of gradient spaces between ID and OOD samples. We quantify OOD detection efficacy using the distance to the nearest neighbor gradients derived from the training set, yielding a robust OOD score. Experimental evaluations substantiate that the introduction of targeted input mix-upamplifies the separation between ID and OOD in the gradient space, yielding impressive results across diverse datasets. Notably, when benchmarked against ImageNet-1k, GROOD surpasses the established robustness of state-of-the-art baselines. Through this work, we establish the utility of leveraging gradient spaces and class prototypes for enhanced OOD detection for DNN in image classification.

Understanding Interventional TreeSHAP : How and Why it Works

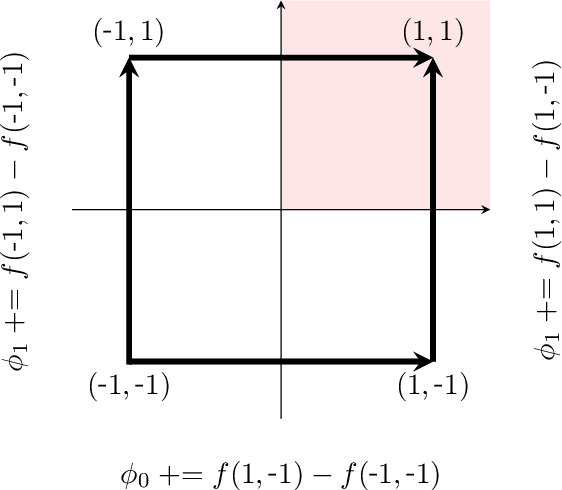
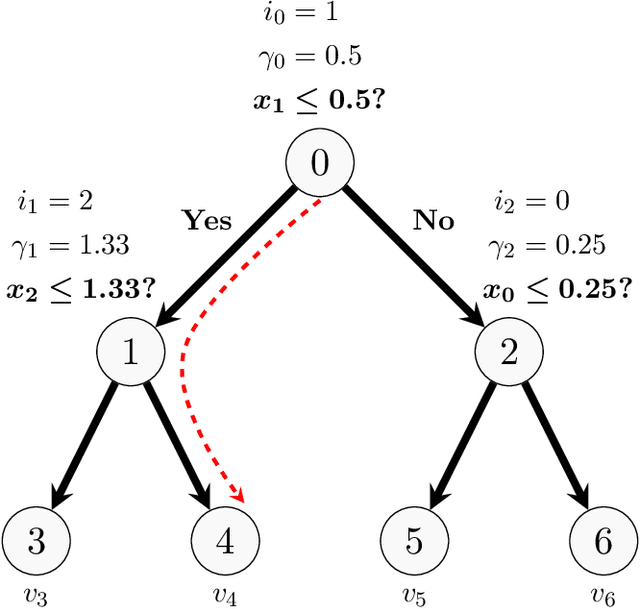
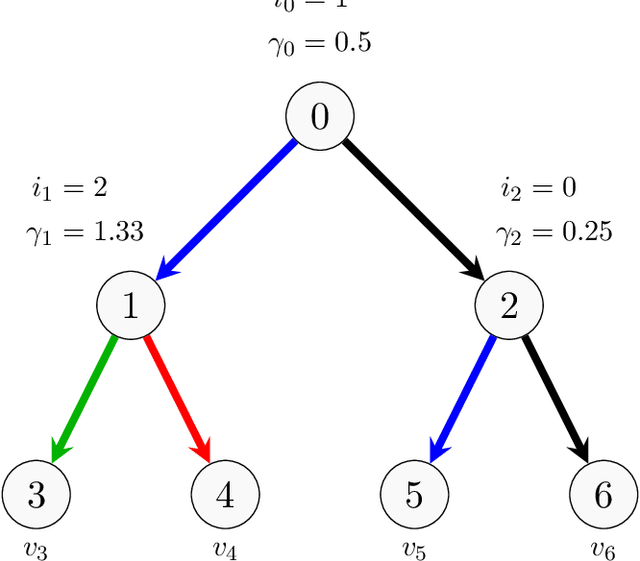
Shapley values are ubiquitous in interpretable Machine Learning due to their strong theoretical background and efficient implementation in the SHAP library. Computing these values used to induce an exponential cost with respect to the number of input features of an opaque model. Now, with efficient implementations such as Interventional TreeSHAP, this exponential burden is alleviated assuming one is explaining ensembles of decision trees. Although Interventional TreeSHAP has risen in popularity, it still lacks a formal proof of how/why it works. We provide such proof with the aim of not only increasing the transparency of the algorithm but also to encourage further development of these ideas. Notably, our proof for Interventional TreeSHAP is easily adapted to Shapley-Taylor indices.

Partial order: Finding Consensus among Uncertain Feature Attributions

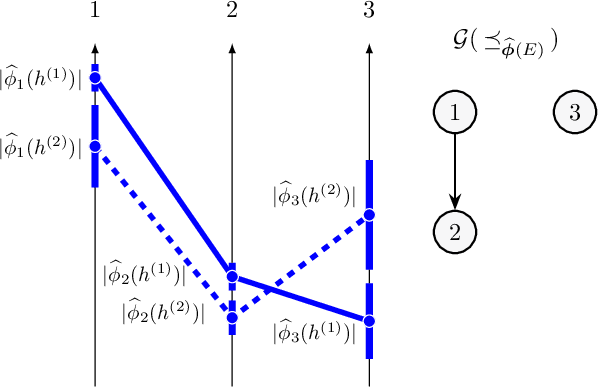
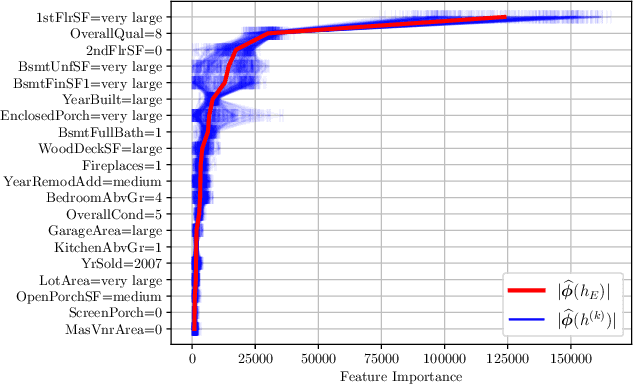
Post-hoc feature importance is progressively being employed to explain decisions of complex machine learning models. Yet in practice, reruns of the training algorithm and/or the explainer can result in contradicting statements of feature importance, henceforth reducing trust in those techniques. A possible avenue to address this issue is to develop strategies to aggregate diverse explanations about feature importance. While the arithmetic mean, which yields a total order, has been advanced, we introduce an alternative: the consensus among multiple models, which results in partial orders. The two aggregation strategies are compared using Integrated Gradients and Shapley values on two regression datasets, and we show that a large portion of the information provided by the mean aggregation is not supported by the consensus of each individual model, raising suspicion on the trustworthiness of this practice.

How to Certify Machine Learning Based Safety-critical Systems? A Systematic Literature Review

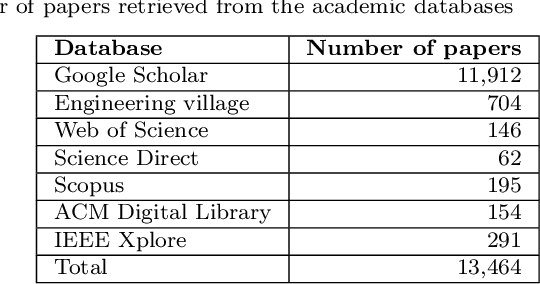
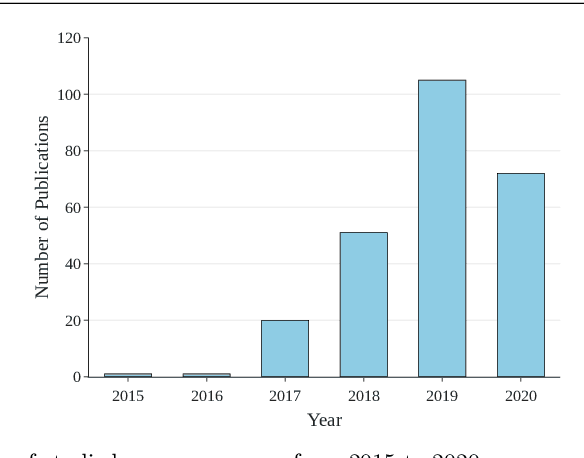
Context: Machine Learning (ML) has been at the heart of many innovations over the past years. However, including it in so-called 'safety-critical' systems such as automotive or aeronautic has proven to be very challenging, since the shift in paradigm that ML brings completely changes traditional certification approaches. Objective: This paper aims to elucidate challenges related to the certification of ML-based safety-critical systems, as well as the solutions that are proposed in the literature to tackle them, answering the question 'How to Certify Machine Learning Based Safety-critical Systems?'. Method: We conduct a Systematic Literature Review (SLR) of research papers published between 2015 to 2020, covering topics related to the certification of ML systems. In total, we identified 217 papers covering topics considered to be the main pillars of ML certification: Robustness, Uncertainty, Explainability, Verification, Safe Reinforcement Learning, and Direct Certification. We analyzed the main trends and problems of each sub-field and provided summaries of the papers extracted. Results: The SLR results highlighted the enthusiasm of the community for this subject, as well as the lack of diversity in terms of datasets and type of models. It also emphasized the need to further develop connections between academia and industries to deepen the domain study. Finally, it also illustrated the necessity to build connections between the above mention main pillars that are for now mainly studied separately. Conclusion: We highlighted current efforts deployed to enable the certification of ML based software systems, and discuss some future research directions.

Implicit Variational Inference: the Parameter and the Predictor Space

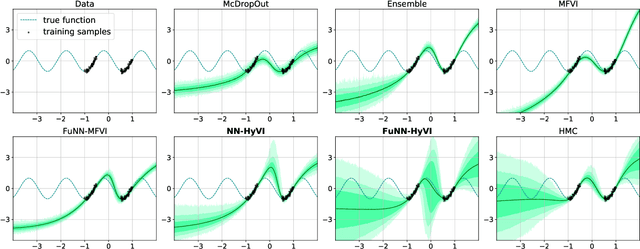
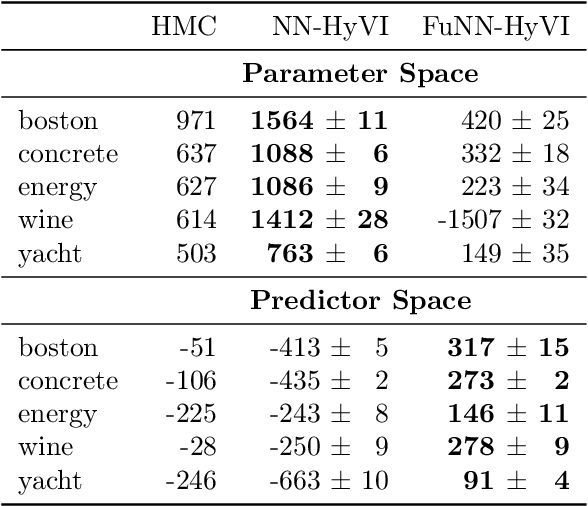
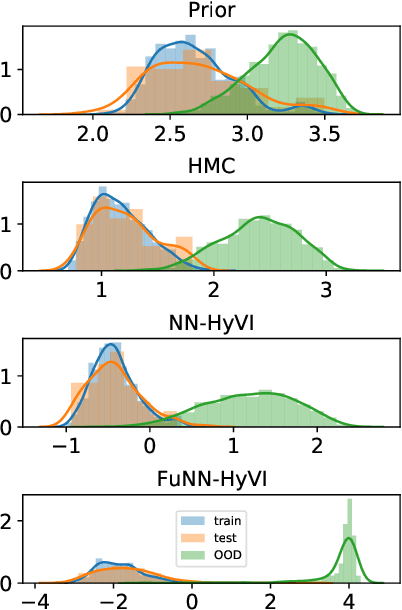
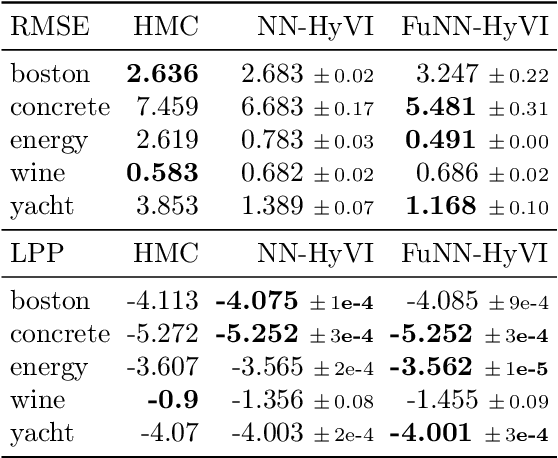
Having access to accurate confidence levels along with the predictions allows to determine whether making a decision is worth the risk. Under the Bayesian paradigm, the posterior distribution over parameters is used to capture model uncertainty, a valuable information that can be translated into predictive uncertainty. However, computing the posterior distribution for high capacity predictors, such as neural networks, is generally intractable, making approximate methods such as variational inference a promising alternative. While most methods perform inference in the space of parameters, we explore the benefits of carrying inference directly in the space of predictors. Relying on a family of distributions given by a deep generative neural network, we present two ways of carrying variational inference: one in \emph{parameter space}, one in \emph{predictor space}. Importantly, the latter requires us to choose a distribution of inputs, therefore allowing us at the same time to explicitly address the question of \emph{out-of-distribution} uncertainty. We explore from various perspectives the implications of working in the predictor space induced by neural networks as opposed to the parameter space, focusing mainly on the quality of uncertainty estimation for data lying outside of the training distribution. We compare posterior approximations obtained with these two methods to several standard methods and present results showing that variational approximations learned in the predictor space distinguish themselves positively from those trained in the parameter space.