Implicit Variational Inference: the Parameter and the Predictor Space

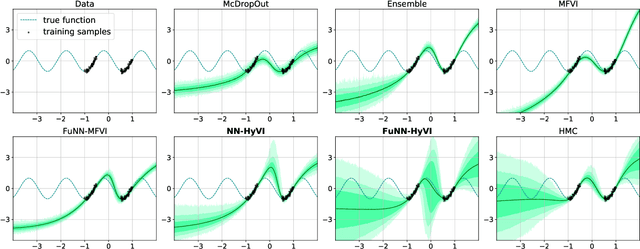
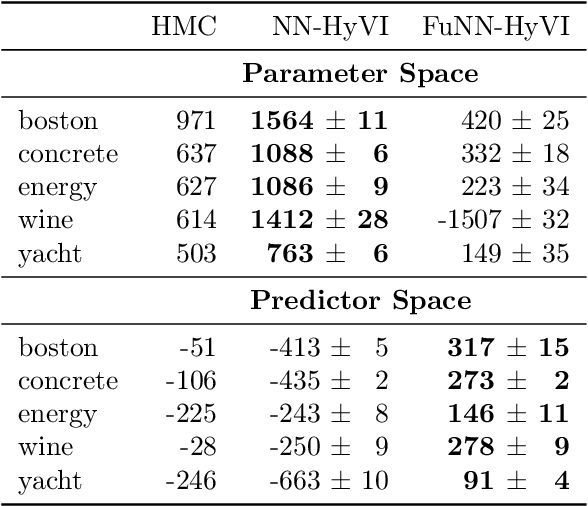
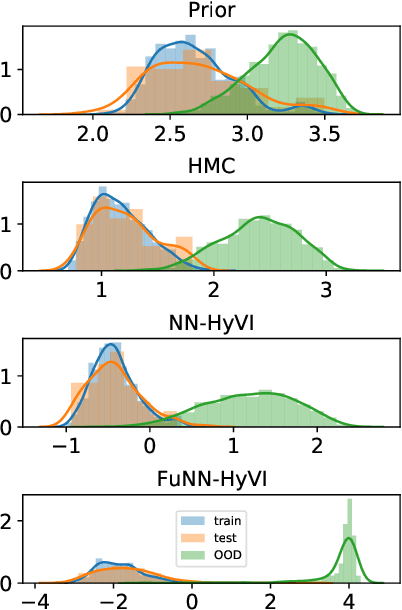
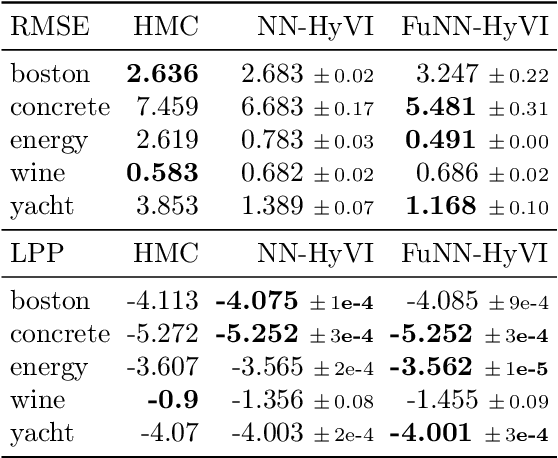
Having access to accurate confidence levels along with the predictions allows to determine whether making a decision is worth the risk. Under the Bayesian paradigm, the posterior distribution over parameters is used to capture model uncertainty, a valuable information that can be translated into predictive uncertainty. However, computing the posterior distribution for high capacity predictors, such as neural networks, is generally intractable, making approximate methods such as variational inference a promising alternative. While most methods perform inference in the space of parameters, we explore the benefits of carrying inference directly in the space of predictors. Relying on a family of distributions given by a deep generative neural network, we present two ways of carrying variational inference: one in \emph{parameter space}, one in \emph{predictor space}. Importantly, the latter requires us to choose a distribution of inputs, therefore allowing us at the same time to explicitly address the question of \emph{out-of-distribution} uncertainty. We explore from various perspectives the implications of working in the predictor space induced by neural networks as opposed to the parameter space, focusing mainly on the quality of uncertainty estimation for data lying outside of the training distribution. We compare posterior approximations obtained with these two methods to several standard methods and present results showing that variational approximations learned in the predictor space distinguish themselves positively from those trained in the parameter space.