Implicit Variational Inference: the Parameter and the Predictor Space

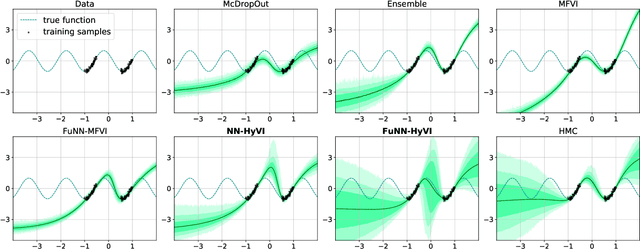
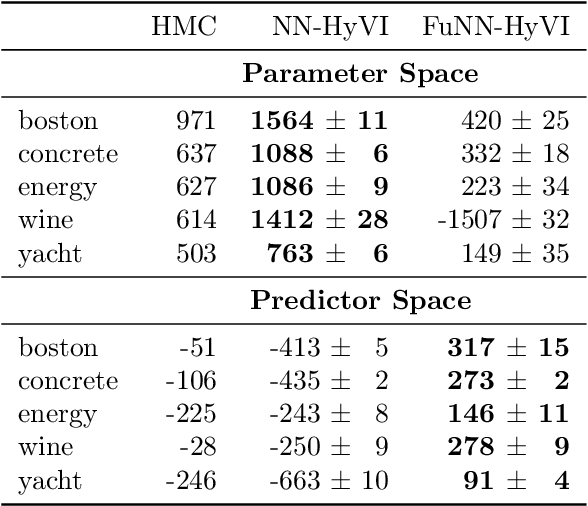
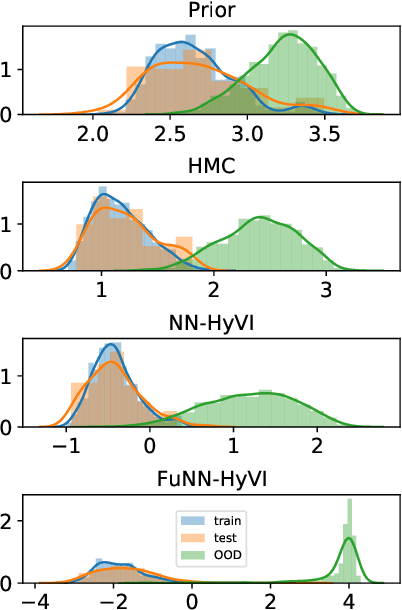
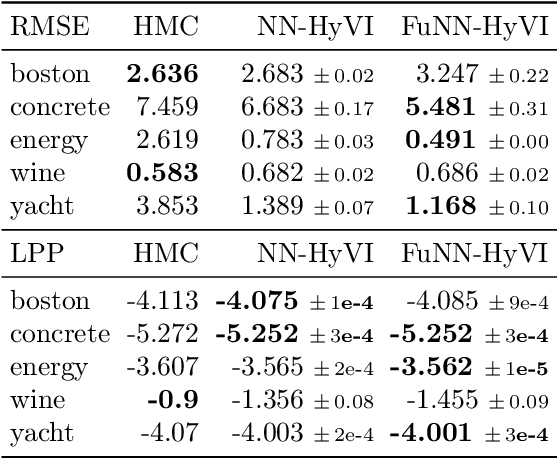
Having access to accurate confidence levels along with the predictions allows to determine whether making a decision is worth the risk. Under the Bayesian paradigm, the posterior distribution over parameters is used to capture model uncertainty, a valuable information that can be translated into predictive uncertainty. However, computing the posterior distribution for high capacity predictors, such as neural networks, is generally intractable, making approximate methods such as variational inference a promising alternative. While most methods perform inference in the space of parameters, we explore the benefits of carrying inference directly in the space of predictors. Relying on a family of distributions given by a deep generative neural network, we present two ways of carrying variational inference: one in \emph{parameter space}, one in \emph{predictor space}. Importantly, the latter requires us to choose a distribution of inputs, therefore allowing us at the same time to explicitly address the question of \emph{out-of-distribution} uncertainty. We explore from various perspectives the implications of working in the predictor space induced by neural networks as opposed to the parameter space, focusing mainly on the quality of uncertainty estimation for data lying outside of the training distribution. We compare posterior approximations obtained with these two methods to several standard methods and present results showing that variational approximations learned in the predictor space distinguish themselves positively from those trained in the parameter space.

The Indian Chefs Process

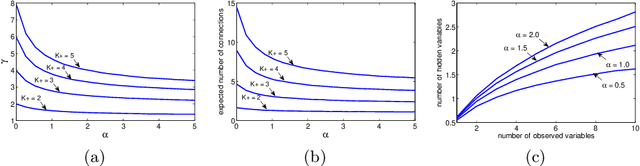
This paper introduces the Indian Chefs Process (ICP), a Bayesian nonparametric prior on the joint space of infinite directed acyclic graphs (DAGs) and orders that generalizes Indian Buffet Processes. As our construction shows, the proposed distribution relies on a latent Beta Process controlling both the orders and outgoing connection probabilities of the nodes, and yields a probability distribution on sparse infinite graphs. The main advantage of the ICP over previously proposed Bayesian nonparametric priors for DAG structures is its greater flexibility. To the best of our knowledge, the ICP is the first Bayesian nonparametric model supporting every possible DAG. We demonstrate the usefulness of the ICP on learning the structure of deep generative sigmoid networks as well as convolutional neural networks.

Tree bark re-identification using a deep-learning feature descriptor

The ability to visually re-identify objects is a fundamental capability in vision systems. Oftentimes, it relies on collections of visual signatures based on descriptors, such as Scale Invariant Feature Transform (SIFT) or Speeded Up Robust Features (SURF). However, these traditional descriptors were designed for a certain domain of surface appearances and geometries (limited relief). Consequently, highly-textured surfaces such as tree bark pose a challenge to them. In turns, this makes it more difficult to use trees as identifiable landmarks for navigational purposes (robotics) or to track felled lumber along a supply chain (logistics). We thus propose to use data-driven descriptors trained on bark images for tree surface re-identification. To this effect, we collected a large dataset containing 2,400 bark images with strong illumination changes, annotated by surface and with the ability to pixel-align them. We used this dataset to sample from more than 2 million 64x64 pixel patches to train our novel local descriptors DeepBark and SqueezeBark. Our DeepBark method has shown a clear advantage against the hand-crafted descriptors SIFT and SURF. Furthermore, we demonstrated that DeepBark can reach a Precision@1 of 99.8% in a database of 7,900 images with only 11 relevant images. Our work thus suggests that re-identifying tree surfaces in a challenging context is possible, while making public a new dataset.