Probabilistic Pontryagin's Maximum Principle for Continuous-Time Model-Based Reinforcement Learning

Without exact knowledge of the true system dynamics, optimal control of non-linear continuous-time systems requires careful treatment of epistemic uncertainty. In this work, we propose a probabilistic extension to Pontryagin's maximum principle by minimizing the mean Hamiltonian with respect to epistemic uncertainty. We show minimization of the mean Hamiltonian is a necessary optimality condition when optimizing the mean cost, and propose a multiple shooting numerical method scalable to large-scale probabilistic dynamical models, including ensemble neural ordinary differential equations. Comparisons against state-of-the-art methods in online and offline model-based reinforcement learning tasks show that our probabilistic Hamiltonian formulation leads to reduced trial costs in offline settings and achieves competitive performance in online scenarios. By bridging optimal control and reinforcement learning, our approach offers a principled and practical framework for controlling uncertain systems with learned dynamics.

Robust Inference of Dynamic Covariance Using Wishart Processes and Sequential Monte Carlo

Several disciplines, such as econometrics, neuroscience, and computational psychology, study the dynamic interactions between variables over time. A Bayesian nonparametric model known as the Wishart process has been shown to be effective in this situation, but its inference remains highly challenging. In this work, we introduce a Sequential Monte Carlo (SMC) sampler for the Wishart process, and show how it compares to conventional inference approaches, namely MCMC and variational inference. Using simulations we show that SMC sampling results in the most robust estimates and out-of-sample predictions of dynamic covariance. SMC especially outperforms the alternative approaches when using composite covariance functions with correlated parameters. We demonstrate the practical applicability of our proposed approach on a dataset of clinical depression (n=1), and show how using an accurate representation of the posterior distribution can be used to test for dynamics on covariance

Automatic structured variational inference

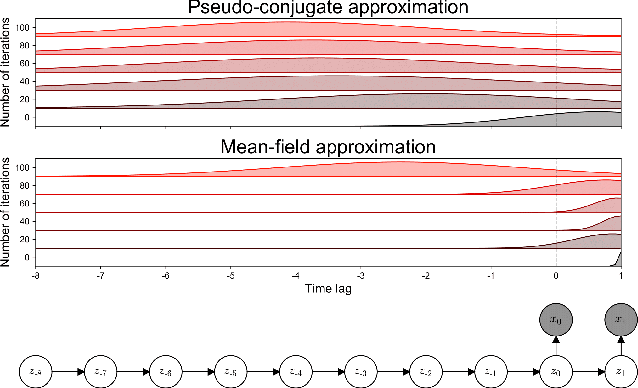
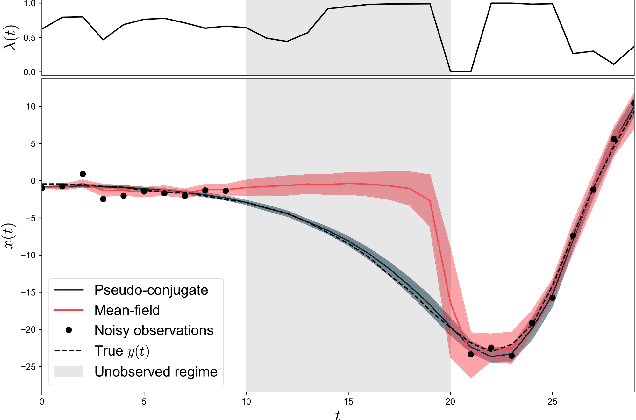
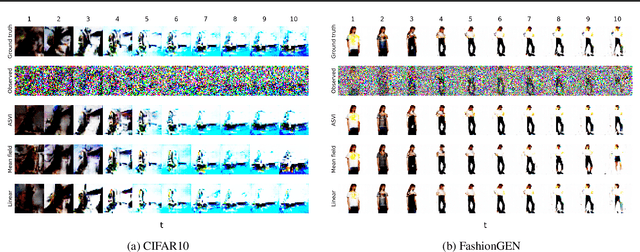
The aim of probabilistic programming is to automatize every aspect of probabilistic inference in arbitrary probabilistic models (programs) so that the user can focus her attention on modeling, without dealing with ad-hoc inference methods. Gradient based automatic differentiation stochastic variational inference offers an attractive option as the default method for (differentiable) probabilistic programming as it combines high performance with high computational efficiency. However, the performance of any (parametric) variational approach depends on the choice of an appropriate variational family. Here, we introduced a fully automatic method for constructing structured variational families inspired to the closed-form update in conjugate models. These pseudo-conjugate families incorporate the forward pass of the input probabilistic program and can capture complex statistical dependencies. Pseudo-conjugate families have the same space and time complexity of the input probabilistic program and are therefore tractable in a very large class of models. We validate our automatic variational method on a wide range of high dimensional inference problems including deep learning components.

The Indian Chefs Process

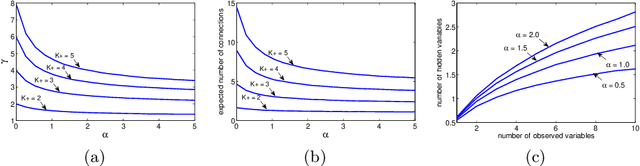
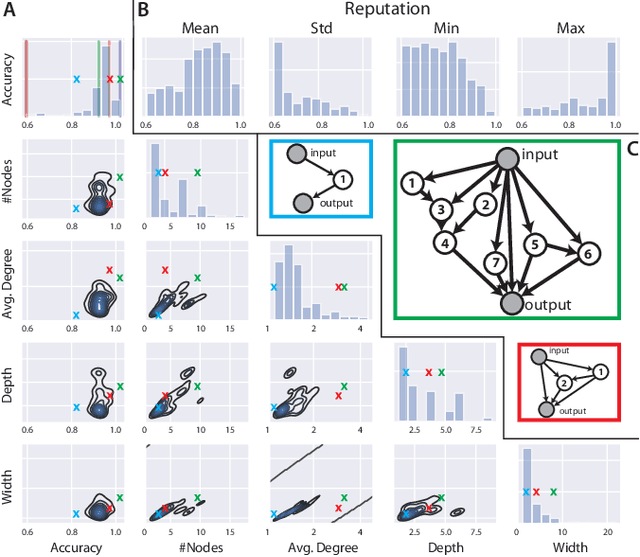
This paper introduces the Indian Chefs Process (ICP), a Bayesian nonparametric prior on the joint space of infinite directed acyclic graphs (DAGs) and orders that generalizes Indian Buffet Processes. As our construction shows, the proposed distribution relies on a latent Beta Process controlling both the orders and outgoing connection probabilities of the nodes, and yields a probability distribution on sparse infinite graphs. The main advantage of the ICP over previously proposed Bayesian nonparametric priors for DAG structures is its greater flexibility. To the best of our knowledge, the ICP is the first Bayesian nonparametric model supporting every possible DAG. We demonstrate the usefulness of the ICP on learning the structure of deep generative sigmoid networks as well as convolutional neural networks.

Causal inference using Bayesian non-parametric quasi-experimental design

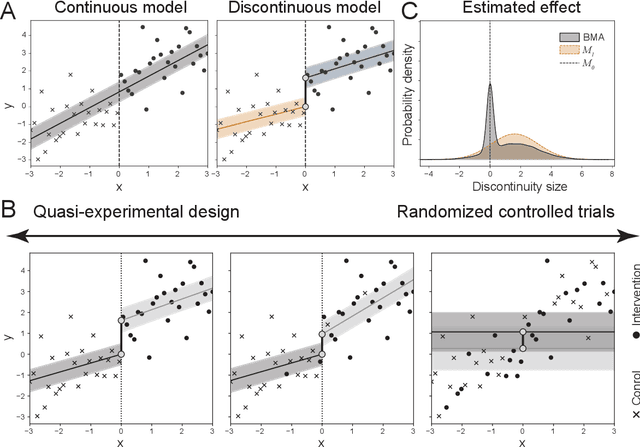
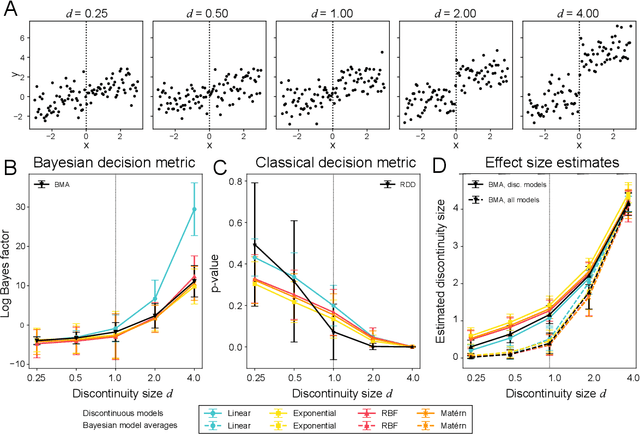
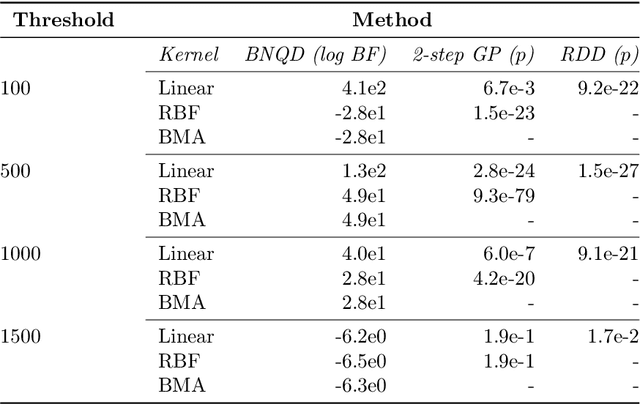
The de facto standard for causal inference is the randomized controlled trial, where one compares an manipulated group with a control group in order to determine the effect of an intervention. However, this research design is not always realistically possible due to pragmatic or ethical concerns. In these situations, quasi-experimental designs may provide a solution, as these allow for causal conclusions at the cost of additional design assumptions. In this paper, we provide a generic framework for quasi-experimental design using Bayesian model comparison, and we show how it can be used as an alternative to several common research designs. We provide a theoretical motivation for a Gaussian process based approach and demonstrate its convenient use in a number of simulations. Finally, we apply the framework to determine the effect of population-based thresholds for municipality funding in France, of the 2005 smoking ban in Sicily on the number of acute coronary events, and of the effect of an alleged historical phantom border in the Netherlands on Dutch voting behaviour.

Wasserstein Variational Inference

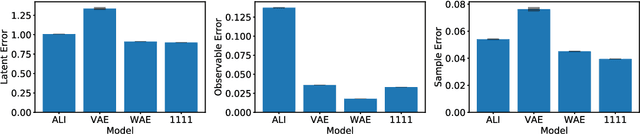
This paper introduces Wasserstein variational inference, a new form of approximate Bayesian inference based on optimal transport theory. Wasserstein variational inference uses a new family of divergences that includes both f-divergences and the Wasserstein distance as special cases. The gradients of the Wasserstein variational loss are obtained by backpropagating through the Sinkhorn iterations. This technique results in a very stable likelihood-free training method that can be used with implicit distributions and probabilistic programs. Using the Wasserstein variational inference framework, we introduce several new forms of autoencoders and test their robustness and performance against existing variational autoencoding techniques.

Forward Amortized Inference for Likelihood-Free Variational Marginalization

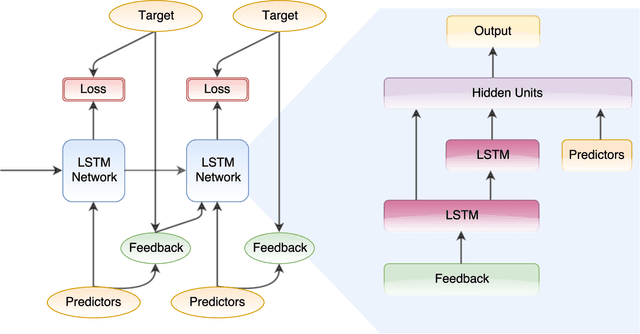
In this paper, we introduce a new form of amortized variational inference by using the forward KL divergence in a joint-contrastive variational loss. The resulting forward amortized variational inference is a likelihood-free method as its gradient can be sampled without bias and without requiring any evaluation of either the model joint distribution or its derivatives. We prove that our new variational loss is optimized by the exact posterior marginals in the fully factorized mean-field approximation, a property that is not shared with the more conventional reverse KL inference. Furthermore, we show that forward amortized inference can be easily marginalized over large families of latent variables in order to obtain a marginalized variational posterior. We consider two examples of variational marginalization. In our first example we train a Bayesian forecaster for predicting a simplified chaotic model of atmospheric convection. In the second example we train an amortized variational approximation of a Bayesian optimal classifier by marginalizing over the model space. The result is a powerful meta-classification network that can solve arbitrary classification problems without further training.

GP CaKe: Effective brain connectivity with causal kernels

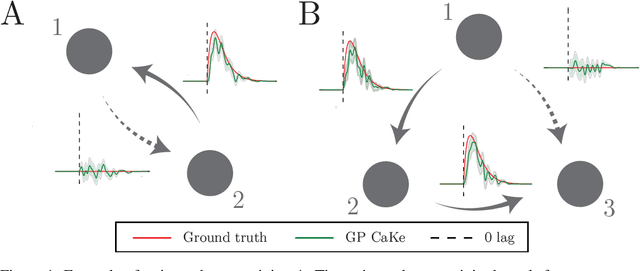
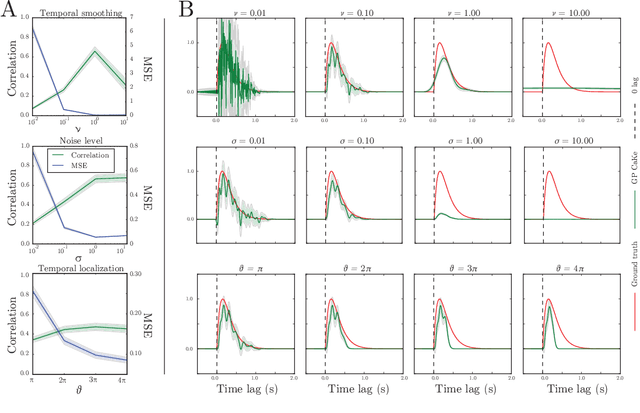
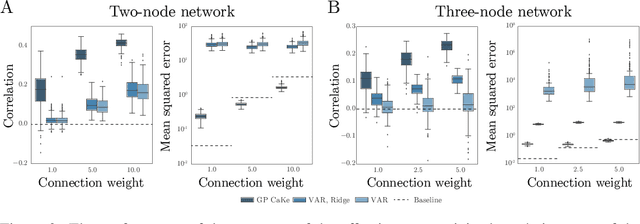
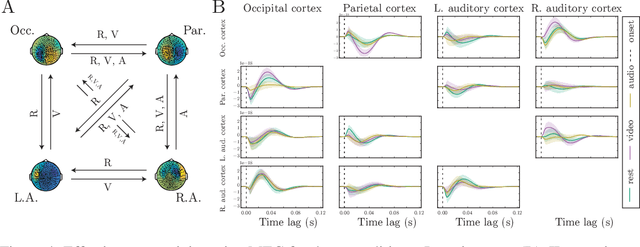
A fundamental goal in network neuroscience is to understand how activity in one region drives activity elsewhere, a process referred to as effective connectivity. Here we propose to model this causal interaction using integro-differential equations and causal kernels that allow for a rich analysis of effective connectivity. The approach combines the tractability and flexibility of autoregressive modeling with the biophysical interpretability of dynamic causal modeling. The causal kernels are learned nonparametrically using Gaussian process regression, yielding an efficient framework for causal inference. We construct a novel class of causal covariance functions that enforce the desired properties of the causal kernels, an approach which we call GP CaKe. By construction, the model and its hyperparameters have biophysical meaning and are therefore easily interpretable. We demonstrate the efficacy of GP CaKe on a number of simulations and give an example of a realistic application on magnetoencephalography (MEG) data.