Probabilistic Pontryagin's Maximum Principle for Continuous-Time Model-Based Reinforcement Learning

Without exact knowledge of the true system dynamics, optimal control of non-linear continuous-time systems requires careful treatment of epistemic uncertainty. In this work, we propose a probabilistic extension to Pontryagin's maximum principle by minimizing the mean Hamiltonian with respect to epistemic uncertainty. We show minimization of the mean Hamiltonian is a necessary optimality condition when optimizing the mean cost, and propose a multiple shooting numerical method scalable to large-scale probabilistic dynamical models, including ensemble neural ordinary differential equations. Comparisons against state-of-the-art methods in online and offline model-based reinforcement learning tasks show that our probabilistic Hamiltonian formulation leads to reduced trial costs in offline settings and achieves competitive performance in online scenarios. By bridging optimal control and reinforcement learning, our approach offers a principled and practical framework for controlling uncertain systems with learned dynamics.

Early-Cycle Internal Impedance Enables ML-Based Battery Cycle Life Predictions Across Manufacturers

Predicting the end-of-life (EOL) of lithium-ion batteries across different manufacturers presents significant challenges due to variations in electrode materials, manufacturing processes, cell formats, and a lack of generally available data. Methods that construct features solely on voltage-capacity profile data typically fail to generalize across cell chemistries. This study introduces a methodology that combines traditional voltage-capacity features with Direct Current Internal Resistance (DCIR) measurements, enabling more accurate and generalizable EOL predictions. The use of early-cycle DCIR data captures critical degradation mechanisms related to internal resistance growth, enhancing model robustness. Models are shown to successfully predict the number of cycles to EOL for unseen manufacturers of varied electrode composition with a mean absolute error (MAE) of 150 cycles. This cross-manufacturer generalizability reduces the need for extensive new data collection and retraining, enabling manufacturers to optimize new battery designs using existing datasets. Additionally, a novel DCIR-compatible dataset is released as part of ongoing efforts to enrich the growing ecosystem of cycling data and accelerate battery materials development.

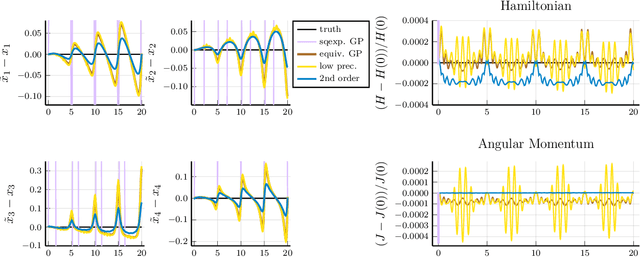
Discrete Lagrangian Neural Networks with Automatic Symmetry Discovery

By one of the most fundamental principles in physics, a dynamical system will exhibit those motions which extremise an action functional. This leads to the formation of the Euler-Lagrange equations, which serve as a model of how the system will behave in time. If the dynamics exhibit additional symmetries, then the motion fulfils additional conservation laws, such as conservation of energy (time invariance), momentum (translation invariance), or angular momentum (rotational invariance). To learn a system representation, one could learn the discrete Euler-Lagrange equations, or alternatively, learn the discrete Lagrangian function $\mathcal{L}_d$ which defines them. Based on ideas from Lie group theory, in this work we introduce a framework to learn a discrete Lagrangian along with its symmetry group from discrete observations of motions and, therefore, identify conserved quantities. The learning process does not restrict the form of the Lagrangian, does not require velocity or momentum observations or predictions and incorporates a cost term which safeguards against unwanted solutions and against potential numerical issues in forward simulations. The learnt discrete quantities are related to their continuous analogues using variational backward error analysis and numerical results demonstrate the improvement such models can have both qualitatively and quantitatively even in the presence of noise.

Approximate Uncertainty Propagation for Continuous Gaussian Process Dynamical Systems

When learning continuous dynamical systems with Gaussian Processes, computing trajectories requires repeatedly mapping the distributions of uncertain states through the distribution of learned nonlinear functions, which is generally intractable. Since sampling-based approaches are computationally expensive, we consider approximations of the output and trajectory distributions. We show that existing methods make an incorrect implicit independence assumption and underestimate the model-induced uncertainty. We propose a piecewise linear approximation of the GP model yielding a class of numerical solvers for efficient uncertainty estimates matching sampling-based methods.

Learning ODE Models with Qualitative Structure Using Gaussian Processes

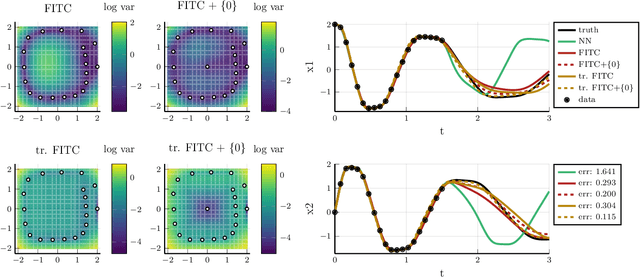
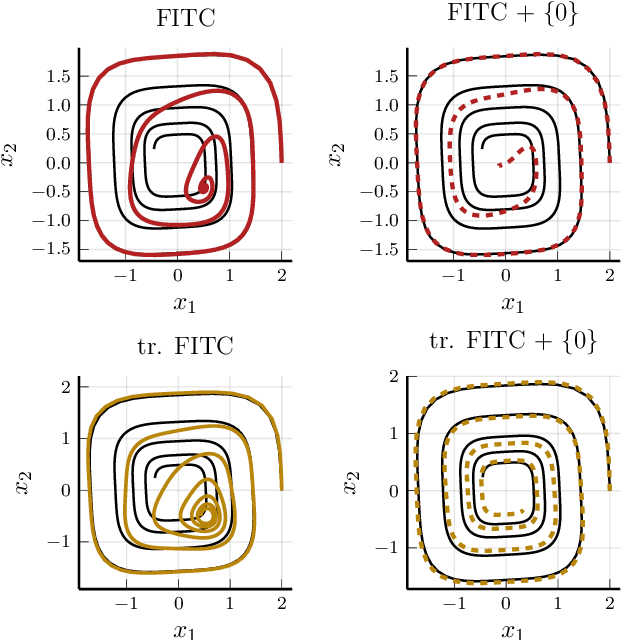
Recent advances in learning techniques have enabled the modelling of dynamical systems for scientific and engineering applications directly from data. However, in many contexts, explicit data collection is expensive and learning algorithms must be data-efficient to be feasible. This suggests using additional qualitative information about the system, which is often available from prior experiments or domain knowledge. In this paper, we propose an approach to learning the vector field of differential equations using sparse Gaussian Processes that allows us to combine data and additional structural information, like Lie Group symmetries and fixed points, as well as known input transformations. We show that this combination improves extrapolation performance and long-term behaviour significantly, while also reducing the computational cost.