Learning ODE Models with Qualitative Structure Using Gaussian Processes

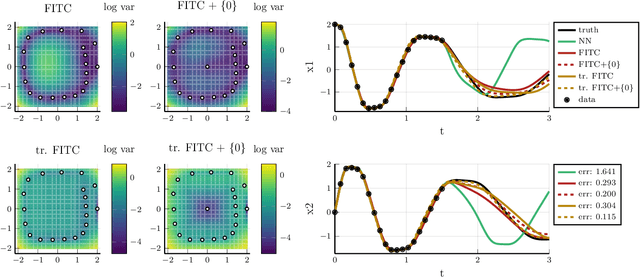
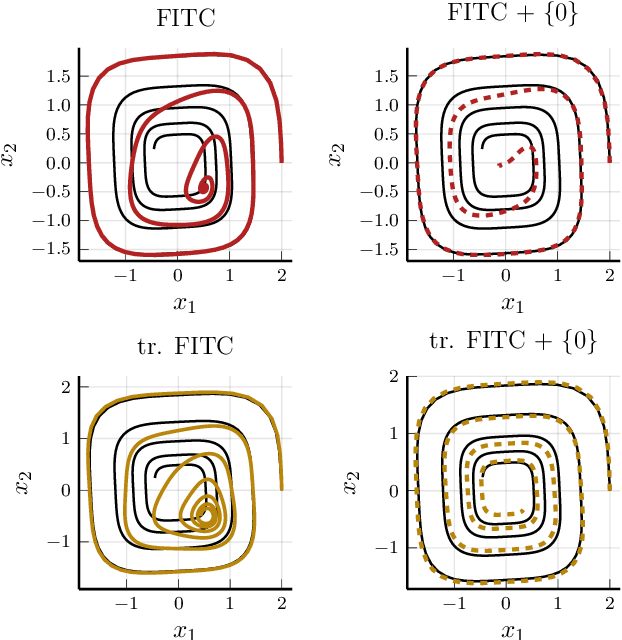
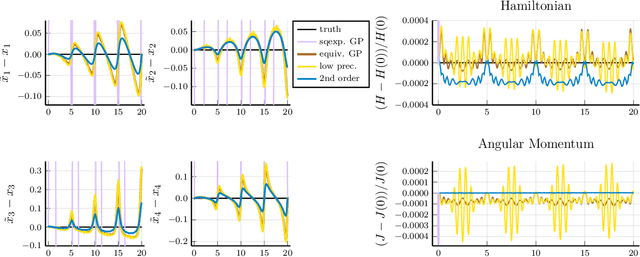
Recent advances in learning techniques have enabled the modelling of dynamical systems for scientific and engineering applications directly from data. However, in many contexts, explicit data collection is expensive and learning algorithms must be data-efficient to be feasible. This suggests using additional qualitative information about the system, which is often available from prior experiments or domain knowledge. In this paper, we propose an approach to learning the vector field of differential equations using sparse Gaussian Processes that allows us to combine data and additional structural information, like Lie Group symmetries and fixed points, as well as known input transformations. We show that this combination improves extrapolation performance and long-term behaviour significantly, while also reducing the computational cost.