Beyond Benchmarks: A Novel Framework for Domain-Specific LLM Evaluation and Knowledge Mapping

The paper addresses two critical challenges in language model (LM) evaluation: creating reliable domain-specific benchmarks and understanding knowledge representation during domain adaptation. We introduce a deterministic pipeline that converts raw domain corpora into completion-type benchmarks without relying on LMs or human curation, eliminating benchmark contamination issues while enabling evaluation on the latest domain data. Our approach generates domain-specific keywords and related word lists using TF and Term TF-IDF methods and constructs prompt-target pairs. We evaluate models by measuring their ability to complete these prompts with the correct domain-specific targets, providing a direct assessment of domain knowledge with low computational cost. Through comprehensive experiments across multiple models (GPT-2 medium/XL, Llama-2/3.1, OLMo-2, Qwen-2, Mistral) and domains, we demonstrate that our benchmark strongly correlates with expert-generated benchmarks while providing a more accurate measure of domain knowledge than traditional perplexity metrics. We reveal that domain adaptation happens rapidly in smaller models (within 500 steps) and illustrate a new approach to domain knowledge evaluation in base models during training for early stopping. By extending mechanistic analysis to domain adaptation, we discover that initial-to-mid layers are primarily responsible for attribute extraction, while later layers focus on next token prediction. Furthermore, we show that during adaptation, forgetting begins in the middle layers, where attribute extraction happens and is amplified in later layers. Our work provides both a practical evaluation methodology for domain-specific LMs and novel insights into knowledge representation during adaptation, with implications for more efficient fine-tuning strategies and targeted approaches to mitigate catastrophic forgetting.

Question Answering under Temporal Conflict: Evaluating and Organizing Evolving Knowledge with LLMs

Large language models (LLMs) exhibit remarkable capabilities in question answering and reasoning thanks to their extensive parametric memory. However, their knowledge is inherently limited by the scope of their pre-training data, while real-world information evolves continuously. Updating this knowledge typically requires costly and brittle re-training, or in-context learning (ICL), which becomes impractical at scale given the volume and volatility of modern information. Motivated by these limitations, we investigate how LLMs perform when exposed to temporal text corpora, or documents that reflect evolving knowledge over time, such as sports biographies where facts like a player's "current team" change year by year. To this end, we introduce two new benchmarks: Temporal Wiki, which captures factual drift across historical Wikipedia snapshots, and Unified Clark, which aggregates timestamped news articles to simulate real-world information accumulation. Our analysis reveals that LLMs often struggle to reconcile conflicting or outdated facts and can be misled when multiple versions of a fact appear in context. To address these issues, we propose a lightweight, agentic framework that incrementally builds a structured, external memory from source documents without requiring re-training. This knowledge organization strategy enables models to retrieve and reason over temporally filtered, relevant information at inference time. Empirically, our method outperforms ICL and RAG baselines across both benchmarks, especially on questions requiring more complex reasoning or integration of conflicting facts.

Object-level Self-Distillation for Vision Pretraining

State-of-the-art vision pretraining methods rely on image-level self-distillation from object-centric datasets such as ImageNet, implicitly assuming each image contains a single object. This assumption does not always hold: many ImageNet images already contain multiple objects. Further, it limits scalability to scene-centric datasets that better mirror real-world complexity. We address these challenges by introducing Object-level Self-DIStillation (ODIS), a pretraining approach that shifts the self-distillation granularity from whole images to individual objects. Using object-aware cropping and masked attention, ODIS isolates object-specific regions, guiding the transformer toward semantically meaningful content and transforming a noisy, scene-level task into simpler object-level sub-tasks. We show that this approach improves visual representations both at the image and patch levels. Using masks at inference time, our method achieves an impressive $82.6\%$ $k$-NN accuracy on ImageNet1k with ViT-Large.

A Reproduction Study: The Kernel PCA Interpretation of Self-Attention Fails Under Scrutiny

In this reproduction study, we revisit recent claims that self-attention implements kernel principal component analysis (KPCA) (Teo et al., 2024), positing that (i) value vectors $V$ capture the eigenvectors of the Gram matrix of the keys, and (ii) that self-attention projects queries onto the principal component axes of the key matrix $K$ in a feature space. Our analysis reveals three critical inconsistencies: (1) No alignment exists between learned self-attention value vectors and what is proposed in the KPCA perspective, with average similarity metrics (optimal cosine similarity $\leq 0.32$, linear CKA (Centered Kernel Alignment) $\leq 0.11$, kernel CKA $\leq 0.32$) indicating negligible correspondence; (2) Reported decreases in reconstruction loss $J_\text{proj}$, arguably justifying the claim that the self-attention minimizes the projection error of KPCA, are misinterpreted, as the quantities involved differ by orders of magnitude ($\sim\!10^3$); (3) Gram matrix eigenvalue statistics, introduced to justify that $V$ captures the eigenvector of the gram matrix, are irreproducible without undocumented implementation-specific adjustments. Across 10 transformer architectures, we conclude that the KPCA interpretation of self-attention lacks empirical support.

Probabilistic Pontryagin's Maximum Principle for Continuous-Time Model-Based Reinforcement Learning

Without exact knowledge of the true system dynamics, optimal control of non-linear continuous-time systems requires careful treatment of epistemic uncertainty. In this work, we propose a probabilistic extension to Pontryagin's maximum principle by minimizing the mean Hamiltonian with respect to epistemic uncertainty. We show minimization of the mean Hamiltonian is a necessary optimality condition when optimizing the mean cost, and propose a multiple shooting numerical method scalable to large-scale probabilistic dynamical models, including ensemble neural ordinary differential equations. Comparisons against state-of-the-art methods in online and offline model-based reinforcement learning tasks show that our probabilistic Hamiltonian formulation leads to reduced trial costs in offline settings and achieves competitive performance in online scenarios. By bridging optimal control and reinforcement learning, our approach offers a principled and practical framework for controlling uncertain systems with learned dynamics.

Adaptation Odyssey in LLMs: Why Does Additional Pretraining Sometimes Fail to Improve?

In the last decade, the generalization and adaptation abilities of deep learning models were typically evaluated on fixed training and test distributions. Contrary to traditional deep learning, large language models (LLMs) are (i) even more overparameterized, (ii) trained on unlabeled text corpora curated from the Internet with minimal human intervention, and (iii) trained in an online fashion. These stark contrasts prevent researchers from transferring lessons learned on model generalization and adaptation in deep learning contexts to LLMs. To this end, our short paper introduces empirical observations that aim to shed light on further training of already pretrained language models. Specifically, we demonstrate that training a model on a text domain could degrade its perplexity on the test portion of the same domain. We observe with our subsequent analysis that the performance degradation is positively correlated with the similarity between the additional and the original pretraining dataset of the LLM. Our further token-level perplexity observations reveals that the perplexity degradation is due to a handful of tokens that are not informative about the domain. We hope these findings will guide us in determining when to adapt a model vs when to rely on its foundational capabilities.

Identifying latent state transition in non-linear dynamical systems

This work aims to improve generalization and interpretability of dynamical systems by recovering the underlying lower-dimensional latent states and their time evolutions. Previous work on disentangled representation learning within the realm of dynamical systems focused on the latent states, possibly with linear transition approximations. As such, they cannot identify nonlinear transition dynamics, and hence fail to reliably predict complex future behavior. Inspired by the advances in nonlinear ICA, we propose a state-space modeling framework in which we can identify not just the latent states but also the unknown transition function that maps the past states to the present. We introduce a practical algorithm based on variational auto-encoders and empirically demonstrate in realistic synthetic settings that we can (i) recover latent state dynamics with high accuracy, (ii) correspondingly achieve high future prediction accuracy, and (iii) adapt fast to new environments.

Investigating Continual Pretraining in Large Language Models: Insights and Implications

This paper studies the evolving domain of Continual Learning (CL) in large language models (LLMs), with a focus on developing strategies for efficient and sustainable training. Our primary emphasis is on continual domain-adaptive pretraining, a process designed to equip LLMs with the ability to integrate new information from various domains while retaining previously learned knowledge and enhancing cross-domain knowledge transfer without relying on domain-specific identification. Unlike previous studies, which mostly concentrate on a limited selection of tasks or domains and primarily aim to address the issue of forgetting, our research evaluates the adaptability and capabilities of LLMs to changing data landscapes in practical scenarios. To this end, we introduce a new benchmark designed to measure the adaptability of LLMs to these evolving data environments, offering a comprehensive framework for evaluation. We examine the impact of model size on learning efficacy and forgetting, as well as how the progression and similarity of emerging domains affect the knowledge transfer within these models. Our findings uncover several key insights: (i) when the sequence of domains shows semantic similarity, continual pretraining enables LLMs to better specialize in the current domain compared to stand-alone fine-tuning, (ii) training across a diverse range of domains enhances both backward and forward knowledge transfer, and (iii) smaller models are particularly sensitive to continual pretraining, showing the most significant rates of both forgetting and learning. We posit that our research marks a shift towards establishing a more realistic benchmark for investigating CL in LLMs, and has the potential to play a key role in guiding the direction of future research in the field.

Disentangled Continual Learning: Separating Memory Edits from Model Updates

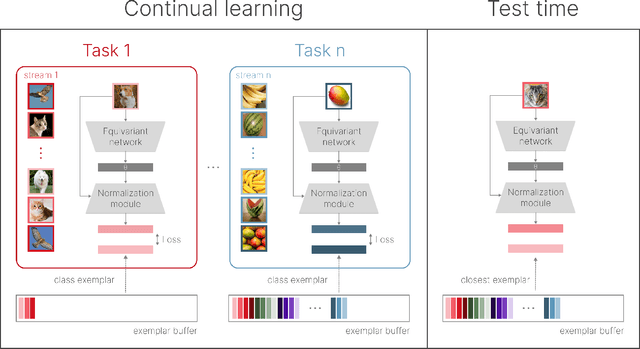
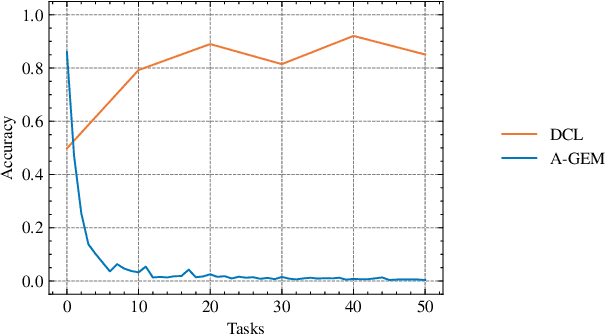
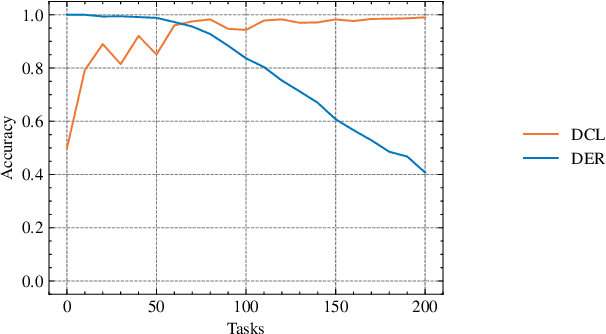
The ability of machine learning systems to learn continually is hindered by catastrophic forgetting, the tendency of neural networks to overwrite existing knowledge when learning a new task. Existing continual learning methods alleviate this problem through regularisation, parameter isolation, or rehearsal, and are typically evaluated on benchmarks consisting of a handful of tasks. We propose a novel conceptual approach to continual classification that aims to disentangle class-specific information that needs to be memorised from the class-agnostic knowledge that encapsulates generalization. We store the former in a buffer that can be easily pruned or updated when new categories arrive, while the latter is represented with a neural network that generalizes across tasks. We show that the class-agnostic network does not suffer from catastrophic forgetting and by leveraging it to perform classification, we improve accuracy on past tasks over time. In addition, our approach supports open-set classification and one-shot generalization. To test our conceptual framework, we introduce Infinite dSprites, a tool for creating continual classification and disentanglement benchmarks of arbitrary length with full control over generative factors. We show that over a sufficiently long time horizon all major types of continual learning methods break down, while our approach enables continual learning over hundreds of tasks with explicit control over memorization and forgetting.

Invariant Neural Ordinary Differential Equations

Latent neural ordinary differential equations have been proven useful for learning non-linear dynamics of arbitrary sequences. In contrast with their mechanistic counterparts, the predictive accuracy of neural ODEs decreases over longer prediction horizons (Rubanova et al., 2019). To mitigate this issue, we propose disentangling dynamic states from time-invariant variables in a completely data-driven way, enabling robust neural ODE models that can generalize across different settings. We show that such variables can control the latent differential function and/or parameterize the mapping from latent variables to observations. By explicitly modeling the time-invariant variables, our framework enables the use of recent advances in representation learning. We demonstrate this by introducing a straightforward self-supervised objective that enhances the learning of these variables. The experiments on low-dimensional oscillating systems and video sequences reveal that our disentangled model achieves improved long-term predictions, when the training data involve sequence-specific factors of variation such as different rotational speeds, calligraphic styles, and friction constants.