Intrinsic Credit Assignment for Long Horizon Interaction

How can we train agents to navigate uncertainty over long horizons? In this work, we propose ΔBelief-RL, which leverages a language model's own intrinsic beliefs to reward intermediate progress. Our method utilizes the change in the probability an agent assigns to the target solution for credit assignment. By training on synthetic interaction data, ΔBelief-RL teaches information-seeking capabilities that consistently outperform purely outcome-based rewards for Reinforcement Learning, with improvements generalizing to out-of-distribution applications ranging from customer service to personalization. Notably, the performance continues to improve as we scale test-time interactions beyond the training horizon, with interaction-efficiency increasing even on Pass@k metrics. Overall, our work introduces a scalable training strategy for navigating uncertainty over a long-horizon, by enabling credit assignment to intermediate actions via intrinsic ΔBelief rewards.

Great Models Think Alike and this Undermines AI Oversight

As Language Model (LM) capabilities advance, evaluating and supervising them at scale is getting harder for humans. There is hope that other language models can automate both these tasks, which we refer to as "AI Oversight". We study how model similarity affects both aspects of AI oversight by proposing a probabilistic metric for LM similarity based on overlap in model mistakes. Using this metric, we first show that LLM-as-a-judge scores favor models similar to the judge, generalizing recent self-preference results. Then, we study training on LM annotations, and find complementary knowledge between the weak supervisor and strong student model plays a crucial role in gains from "weak-to-strong generalization". As model capabilities increase, it becomes harder to find their mistakes, and we might defer more to AI oversight. However, we observe a concerning trend -- model mistakes are becoming more similar with increasing capabilities, pointing to risks from correlated failures. Our work underscores the importance of reporting and correcting for model similarity, especially in the emerging paradigm of AI oversight.

Invariant Neural Ordinary Differential Equations

Latent neural ordinary differential equations have been proven useful for learning non-linear dynamics of arbitrary sequences. In contrast with their mechanistic counterparts, the predictive accuracy of neural ODEs decreases over longer prediction horizons (Rubanova et al., 2019). To mitigate this issue, we propose disentangling dynamic states from time-invariant variables in a completely data-driven way, enabling robust neural ODE models that can generalize across different settings. We show that such variables can control the latent differential function and/or parameterize the mapping from latent variables to observations. By explicitly modeling the time-invariant variables, our framework enables the use of recent advances in representation learning. We demonstrate this by introducing a straightforward self-supervised objective that enhances the learning of these variables. The experiments on low-dimensional oscillating systems and video sequences reveal that our disentangled model achieves improved long-term predictions, when the training data involve sequence-specific factors of variation such as different rotational speeds, calligraphic styles, and friction constants.

ABC-Di: Approximate Bayesian Computation for Discrete Data

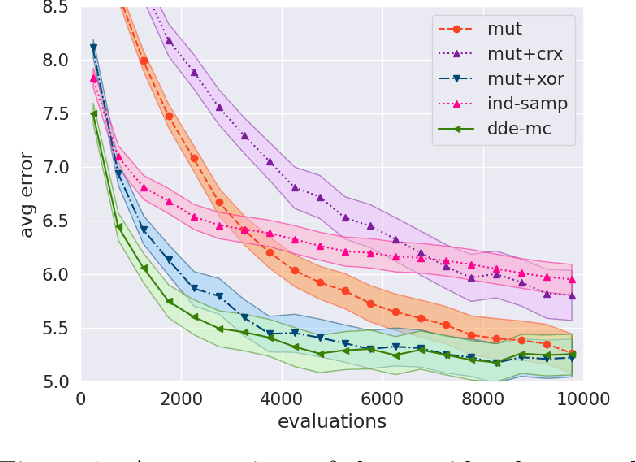
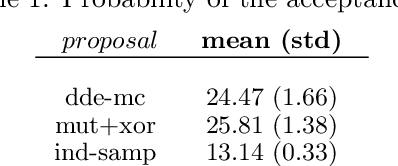
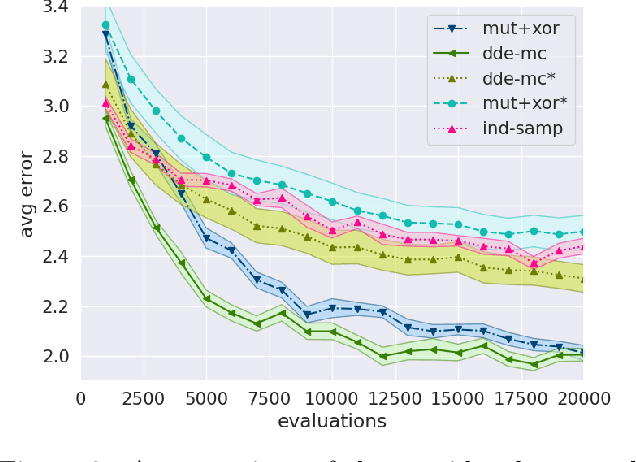
Many real-life problems are represented as a black-box, i.e., the internal workings are inaccessible or a closed-form mathematical expression of the likelihood function cannot be defined. For continuous random variables likelihood-free inference problems can be solved by a group of methods under the name of Approximate Bayesian Computation (ABC). However, a similar approach for discrete random variables is yet to be formulated. Here, we aim to fill this research gap. We propose to use a population-based MCMC ABC framework. Further, we present a valid Markov kernel, and propose a new kernel that is inspired by Differential Evolution. We assess the proposed approach on a problem with the known likelihood function, namely, discovering the underlying diseases based on a QMR-DT Network, and three likelihood-free inference problems: (i) the QMR-DT Network with the unknown likelihood function, (ii) learning binary neural network, and (iii) Neural Architecture Search. The obtained results indicate the high potential of the proposed framework and the superiority of the new Markov kernel.