ABC-Di: Approximate Bayesian Computation for Discrete Data

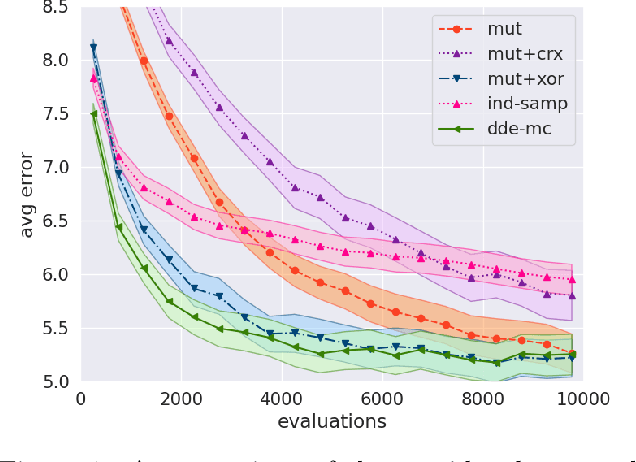
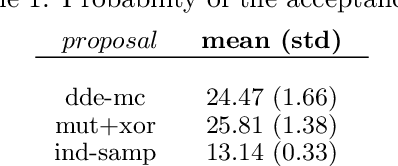
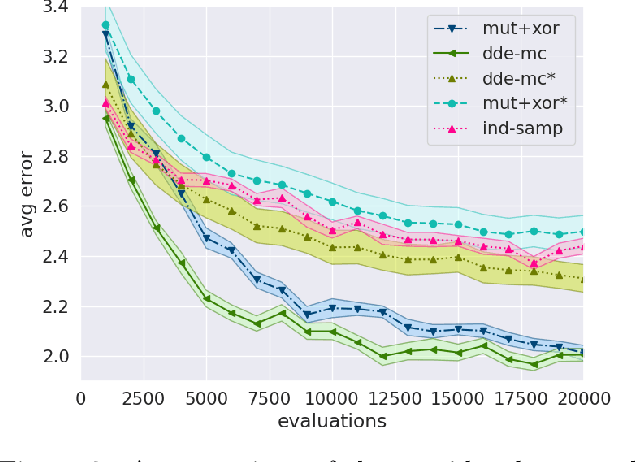
Many real-life problems are represented as a black-box, i.e., the internal workings are inaccessible or a closed-form mathematical expression of the likelihood function cannot be defined. For continuous random variables likelihood-free inference problems can be solved by a group of methods under the name of Approximate Bayesian Computation (ABC). However, a similar approach for discrete random variables is yet to be formulated. Here, we aim to fill this research gap. We propose to use a population-based MCMC ABC framework. Further, we present a valid Markov kernel, and propose a new kernel that is inspired by Differential Evolution. We assess the proposed approach on a problem with the known likelihood function, namely, discovering the underlying diseases based on a QMR-DT Network, and three likelihood-free inference problems: (i) the QMR-DT Network with the unknown likelihood function, (ii) learning binary neural network, and (iii) Neural Architecture Search. The obtained results indicate the high potential of the proposed framework and the superiority of the new Markov kernel.