Wasserstein Variational Inference

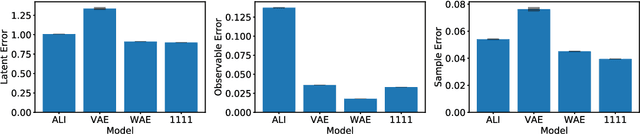
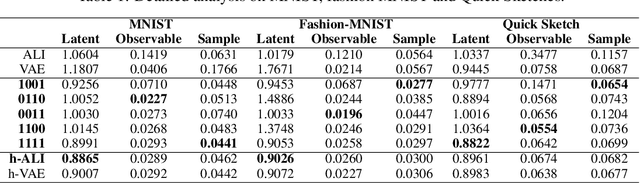
This paper introduces Wasserstein variational inference, a new form of approximate Bayesian inference based on optimal transport theory. Wasserstein variational inference uses a new family of divergences that includes both f-divergences and the Wasserstein distance as special cases. The gradients of the Wasserstein variational loss are obtained by backpropagating through the Sinkhorn iterations. This technique results in a very stable likelihood-free training method that can be used with implicit distributions and probabilistic programs. Using the Wasserstein variational inference framework, we introduce several new forms of autoencoders and test their robustness and performance against existing variational autoencoding techniques.

Forward Amortized Inference for Likelihood-Free Variational Marginalization

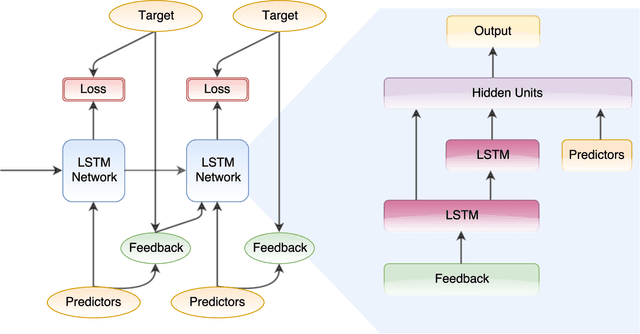
In this paper, we introduce a new form of amortized variational inference by using the forward KL divergence in a joint-contrastive variational loss. The resulting forward amortized variational inference is a likelihood-free method as its gradient can be sampled without bias and without requiring any evaluation of either the model joint distribution or its derivatives. We prove that our new variational loss is optimized by the exact posterior marginals in the fully factorized mean-field approximation, a property that is not shared with the more conventional reverse KL inference. Furthermore, we show that forward amortized inference can be easily marginalized over large families of latent variables in order to obtain a marginalized variational posterior. We consider two examples of variational marginalization. In our first example we train a Bayesian forecaster for predicting a simplified chaotic model of atmospheric convection. In the second example we train an amortized variational approximation of a Bayesian optimal classifier by marginalizing over the model space. The result is a powerful meta-classification network that can solve arbitrary classification problems without further training.

Complex-valued Gaussian Process Regression for Time Series Analysis

The construction of synthetic complex-valued signals from real-valued observations is an important step in many time series analysis techniques. The most widely used approach is based on the Hilbert transform, which maps the real-valued signal into its quadrature component. In this paper, we define a probabilistic generalization of this approach. We model the observable real-valued signal as the real part of a latent complex-valued Gaussian process. In order to obtain the appropriate statistical relationship between its real and imaginary parts, we define two new classes of complex-valued covariance functions. Through an analysis of simulated chirplets and stochastic oscillations, we show that the resulting Gaussian process complex-valued signal provides a better estimate of the instantaneous amplitude and frequency than the established approaches. Furthermore, the complex-valued Gaussian process regression allows to incorporate prior information about the structure in signal and noise and thereby to tailor the analysis to the features of the signal. As a example, we analyze the non-stationary dynamics of brain oscillations in the alpha band, as measured using magneto-encephalography.

Integral Transforms from Finite Data: An Application of Gaussian Process Regression to Fourier Analysis

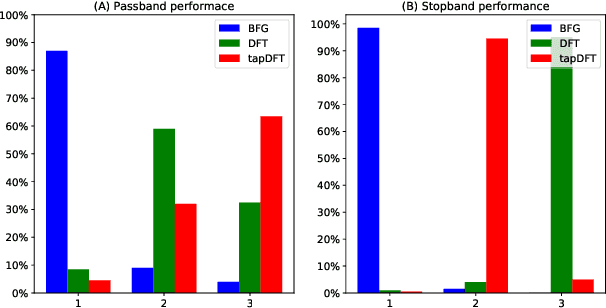
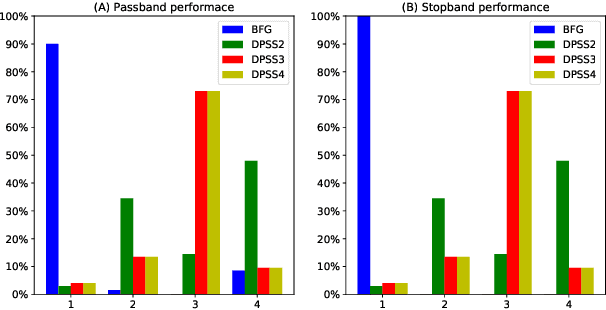
Computing accurate estimates of the Fourier transform of analog signals from discrete data points is important in many fields of science and engineering. The conventional approach of performing the discrete Fourier transform of the data implicitly assumes periodicity and bandlimitedness of the signal. In this paper, we use Gaussian process regression to estimate the Fourier transform (or any other integral transform) without making these assumptions. This is possible because the posterior expectation of Gaussian process regression maps a finite set of samples to a function defined on the whole real line, expressed as a linear combination of covariance functions. We estimate the covariance function from the data using an appropriately designed gradient ascent method that constrains the solution to a linear combination of tractable kernel functions. This procedure results in a posterior expectation of the analog signal whose Fourier transform can be obtained analytically by exploiting linearity. Our simulations show that the new method leads to sharper and more precise estimation of the spectral density both in noise-free and noise-corrupted signals. We further validate the method in two real-world applications: the analysis of the yearly fluctuation in atmospheric CO2 level and the analysis of the spectral content of brain signals.

The Kernel Mixture Network: A Nonparametric Method for Conditional Density Estimation of Continuous Random Variables

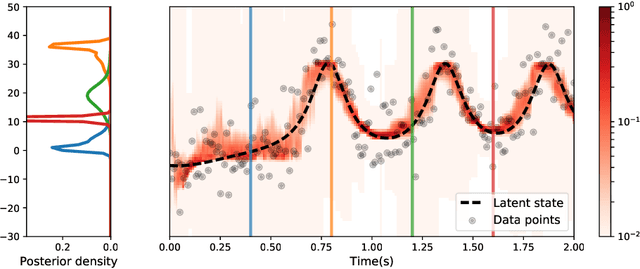
This paper introduces the kernel mixture network, a new method for nonparametric estimation of conditional probability densities using neural networks. We model arbitrarily complex conditional densities as linear combinations of a family of kernel functions centered at a subset of training points. The weights are determined by the outer layer of a deep neural network, trained by minimizing the negative log likelihood. This generalizes the popular quantized softmax approach, which can be seen as a kernel mixture network with square and non-overlapping kernels. We test the performance of our method on two important applications, namely Bayesian filtering and generative modeling. In the Bayesian filtering example, we show that the method can be used to filter complex nonlinear and non-Gaussian signals defined on manifolds. The resulting kernel mixture network filter outperforms both the quantized softmax filter and the extended Kalman filter in terms of model likelihood. Finally, our experiments on generative models show that, given the same architecture, the kernel mixture network leads to higher test set likelihood, less overfitting and more diversified and realistic generated samples than the quantized softmax approach.

GP CaKe: Effective brain connectivity with causal kernels

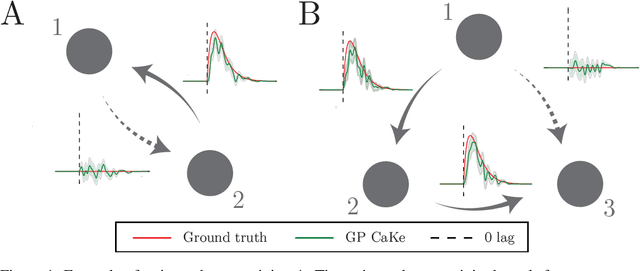
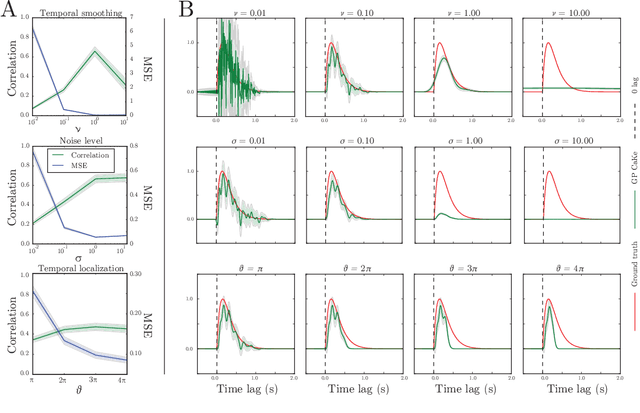
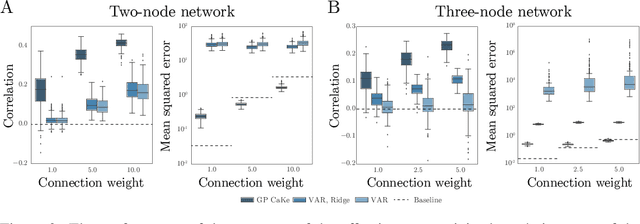
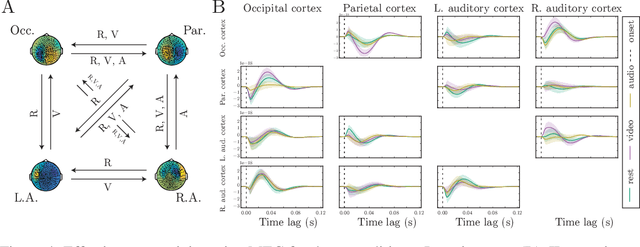
A fundamental goal in network neuroscience is to understand how activity in one region drives activity elsewhere, a process referred to as effective connectivity. Here we propose to model this causal interaction using integro-differential equations and causal kernels that allow for a rich analysis of effective connectivity. The approach combines the tractability and flexibility of autoregressive modeling with the biophysical interpretability of dynamic causal modeling. The causal kernels are learned nonparametrically using Gaussian process regression, yielding an efficient framework for causal inference. We construct a novel class of causal covariance functions that enforce the desired properties of the causal kernels, an approach which we call GP CaKe. By construction, the model and its hyperparameters have biophysical meaning and are therefore easily interpretable. We demonstrate the efficacy of GP CaKe on a number of simulations and give an example of a realistic application on magnetoencephalography (MEG) data.

Estimating Nonlinear Dynamics with the ConvNet Smoother

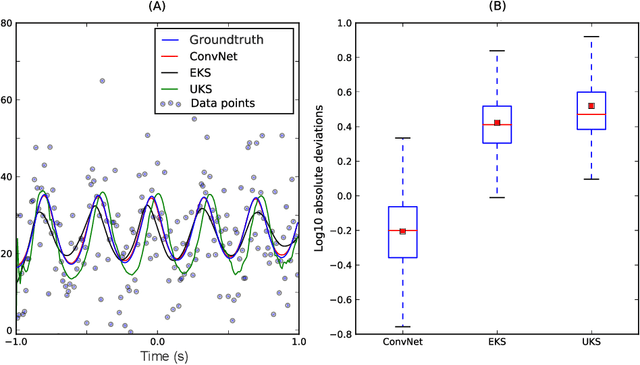
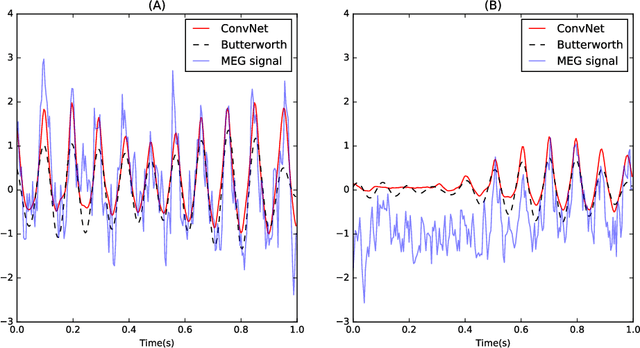
Estimating the state of a dynamical system from a series of noise-corrupted observations is fundamental in many areas of science and engineering. The most well-known method, the Kalman smoother (and the related Kalman filter), relies on assumptions of linearity and Gaussianity that are rarely met in practice. In this paper, we introduced a new dynamical smoothing method that exploits the remarkable capabilities of convolutional neural networks to approximate complex non-linear functions. The main idea is to generate a training set composed of both latent states and observations from an ensemble of simulators and to train the deep network to recover the former from the latter. Importantly, this method only requires the availability of the simulators and can therefore be applied in situations in which either the latent dynamical model or the observation model cannot be easily expressed in closed form. In our simulation studies, we show that the resulting ConvNet smoother has almost optimal performance in the Gaussian case even when the parameters are unknown. Furthermore, the method can be successfully applied to extremely non-linear and non-Gaussian systems. Finally, we empirically validate our approach via the analysis of measured brain signals.

Analysis of Nonstationary Time Series Using Locally Coupled Gaussian Processes

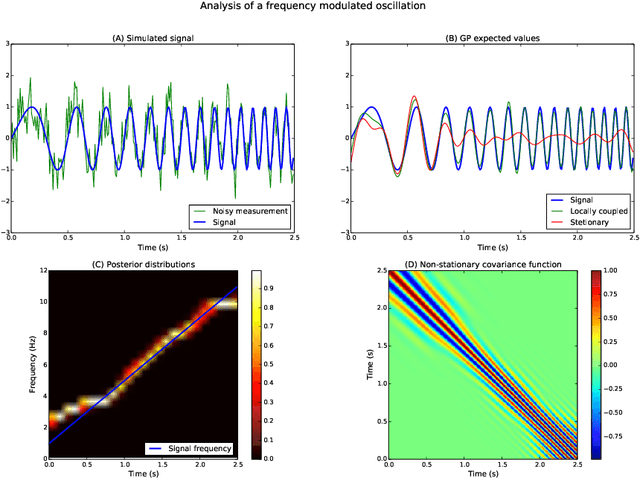
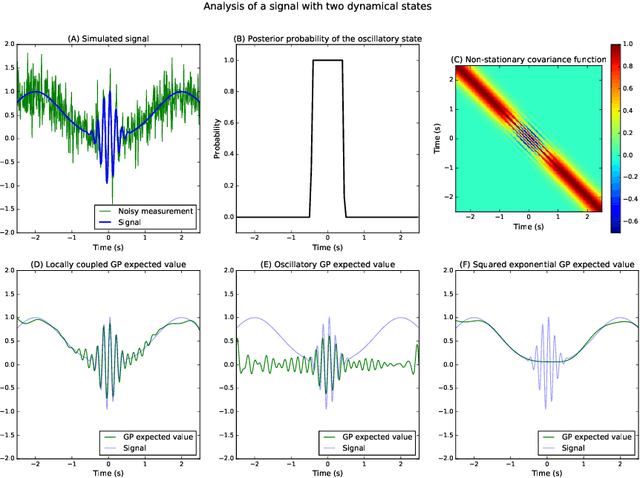
The analysis of nonstationary time series is of great importance in many scientific fields such as physics and neuroscience. In recent years, Gaussian process regression has attracted substantial attention as a robust and powerful method for analyzing time series. In this paper, we introduce a new framework for analyzing nonstationary time series using locally stationary Gaussian process analysis with parameters that are coupled through a hidden Markov model. The main advantage of this framework is that arbitrary complex nonstationary covariance functions can be obtained by combining simpler stationary building blocks whose hidden parameters can be estimated in closed-form. We demonstrate the flexibility of the method by analyzing two examples of synthetic nonstationary signals: oscillations with time varying frequency and time series with two dynamical states. Finally, we report an example application on real magnetoencephalographic measurements of brain activity.

Dynamic Decomposition of Spatiotemporal Neural Signals

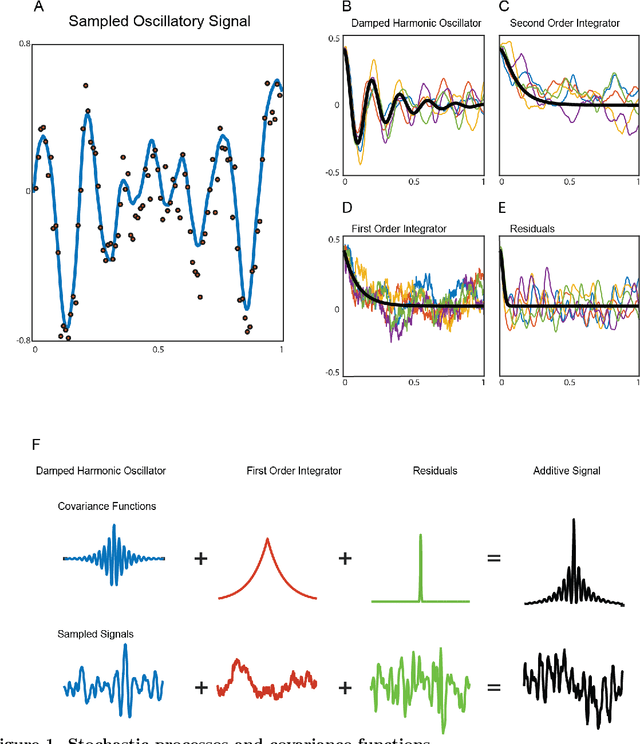
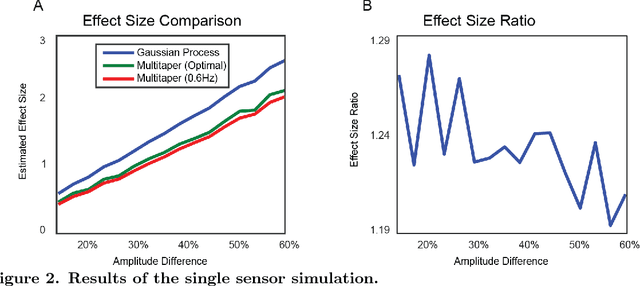
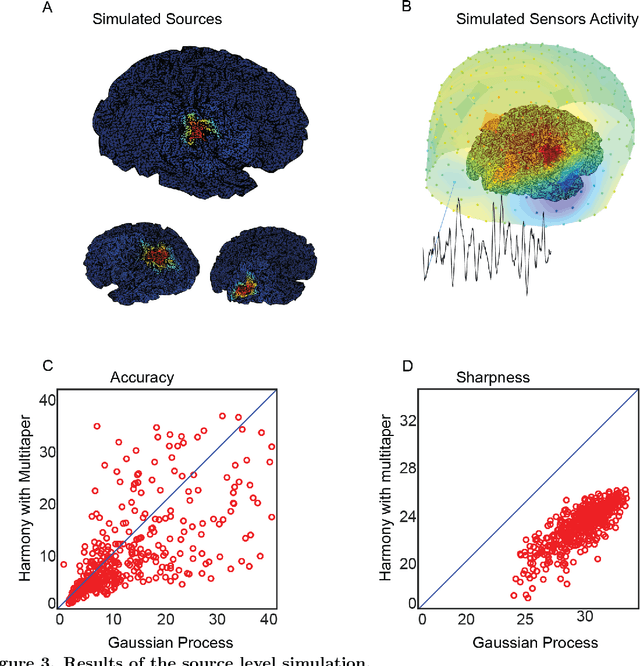
Neural signals are characterized by rich temporal and spatiotemporal dynamics that reflect the organization of cortical networks. Theoretical research has shown how neural networks can operate at different dynamic ranges that correspond to specific types of information processing. Here we present a data analysis framework that uses a linearized model of these dynamic states in order to decompose the measured neural signal into a series of components that capture both rhythmic and non-rhythmic neural activity. The method is based on stochastic differential equations and Gaussian process regression. Through computer simulations and analysis of magnetoencephalographic data, we demonstrate the efficacy of the method in identifying meaningful modulations of oscillatory signals corrupted by structured temporal and spatiotemporal noise. These results suggest that the method is particularly suitable for the analysis and interpretation of complex temporal and spatiotemporal neural signals.