Measuring Semantic Information Production in Generative Diffusion Models

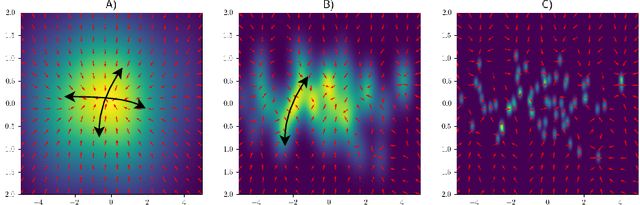
It is well known that semantic and structural features of the generated images emerge at different times during the reverse dynamics of diffusion, a phenomenon that has been connected to physical phase transitions in magnets and other materials. In this paper, we introduce a general information-theoretic approach to measure when these class-semantic "decisions" are made during the generative process. By using an online formula for the optimal Bayesian classifier, we estimate the conditional entropy of the class label given the noisy state. We then determine the time intervals corresponding to the highest information transfer between noisy states and class labels using the time derivative of the conditional entropy. We demonstrate our method on one-dimensional Gaussian mixture models and on DDPM models trained on the CIFAR10 dataset. As expected, we find that the semantic information transfer is highest in the intermediate stages of diffusion while vanishing during the final stages. However, we found sizable differences between the entropy rate profiles of different classes, suggesting that different "semantic decisions" are located at different intermediate times.

Memorization to Generalization: Emergence of Diffusion Models from Associative Memory

Hopfield networks are associative memory (AM) systems, designed for storing and retrieving patterns as local minima of an energy landscape. In the classical Hopfield model, an interesting phenomenon occurs when the amount of training data reaches its critical memory load $- spurious\,\,states$, or unintended stable points, emerge at the end of the retrieval dynamics, leading to incorrect recall. In this work, we examine diffusion models, commonly used in generative modeling, from the perspective of AMs. The training phase of diffusion model is conceptualized as memory encoding (training data is stored in the memory). The generation phase is viewed as an attempt of memory retrieval. In the small data regime the diffusion model exhibits a strong memorization phase, where the network creates distinct basins of attraction around each sample in the training set, akin to the Hopfield model below the critical memory load. In the large data regime, a different phase appears where an increase in the size of the training set fosters the creation of new attractor states that correspond to manifolds of the generated samples. Spurious states appear at the boundary of this transition and correspond to emergent attractor states, which are absent in the training set, but, at the same time, have distinct basins of attraction around them. Our findings provide: a novel perspective on the memorization-generalization phenomenon in diffusion models via the lens of AMs, theoretical prediction of existence of spurious states, empirical validation of this prediction in commonly-used diffusion models.

Entropic Time Schedulers for Generative Diffusion Models

The practical performance of generative diffusion models depends on the appropriate choice of the noise scheduling function, which can also be equivalently expressed as a time reparameterization. In this paper, we present a time scheduler that selects sampling points based on entropy rather than uniform time spacing, ensuring that each point contributes an equal amount of information to the final generation. We prove that this time reparameterization does not depend on the initial choice of time. Furthermore, we provide a tractable exact formula to estimate this \emph{entropic time} for a trained model using the training loss without substantial overhead. Alongside the entropic time, inspired by the optimality results, we introduce a rescaled entropic time. In our experiments with mixtures of Gaussian distributions and ImageNet, we show that using the (rescaled) entropic times greatly improves the inference performance of trained models. In particular, we found that the image quality in pretrained EDM2 models, as evaluated by FID and FD-DINO scores, can be substantially increased by the rescaled entropic time reparameterization without increasing the number of function evaluations, with greater improvements in the few NFEs regime.

Training Consistency Models with Variational Noise Coupling

Consistency Training (CT) has recently emerged as a promising alternative to diffusion models, achieving competitive performance in image generation tasks. However, non-distillation consistency training often suffers from high variance and instability, and analyzing and improving its training dynamics is an active area of research. In this work, we propose a novel CT training approach based on the Flow Matching framework. Our main contribution is a trained noise-coupling scheme inspired by the architecture of Variational Autoencoders (VAE). By training a data-dependent noise emission model implemented as an encoder architecture, our method can indirectly learn the geometry of the noise-to-data mapping, which is instead fixed by the choice of the forward process in classical CT. Empirical results across diverse image datasets show significant generative improvements, with our model outperforming baselines and achieving the state-of-the-art (SoTA) non-distillation CT FID on CIFAR-10, and attaining FID on par with SoTA on ImageNet at $64 \times 64$ resolution in 2-step generation. Our code is available at https://github.com/sony/vct .

Dynamic Negative Guidance of Diffusion Models

Negative Prompting (NP) is widely utilized in diffusion models, particularly in text-to-image applications, to prevent the generation of undesired features. In this paper, we show that conventional NP is limited by the assumption of a constant guidance scale, which may lead to highly suboptimal results, or even complete failure, due to the non-stationarity and state-dependence of the reverse process. Based on this analysis, we derive a principled technique called Dynamic Negative Guidance, which relies on a near-optimal time and state dependent modulation of the guidance without requiring additional training. Unlike NP, negative guidance requires estimating the posterior class probability during the denoising process, which is achieved with limited additional computational overhead by tracking the discrete Markov Chain during the generative process. We evaluate the performance of DNG class-removal on MNIST and CIFAR10, where we show that DNG leads to higher safety, preservation of class balance and image quality when compared with baseline methods. Furthermore, we show that it is possible to use DNG with Stable Diffusion to obtain more accurate and less invasive guidance than NP.

Losing dimensions: Geometric memorization in generative diffusion

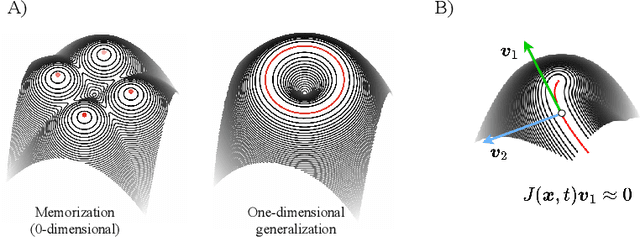
Generative diffusion processes are state-of-the-art machine learning models deeply connected with fundamental concepts in statistical physics. Depending on the dataset size and the capacity of the network, their behavior is known to transition from an associative memory regime to a generalization phase in a phenomenon that has been described as a glassy phase transition. Here, using statistical physics techniques, we extend the theory of memorization in generative diffusion to manifold-supported data. Our theoretical and experimental findings indicate that different tangent subspaces are lost due to memorization effects at different critical times and dataset sizes, which depend on the local variance of the data along their directions. Perhaps counterintuitively, we find that, under some conditions, subspaces of higher variance are lost first due to memorization effects. This leads to a selective loss of dimensionality where some prominent features of the data are memorized without a full collapse on any individual training point. We validate our theory with a comprehensive set of experiments on networks trained both in image datasets and on linear manifolds, which result in a remarkable qualitative agreement with the theoretical predictions.

Manifolds, Random Matrices and Spectral Gaps: The geometric phases of generative diffusion

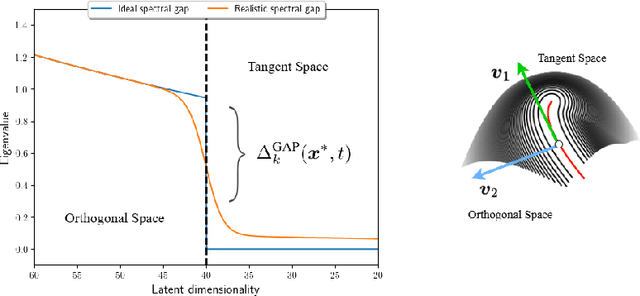
In this paper, we investigate the latent geometry of generative diffusion models under the manifold hypothesis. To this purpose, we analyze the spectrum of eigenvalues (and singular values) of the Jacobian of the score function, whose discontinuities (gaps) reveal the presence and dimensionality of distinct sub-manifolds. Using a statistical physics approach, we derive the spectral distributions and formulas for the spectral gaps under several distributional assumptions and we compare these theoretical predictions with the spectra estimated from trained networks. Our analysis reveals the existence of three distinct qualitative phases during the generative process: a trivial phase; a manifold coverage phase where the diffusion process fits the distribution internal to the manifold; a consolidation phase where the score becomes orthogonal to the manifold and all particles are projected on the support of the data. This `division of labor' between different timescales provides an elegant explanation on why generative diffusion models are not affected by the manifold overfitting phenomenon that plagues likelihood-based models, since the internal distribution and the manifold geometry are produced at different time points during generation.

Robust and highly scalable estimation of directional couplings from time-shifted signals

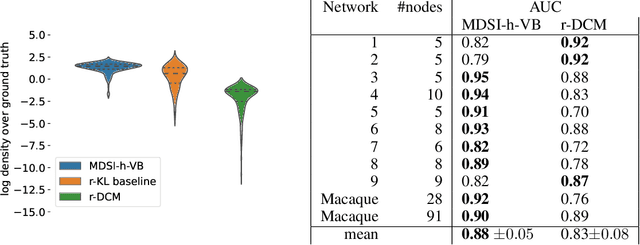
The estimation of directed couplings between the nodes of a network from indirect measurements is a central methodological challenge in scientific fields such as neuroscience, systems biology and economics. Unfortunately, the problem is generally ill-posed due to the possible presence of unknown delays in the measurements. In this paper, we offer a solution of this problem by using a variational Bayes framework, where the uncertainty over the delays is marginalized in order to obtain conservative coupling estimates. To overcome the well-known overconfidence of classical variational methods, we use a hybrid-VI scheme where the (possibly flat or multimodal) posterior over the measurement parameters is estimated using a forward KL loss while the (nearly convex) conditional posterior over the couplings is estimated using the highly scalable gradient-based VI. In our ground-truth experiments, we show that the network provides reliable and conservative estimates of the couplings, greatly outperforming similar methods such as regression DCM.

The statistical thermodynamics of generative diffusion models

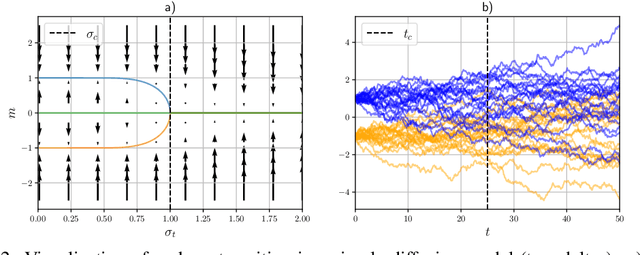
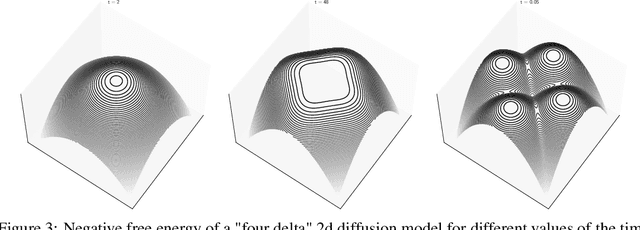
Generative diffusion models have achieved spectacular performance in many areas of generative modeling. While the fundamental ideas behind these models come from non-equilibrium physics, in this paper we show that many aspects of these models can be understood using the tools of equilibrium statistical mechanics. Using this reformulation, we show that generative diffusion models undergo second-order phase transitions corresponding to symmetry breaking phenomena. We argue that this lead to a form of instability that lies at the heart of their generative capabilities and that can be described by a set of mean field critical exponents. We conclude by analyzing recent work connecting diffusion models and associative memory networks in view of the thermodynamic formulations.

Stationarity without mean reversion: Improper Gaussian process regression and improper kernels

Gaussian processes (GP) regression has gained substantial popularity in machine learning applications. The behavior of a GP regression depends on the choice of covariance function. Stationary covariance functions are favorite in machine learning applications. However, (non-periodic) stationary covariance functions are always mean reverting and can therefore exhibit pathological behavior when applied to data that does not relax to a fixed global mean value. In this paper, we show that it is possible to use improper GP prior with infinite variance to define processes that are stationary but not mean reverting. To this aim, we introduce a large class of improper kernels that can only be defined in this improper regime. Specifically, we introduce the Smooth Walk kernel, which produces infinitely smooth samples, and a family of improper Mat\'ern kernels, which can be defined to be $j$-times differentiable for any integer $j$. The resulting posterior distributions can be computed analytically and it involves a simple correction of the usual formulas. By analyzing both synthetic and real data, we demonstrate that these improper kernels solve some known pathologies of mean reverting GP regression while retaining most of the favourable properties of ordinary smooth stationary kernels.