Robust and highly scalable estimation of directional couplings from time-shifted signals

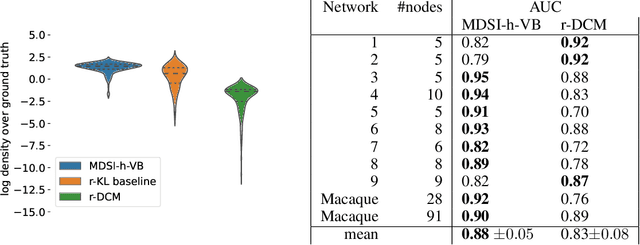
The estimation of directed couplings between the nodes of a network from indirect measurements is a central methodological challenge in scientific fields such as neuroscience, systems biology and economics. Unfortunately, the problem is generally ill-posed due to the possible presence of unknown delays in the measurements. In this paper, we offer a solution of this problem by using a variational Bayes framework, where the uncertainty over the delays is marginalized in order to obtain conservative coupling estimates. To overcome the well-known overconfidence of classical variational methods, we use a hybrid-VI scheme where the (possibly flat or multimodal) posterior over the measurement parameters is estimated using a forward KL loss while the (nearly convex) conditional posterior over the couplings is estimated using the highly scalable gradient-based VI. In our ground-truth experiments, we show that the network provides reliable and conservative estimates of the couplings, greatly outperforming similar methods such as regression DCM.

PAVI: Plate-Amortized Variational Inference

Given observed data and a probabilistic generative model, Bayesian inference searches for the distribution of the model's parameters that could have yielded the data. Inference is challenging for large population studies where millions of measurements are performed over a cohort of hundreds of subjects, resulting in a massive parameter space. This large cardinality renders off-the-shelf Variational Inference (VI) computationally impractical. In this work, we design structured VI families that efficiently tackle large population studies. Our main idea is to share the parameterization and learning across the different i.i.d. variables in a generative model, symbolized by the model's \textit{plates}. We name this concept \textit{plate amortization}. Contrary to off-the-shelf stochastic VI, which slows down inference, plate amortization results in orders of magnitude faster to train variational distributions. Applied to large-scale hierarchical problems, PAVI yields expressive, parsimoniously parameterized VI with an affordable training time. This faster convergence effectively unlocks inference in those large regimes. We illustrate the practical utility of PAVI through a challenging Neuroimaging example featuring 400 million latent parameters, demonstrating a significant step towards scalable and expressive Variational Inference.

ADAVI: Automatic Dual Amortized Variational Inference Applied To Pyramidal Bayesian Models

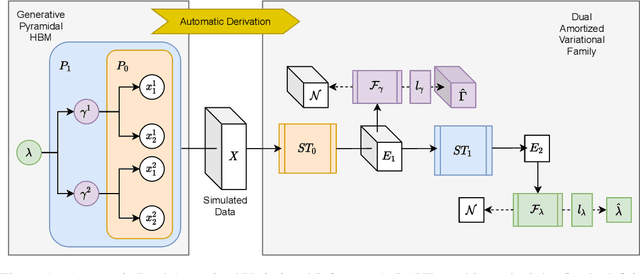
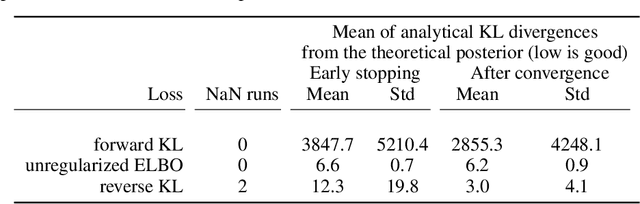
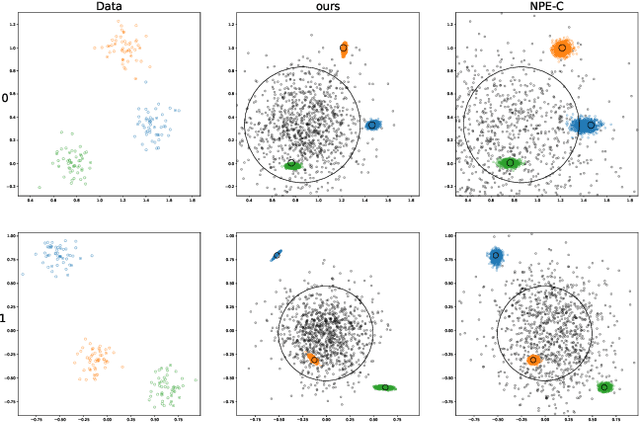
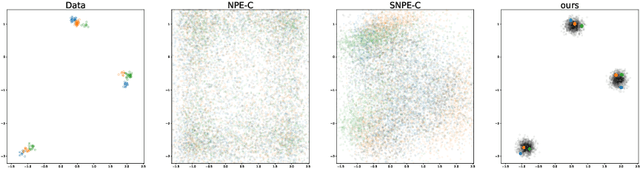
Frequently, population studies feature pyramidally-organized data represented using Hierarchical Bayesian Models (HBM) enriched with plates. These models can become prohibitively large in settings such as neuroimaging, where a sample is composed of a functional MRI signal measured on 64 thousand brain locations, across 4 measurement sessions, and at least tens of subjects. Even a reduced example on a specific cortical region of 300 brain locations features around 1 million parameters, hampering the usage of modern density estimation techniques such as Simulation-Based Inference (SBI). To infer parameter posterior distributions in this challenging class of problems, we designed a novel methodology that automatically produces a variational family dual to a target HBM. This variatonal family, represented as a neural network, consists in the combination of an attention-based hierarchical encoder feeding summary statistics to a set of normalizing flows. Our automatically-derived neural network exploits exchangeability in the plate-enriched HBM and factorizes its parameter space. The resulting architecture reduces by orders of magnitude its parameterization with respect to that of a typical SBI representation, while maintaining expressivity. Our method performs inference on the specified HBM in an amortized setup: once trained, it can readily be applied to a new data sample to compute the parameters' full posterior. We demonstrate the capability of our method on simulated data, as well as a challenging high-dimensional brain parcellation experiment. We also open up several questions that lie at the intersection between SBI techniques and structured Variational Inference.