Analysis of Nonstationary Time Series Using Locally Coupled Gaussian Processes
Paper and Code
Oct 31, 2016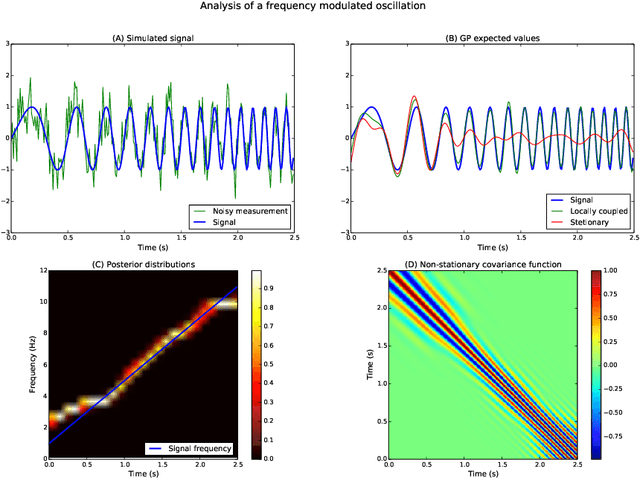
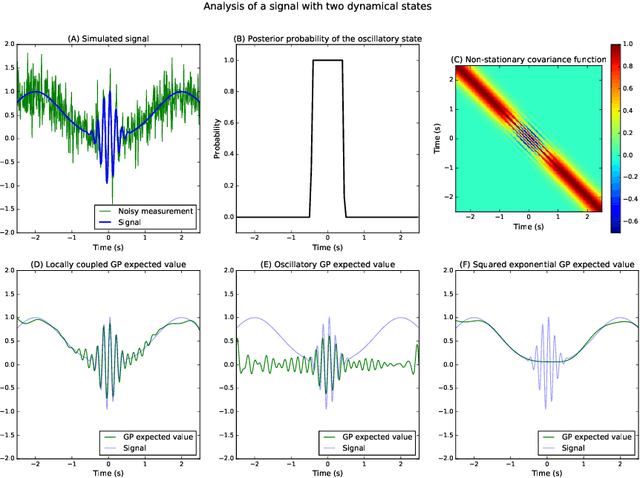

The analysis of nonstationary time series is of great importance in many scientific fields such as physics and neuroscience. In recent years, Gaussian process regression has attracted substantial attention as a robust and powerful method for analyzing time series. In this paper, we introduce a new framework for analyzing nonstationary time series using locally stationary Gaussian process analysis with parameters that are coupled through a hidden Markov model. The main advantage of this framework is that arbitrary complex nonstationary covariance functions can be obtained by combining simpler stationary building blocks whose hidden parameters can be estimated in closed-form. We demonstrate the flexibility of the method by analyzing two examples of synthetic nonstationary signals: oscillations with time varying frequency and time series with two dynamical states. Finally, we report an example application on real magnetoencephalographic measurements of brain activity.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge