The Indian Chefs Process

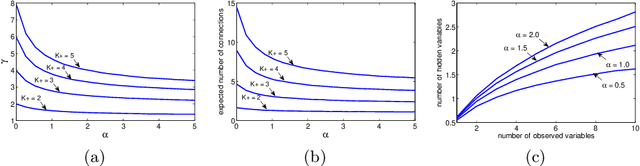
This paper introduces the Indian Chefs Process (ICP), a Bayesian nonparametric prior on the joint space of infinite directed acyclic graphs (DAGs) and orders that generalizes Indian Buffet Processes. As our construction shows, the proposed distribution relies on a latent Beta Process controlling both the orders and outgoing connection probabilities of the nodes, and yields a probability distribution on sparse infinite graphs. The main advantage of the ICP over previously proposed Bayesian nonparametric priors for DAG structures is its greater flexibility. To the best of our knowledge, the ICP is the first Bayesian nonparametric model supporting every possible DAG. We demonstrate the usefulness of the ICP on learning the structure of deep generative sigmoid networks as well as convolutional neural networks.

Adaptive Deep Kernel Learning

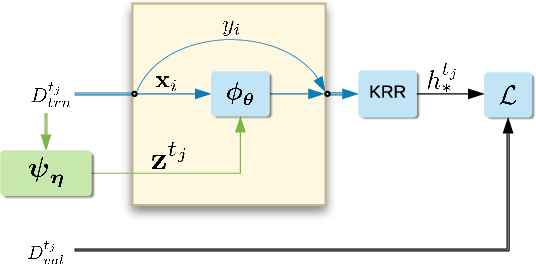
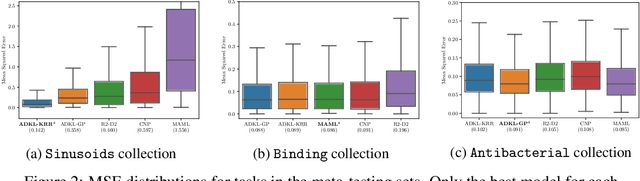
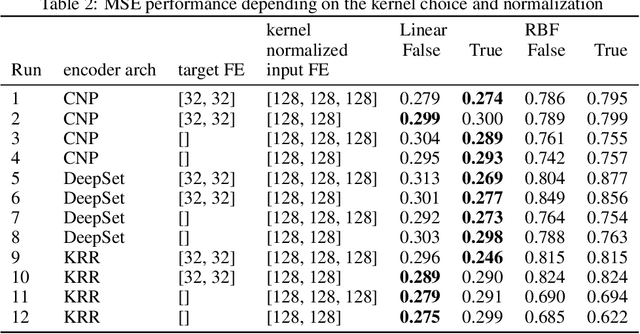
Deep kernel learning provides an elegant and principled framework for combining the structural properties of deep learning algorithms with the flexibility of kernel methods. By means of a deep neural network, it consists of learning a kernel operator which is combined with a differentiable kernel algorithm for inference. While previous work within this framework has mostly explored learning a single kernel for large datasets, we focus herein on learning a kernel family for a variety of tasks in few-shot regression settings. Compared to single deep kernel learning, our novel algorithm permits finding the appropriate kernel for each task during inference, rather than using the same for all tasks. As such, our algorithm performs more effectively with complex task distributions in few-shot learning, which we demonstrate by benchmarking against existing state-of-the-art algorithms using real-world, few-shot regression tasks related to drug discovery.

An Improvement to the Domain Adaptation Bound in a PAC-Bayesian context

This paper provides a theoretical analysis of domain adaptation based on the PAC-Bayesian theory. We propose an improvement of the previous domain adaptation bound obtained by Germain et al. in two ways. We first give another generalization bound tighter and easier to interpret. Moreover, we provide a new analysis of the constant term appearing in the bound that can be of high interest for developing new algorithmic solutions.

On Generalizing the C-Bound to the Multiclass and Multi-label Settings

The C-bound, introduced in Lacasse et al., gives a tight upper bound on the risk of a binary majority vote classifier. In this work, we present a first step towards extending this work to more complex outputs, by providing generalizations of the C-bound to the multiclass and multi-label settings.