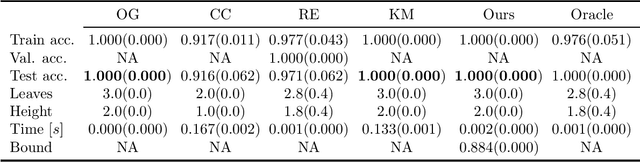
Mixtures of Transparent Local Models

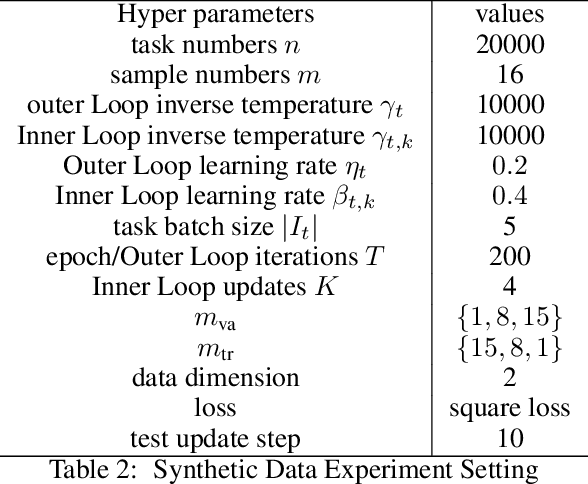
The predominance of machine learning models in many spheres of human activity has led to a growing demand for their transparency. The transparency of models makes it possible to discern some factors, such as security or non-discrimination. In this paper, we propose a mixture of transparent local models as an alternative solution for designing interpretable (or transparent) models. Our approach is designed for the situations where a simple and transparent function is suitable for modeling the label of instances in some localities/regions of the input space, but may change abruptly as we move from one locality to another. Consequently, the proposed algorithm is to learn both the transparent labeling function and the locality of the input space where the labeling function achieves a small risk in its assigned locality. By using a new multi-predictor (and multi-locality) loss function, we established rigorous PAC-Bayesian risk bounds for the case of binary linear classification problem and that of linear regression. In both cases, synthetic data sets were used to illustrate how the learning algorithms work. The results obtained from real data sets highlight the competitiveness of our approach compared to other existing methods as well as certain opaque models. Keywords: PAC-Bayes, risk bounds, local models, transparent models, mixtures of local transparent models.

Tighter Risk Bounds for Mixtures of Experts

In this work, we provide upper bounds on the risk of mixtures of experts by imposing local differential privacy (LDP) on their gating mechanism. These theoretical guarantees are tailored to mixtures of experts that utilize the one-out-of-$n$ gating mechanism, as opposed to the conventional $n$-out-of-$n$ mechanism. The bounds exhibit logarithmic dependence on the number of experts, and encapsulate the dependence on the gating mechanism in the LDP parameter, making them significantly tighter than existing bounds, under reasonable conditions. Experimental results support our theory, demonstrating that our approach enhances the generalization ability of mixtures of experts and validating the feasibility of imposing LDP on the gating mechanism.

Algorithm-Dependent Bounds for Representation Learning of Multi-Source Domain Adaptation

We use information-theoretic tools to derive a novel analysis of Multi-source Domain Adaptation (MDA) from the representation learning perspective. Concretely, we study joint distribution alignment for supervised MDA with few target labels and unsupervised MDA with pseudo labels, where the latter is relatively hard and less commonly studied. We further provide algorithm-dependent generalization bounds for these two settings, where the generalization is characterized by the mutual information between the parameters and the data. Then we propose a novel deep MDA algorithm, implicitly addressing the target shift through joint alignment. Finally, the mutual information bounds are extended to this algorithm providing a non-vacuous gradient-norm estimation. The proposed algorithm has comparable performance to the state-of-the-art on target-shifted MDA benchmark with improved memory efficiency.

Generalization Properties of Decision Trees on Real-valued and Categorical Features

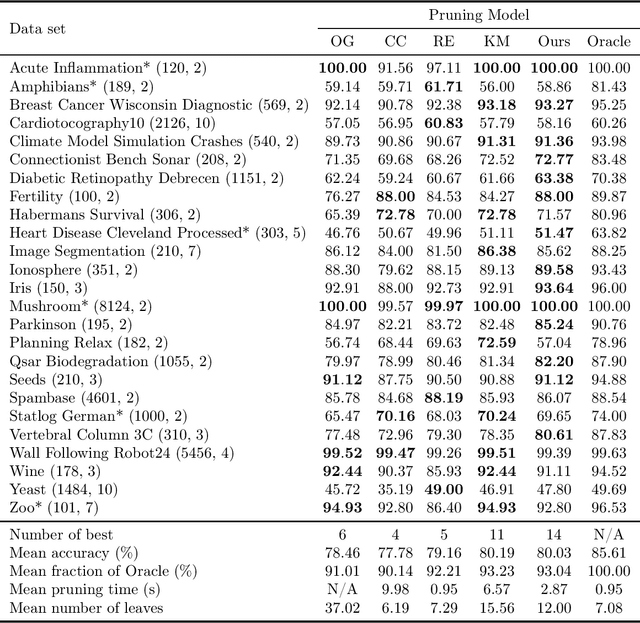
We revisit binary decision trees from the perspective of partitions of the data. We introduce the notion of partitioning function, and we relate it to the growth function and to the VC dimension. We consider three types of features: real-valued, categorical ordinal and categorical nominal, with different split rules for each. For each feature type, we upper bound the partitioning function of the class of decision stumps before extending the bounds to the class of general decision tree (of any fixed structure) using a recursive approach. Using these new results, we are able to find the exact VC dimension of decision stumps on examples of $\ell$ real-valued features, which is given by the largest integer $d$ such that $2\ell \ge \binom{d}{\lfloor\frac{d}{2}\rfloor}$. Furthermore, we show that the VC dimension of a binary tree structure with $L_T$ leaves on examples of $\ell$ real-valued features is in $O(L_T \log(L_T\ell))$. Finally, we elaborate a pruning algorithm based on these results that performs better than the cost-complexity and reduced-error pruning algorithms on a number of data sets, with the advantage that no cross-validation is required.

Improving Generalization Bounds for VC Classes Using the Hypergeometric Tail Inversion

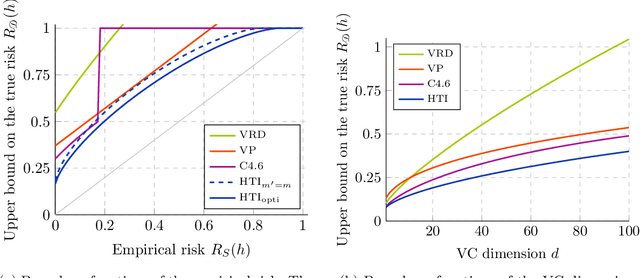
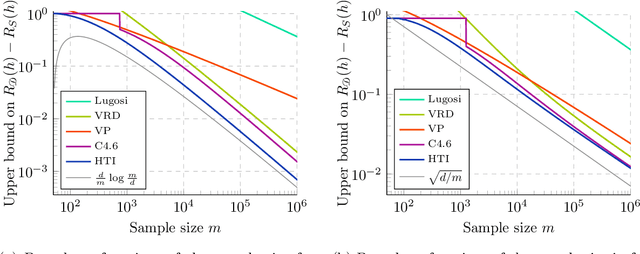
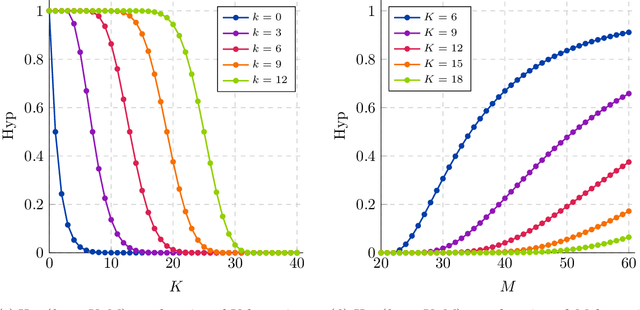
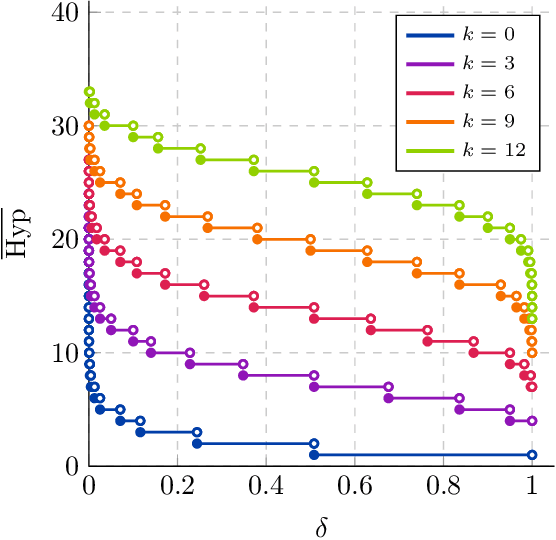
We significantly improve the generalization bounds for VC classes by using two main ideas. First, we consider the hypergeometric tail inversion to obtain a very tight non-uniform distribution-independent risk upper bound for VC classes. Second, we optimize the ghost sample trick to obtain a further non-negligible gain. These improvements are then used to derive a relative deviation bound, a multiclass margin bound, as well as a lower bound. Numerical comparisons show that the new bound is nearly never vacuous, and is tighter than other VC bounds for all reasonable data set sizes.

Partial order: Finding Consensus among Uncertain Feature Attributions

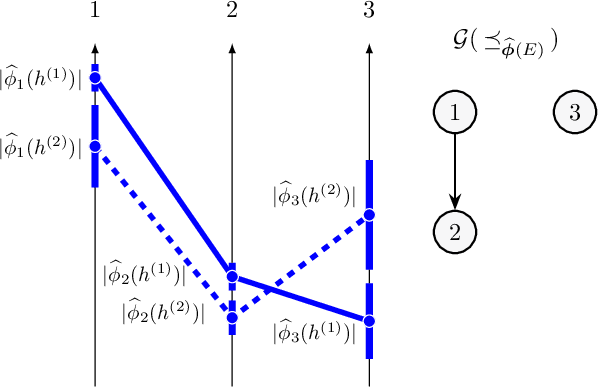
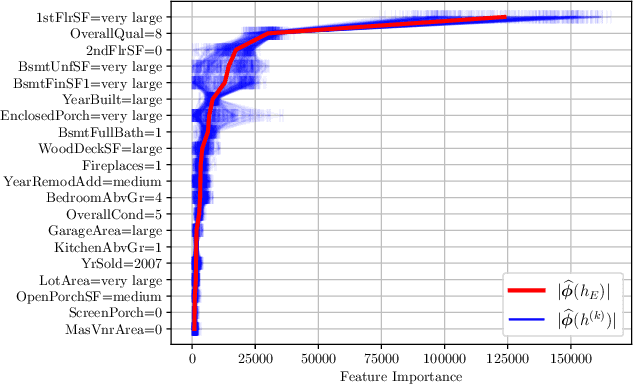
Post-hoc feature importance is progressively being employed to explain decisions of complex machine learning models. Yet in practice, reruns of the training algorithm and/or the explainer can result in contradicting statements of feature importance, henceforth reducing trust in those techniques. A possible avenue to address this issue is to develop strategies to aggregate diverse explanations about feature importance. While the arithmetic mean, which yields a total order, has been advanced, we introduce an alternative: the consensus among multiple models, which results in partial orders. The two aggregation strategies are compared using Integrated Gradients and Shapley values on two regression datasets, and we show that a large portion of the information provided by the mean aggregation is not supported by the consensus of each individual model, raising suspicion on the trustworthiness of this practice.

Generalization Bounds For Meta-Learning: An Information-Theoretic Analysis

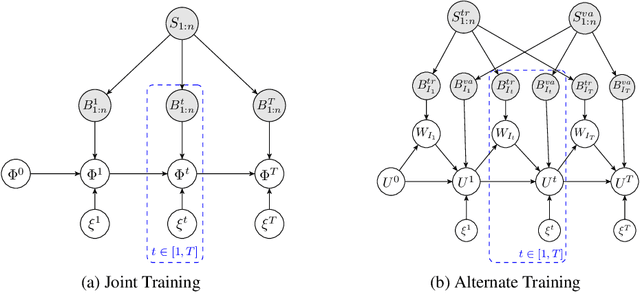
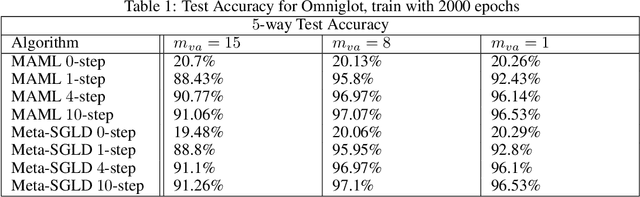
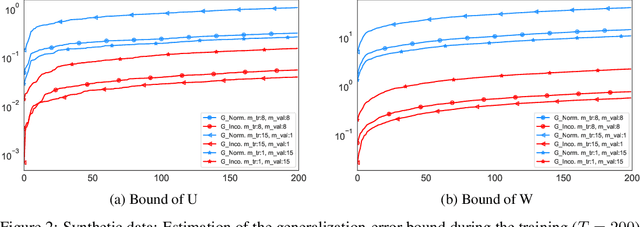
We derive a novel information-theoretic analysis of the generalization property of meta-learning algorithms. Concretely, our analysis proposes a generic understanding of both the conventional learning-to-learn framework and the modern model-agnostic meta-learning (MAML) algorithms. Moreover, we provide a data-dependent generalization bound for a stochastic variant of MAML, which is non-vacuous for deep few-shot learning. As compared to previous bounds that depend on the square norm of gradients, empirical validations on both simulated data and a well-known few-shot benchmark show that our bound is orders of magnitude tighter in most situations.

Decision trees as partitioning machines to characterize their generalization properties

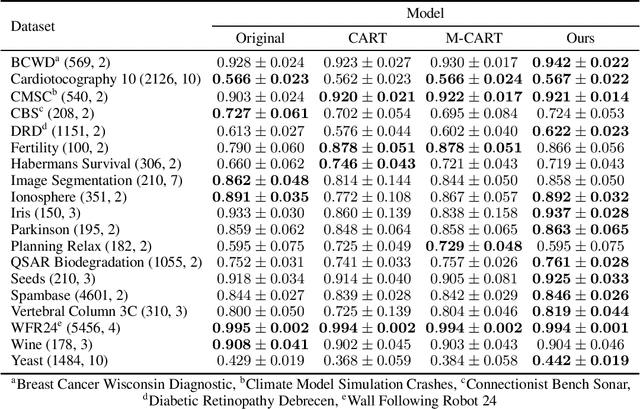
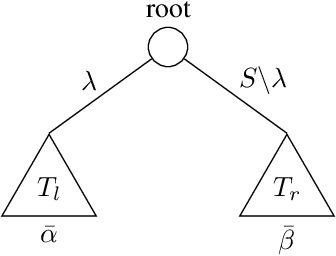
Decision trees are popular machine learning models that are simple to build and easy to interpret. Even though algorithms to learn decision trees date back to almost 50 years, key properties affecting their generalization error are still weakly bounded. Hence, we revisit binary decision trees on real-valued features from the perspective of partitions of the data. We introduce the notion of partitioning function, and we relate it to the growth function and to the VC dimension. Using this new concept, we are able to find the exact VC dimension of decision stumps, which is given by the largest integer $d$ such that $2\ell \ge \binom{d}{\left\lfloor\frac{d}{2}\right\rfloor}$, where $\ell$ is the number of real-valued features. We provide a recursive expression to bound the partitioning functions, resulting in a upper bound on the growth function of any decision tree structure. This allows us to show that the VC dimension of a binary tree structure with $N$ internal nodes is of order $N \log(N\ell)$. Finally, we elaborate a pruning algorithm based on these results that performs better than the CART algorithm on a number of datasets, with the advantage that no cross-validation is required.

Adaptive Deep Kernel Learning

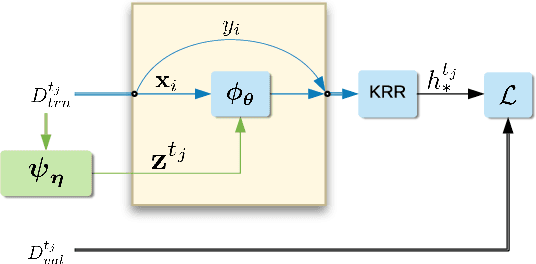
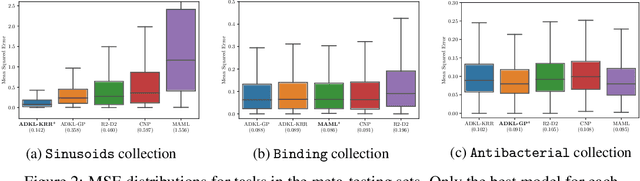
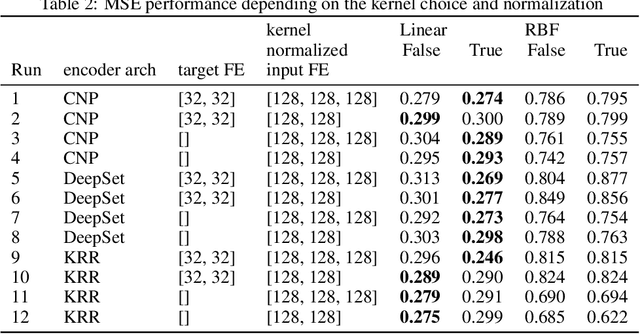
Deep kernel learning provides an elegant and principled framework for combining the structural properties of deep learning algorithms with the flexibility of kernel methods. By means of a deep neural network, it consists of learning a kernel operator which is combined with a differentiable kernel algorithm for inference. While previous work within this framework has mostly explored learning a single kernel for large datasets, we focus herein on learning a kernel family for a variety of tasks in few-shot regression settings. Compared to single deep kernel learning, our novel algorithm permits finding the appropriate kernel for each task during inference, rather than using the same for all tasks. As such, our algorithm performs more effectively with complex task distributions in few-shot learning, which we demonstrate by benchmarking against existing state-of-the-art algorithms using real-world, few-shot regression tasks related to drug discovery.

Large scale modeling of antimicrobial resistance with interpretable classifiers

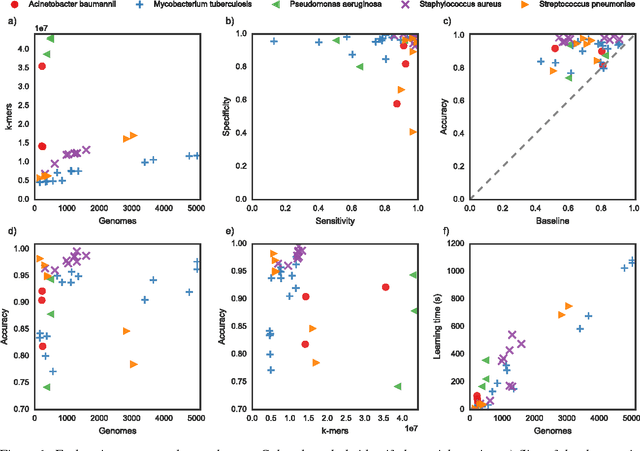
Antimicrobial resistance is an important public health concern that has implications in the practice of medicine worldwide. Accurately predicting resistance phenotypes from genome sequences shows great promise in promoting better use of antimicrobial agents, by determining which antibiotics are likely to be effective in specific clinical cases. In healthcare, this would allow for the design of treatment plans tailored for specific individuals, likely resulting in better clinical outcomes for patients with bacterial infections. In this work, we present the recent work of Drouin et al. (2016) on using Set Covering Machines to learn highly interpretable models of antibiotic resistance and complement it by providing a large scale application of their method to the entire PATRIC database. We report prediction results for 36 new datasets and present the Kover AMR platform, a new web-based tool allowing the visualization and interpretation of the generated models.