Improving Generalization Bounds for VC Classes Using the Hypergeometric Tail Inversion
Paper and Code
Oct 29, 2021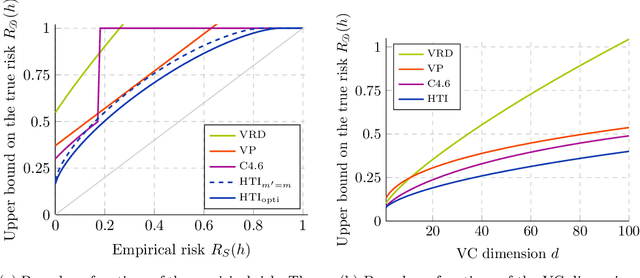
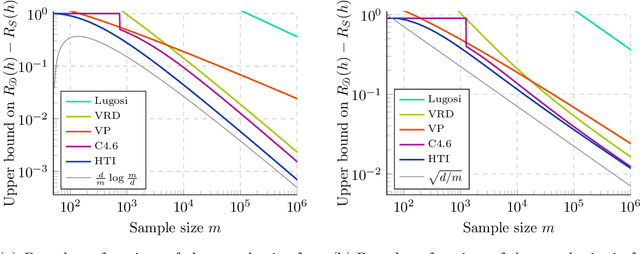
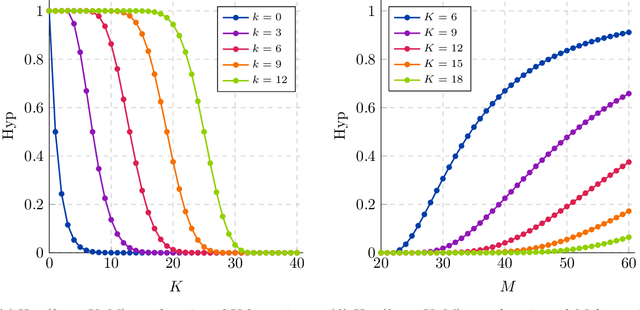
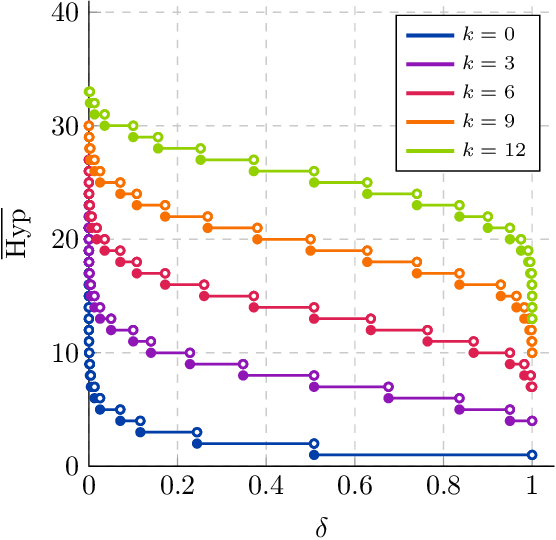
We significantly improve the generalization bounds for VC classes by using two main ideas. First, we consider the hypergeometric tail inversion to obtain a very tight non-uniform distribution-independent risk upper bound for VC classes. Second, we optimize the ghost sample trick to obtain a further non-negligible gain. These improvements are then used to derive a relative deviation bound, a multiclass margin bound, as well as a lower bound. Numerical comparisons show that the new bound is nearly never vacuous, and is tighter than other VC bounds for all reasonable data set sizes.
* 15 pages (body), 36 pages (appendices), 54 pages (total), 13 figures
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge