The geometry of invariant learning: an information-theoretic analysis of data augmentation and generalization

Data augmentation is one of the most widely used techniques to improve generalization in modern machine learning, often justified by its ability to promote invariance to label-irrelevant transformations. However, its theoretical role remains only partially understood. In this work, we propose an information-theoretic framework that systematically accounts for the effect of augmentation on generalization and invariance learning. Our approach builds upon mutual information-based bounds, which relate the generalization gap to the amount of information a learning algorithm retains about its training data. We extend this framework by modeling the augmented distribution as a composition of the original data distribution with a distribution over transformations, which naturally induces an orbit-averaged loss function. Under mild sub-Gaussian assumptions on the loss function and the augmentation process, we derive a new generalization bound that decompose the expected generalization gap into three interpretable terms: (1) a distributional divergence between the original and augmented data, (2) a stability term measuring the algorithm dependence on training data, and (3) a sensitivity term capturing the effect of augmentation variability. To connect our bounds to the geometry of the augmentation group, we introduce the notion of group diameter, defined as the maximal perturbation that augmentations can induce in the input space. The group diameter provides a unified control parameter that bounds all three terms and highlights an intrinsic trade-off: small diameters preserve data fidelity but offer limited regularization, while large diameters enhance stability at the cost of increased bias and sensitivity. We validate our theoretical bounds with numerical experiments, demonstrating that it reliably tracks and predicts the behavior of the true generalization gap.

Tighter Risk Bounds for Mixtures of Experts

In this work, we provide upper bounds on the risk of mixtures of experts by imposing local differential privacy (LDP) on their gating mechanism. These theoretical guarantees are tailored to mixtures of experts that utilize the one-out-of-$n$ gating mechanism, as opposed to the conventional $n$-out-of-$n$ mechanism. The bounds exhibit logarithmic dependence on the number of experts, and encapsulate the dependence on the gating mechanism in the LDP parameter, making them significantly tighter than existing bounds, under reasonable conditions. Experimental results support our theory, demonstrating that our approach enhances the generalization ability of mixtures of experts and validating the feasibility of imposing LDP on the gating mechanism.

Generalization Properties of Decision Trees on Real-valued and Categorical Features

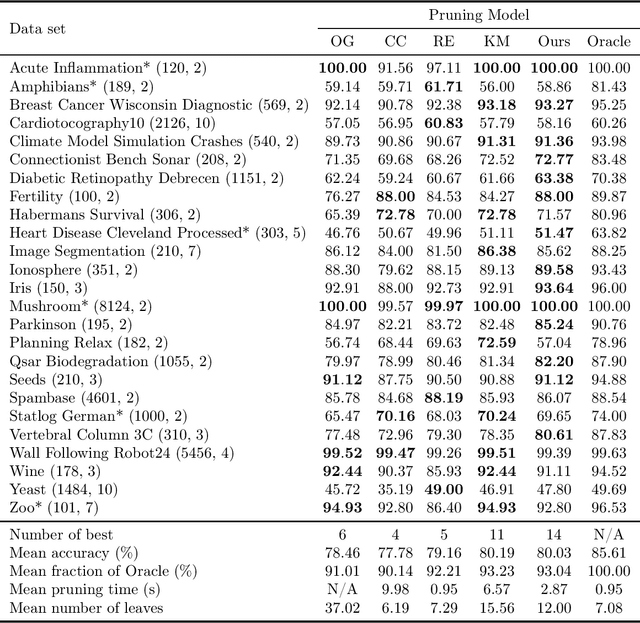
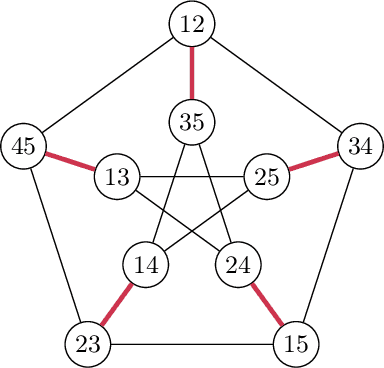
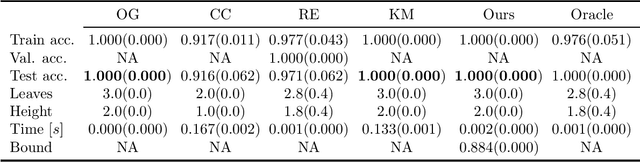
We revisit binary decision trees from the perspective of partitions of the data. We introduce the notion of partitioning function, and we relate it to the growth function and to the VC dimension. We consider three types of features: real-valued, categorical ordinal and categorical nominal, with different split rules for each. For each feature type, we upper bound the partitioning function of the class of decision stumps before extending the bounds to the class of general decision tree (of any fixed structure) using a recursive approach. Using these new results, we are able to find the exact VC dimension of decision stumps on examples of $\ell$ real-valued features, which is given by the largest integer $d$ such that $2\ell \ge \binom{d}{\lfloor\frac{d}{2}\rfloor}$. Furthermore, we show that the VC dimension of a binary tree structure with $L_T$ leaves on examples of $\ell$ real-valued features is in $O(L_T \log(L_T\ell))$. Finally, we elaborate a pruning algorithm based on these results that performs better than the cost-complexity and reduced-error pruning algorithms on a number of data sets, with the advantage that no cross-validation is required.

Improving Generalization Bounds for VC Classes Using the Hypergeometric Tail Inversion

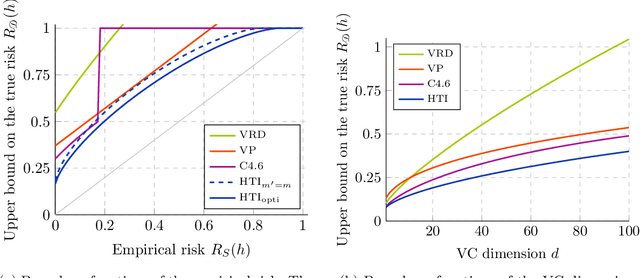
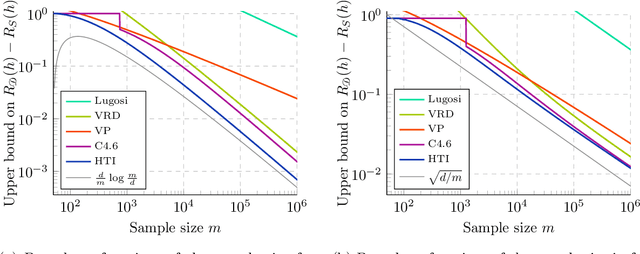
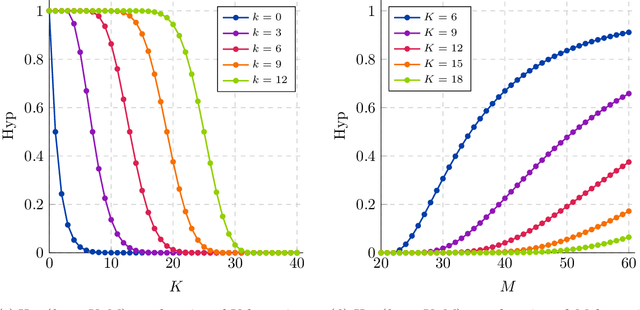
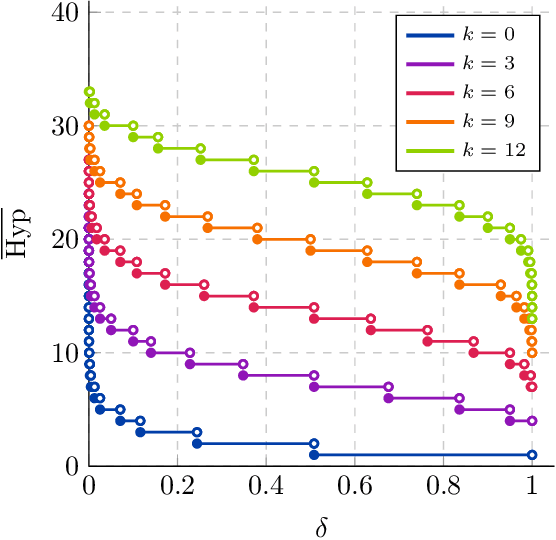
We significantly improve the generalization bounds for VC classes by using two main ideas. First, we consider the hypergeometric tail inversion to obtain a very tight non-uniform distribution-independent risk upper bound for VC classes. Second, we optimize the ghost sample trick to obtain a further non-negligible gain. These improvements are then used to derive a relative deviation bound, a multiclass margin bound, as well as a lower bound. Numerical comparisons show that the new bound is nearly never vacuous, and is tighter than other VC bounds for all reasonable data set sizes.

Decision trees as partitioning machines to characterize their generalization properties

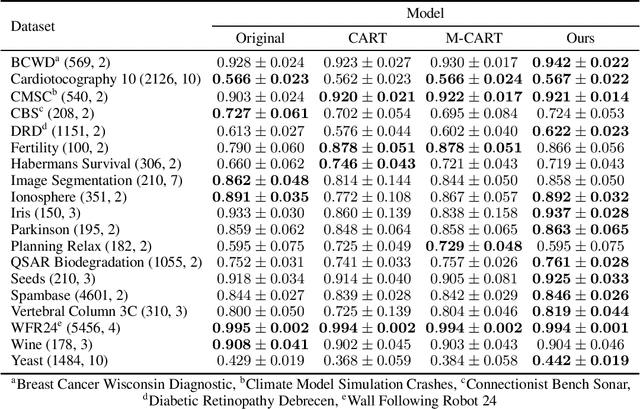
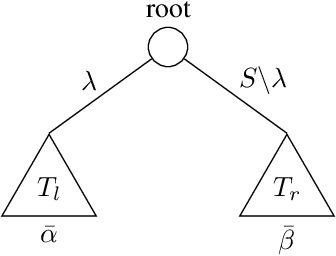
Decision trees are popular machine learning models that are simple to build and easy to interpret. Even though algorithms to learn decision trees date back to almost 50 years, key properties affecting their generalization error are still weakly bounded. Hence, we revisit binary decision trees on real-valued features from the perspective of partitions of the data. We introduce the notion of partitioning function, and we relate it to the growth function and to the VC dimension. Using this new concept, we are able to find the exact VC dimension of decision stumps, which is given by the largest integer $d$ such that $2\ell \ge \binom{d}{\left\lfloor\frac{d}{2}\right\rfloor}$, where $\ell$ is the number of real-valued features. We provide a recursive expression to bound the partitioning functions, resulting in a upper bound on the growth function of any decision tree structure. This allows us to show that the VC dimension of a binary tree structure with $N$ internal nodes is of order $N \log(N\ell)$. Finally, we elaborate a pruning algorithm based on these results that performs better than the CART algorithm on a number of datasets, with the advantage that no cross-validation is required.