Generalization Bounds For Meta-Learning: An Information-Theoretic Analysis
Paper and Code
Sep 29, 2021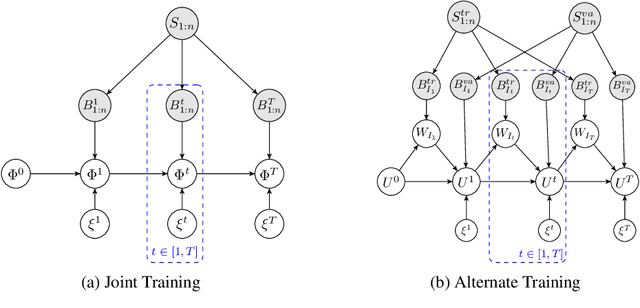
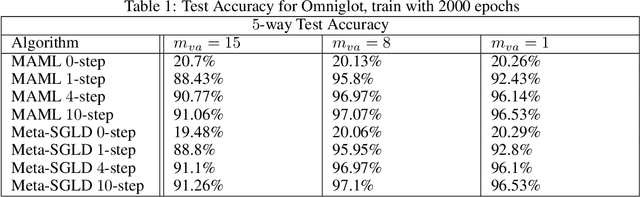
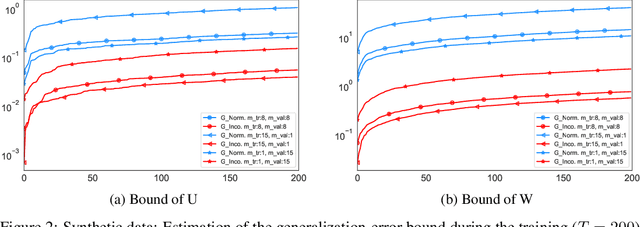
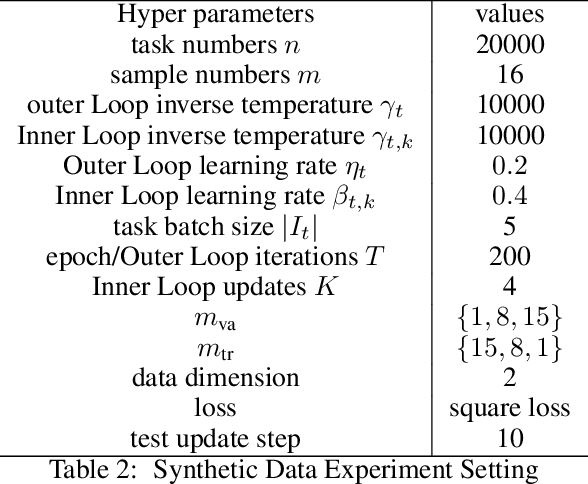
We derive a novel information-theoretic analysis of the generalization property of meta-learning algorithms. Concretely, our analysis proposes a generic understanding of both the conventional learning-to-learn framework and the modern model-agnostic meta-learning (MAML) algorithms. Moreover, we provide a data-dependent generalization bound for a stochastic variant of MAML, which is non-vacuous for deep few-shot learning. As compared to previous bounds that depend on the square norm of gradients, empirical validations on both simulated data and a well-known few-shot benchmark show that our bound is orders of magnitude tighter in most situations.
View paper on
 OpenReview
OpenReview
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge