Improving Out-of-Distribution Detection by Combining Existing Post-hoc Methods

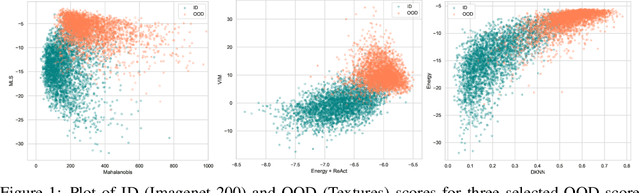
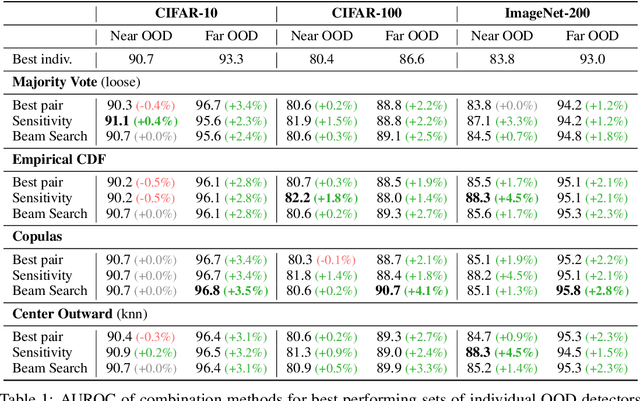
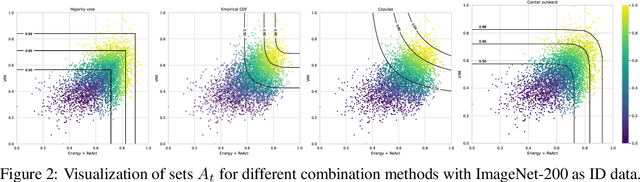
Since the seminal paper of Hendrycks et al. arXiv:1610.02136, Post-hoc deep Out-of-Distribution (OOD) detection has expanded rapidly. As a result, practitioners working on safety-critical applications and seeking to improve the robustness of a neural network now have a plethora of methods to choose from. However, no method outperforms every other on every dataset arXiv:2210.07242, so the current best practice is to test all the methods on the datasets at hand. This paper shifts focus from developing new methods to effectively combining existing ones to enhance OOD detection. We propose and compare four different strategies for integrating multiple detection scores into a unified OOD detector, based on techniques such as majority vote, empirical and copulas-based Cumulative Distribution Function modeling, and multivariate quantiles based on optimal transport. We extend common OOD evaluation metrics -- like AUROC and FPR at fixed TPR rates -- to these multi-dimensional OOD detectors, allowing us to evaluate them and compare them with individual methods on extensive benchmarks. Furthermore, we propose a series of guidelines to choose what OOD detectors to combine in more realistic settings, i.e. in the absence of known OOD data, relying on principles drawn from Outlier Exposure arXiv:1812.04606. The code is available at https://github.com/paulnovello/multi-ood.

Out-of-Distribution Detection Should Use Conformal Prediction (and Vice-versa?)

Research on Out-Of-Distribution (OOD) detection focuses mainly on building scores that efficiently distinguish OOD data from In Distribution (ID) data. On the other hand, Conformal Prediction (CP) uses non-conformity scores to construct prediction sets with probabilistic coverage guarantees. In this work, we propose to use CP to better assess the efficiency of OOD scores. Specifically, we emphasize that in standard OOD benchmark settings, evaluation metrics can be overly optimistic due to the finite sample size of the test dataset. Based on the work of (Bates et al., 2022), we define new conformal AUROC and conformal FRP@TPR95 metrics, which are corrections that provide probabilistic conservativeness guarantees on the variability of these metrics. We show the effect of these corrections on two reference OOD and anomaly detection benchmarks, OpenOOD (Yang et al., 2022) and ADBench (Han et al., 2022). We also show that the benefits of using OOD together with CP apply the other way around by using OOD scores as non-conformity scores, which results in improving upon current CP methods. One of the key messages of these contributions is that since OOD is concerned with designing scores and CP with interpreting these scores, the two fields may be inherently intertwined.

GROOD: GRadient-aware Out-Of-Distribution detection in interpolated manifolds

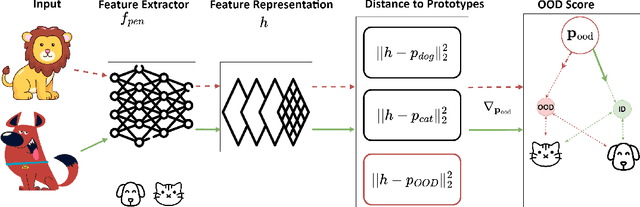
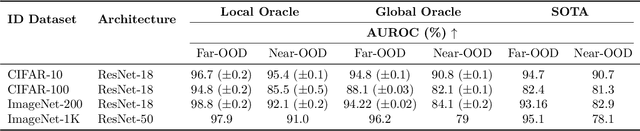
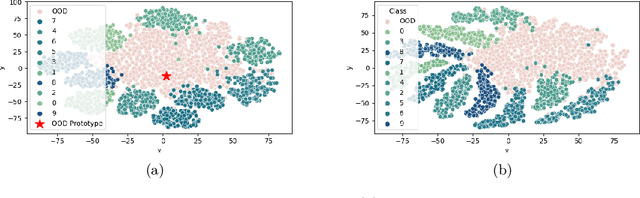
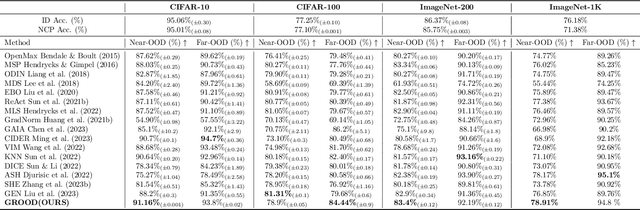
Deep neural networks (DNNs) often fail silently with over-confident predictions on out-of-distribution (OOD) samples, posing risks in real-world deployments. Existing techniques predominantly emphasize either the feature representation space or the gradient norms computed with respect to DNN parameters, yet they overlook the intricate gradient distribution and the topology of classification regions. To address this gap, we introduce GRadient-aware Out-Of-Distribution detection in interpolated manifolds (GROOD), a novel framework that relies on the discriminative power of gradient space to distinguish between in-distribution (ID) and OOD samples. To build this space, GROOD relies on class prototypes together with a prototype that specifically captures OOD characteristics. Uniquely, our approach incorporates a targeted mix-up operation at an early intermediate layer of the DNN to refine the separation of gradient spaces between ID and OOD samples. We quantify OOD detection efficacy using the distance to the nearest neighbor gradients derived from the training set, yielding a robust OOD score. Experimental evaluations substantiate that the introduction of targeted input mix-upamplifies the separation between ID and OOD in the gradient space, yielding impressive results across diverse datasets. Notably, when benchmarked against ImageNet-1k, GROOD surpasses the established robustness of state-of-the-art baselines. Through this work, we establish the utility of leveraging gradient spaces and class prototypes for enhanced OOD detection for DNN in image classification.

Unlocking Feature Visualization for Deeper Networks with MAgnitude Constrained Optimization

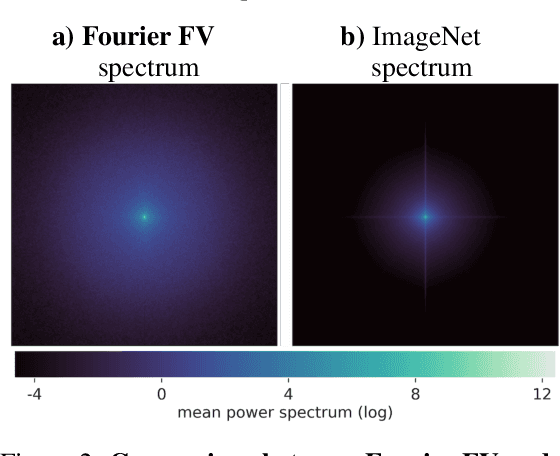
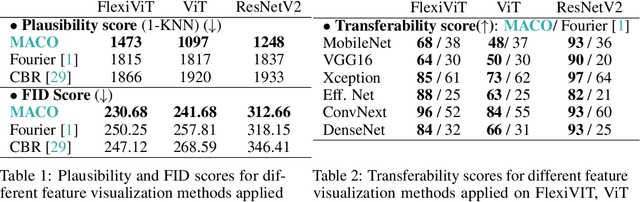
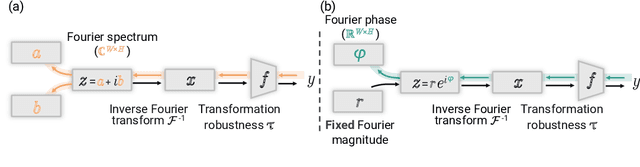
Feature visualization has gained substantial popularity, particularly after the influential work by Olah et al. in 2017, which established it as a crucial tool for explainability. However, its widespread adoption has been limited due to a reliance on tricks to generate interpretable images, and corresponding challenges in scaling it to deeper neural networks. Here, we describe MACO, a simple approach to address these shortcomings. The main idea is to generate images by optimizing the phase spectrum while keeping the magnitude constant to ensure that generated explanations lie in the space of natural images. Our approach yields significantly better results (both qualitatively and quantitatively) and unlocks efficient and interpretable feature visualizations for large state-of-the-art neural networks. We also show that our approach exhibits an attribution mechanism allowing us to augment feature visualizations with spatial importance. We validate our method on a novel benchmark for comparing feature visualization methods, and release its visualizations for all classes of the ImageNet dataset on https://serre-lab.github.io/Lens/. Overall, our approach unlocks, for the first time, feature visualizations for large, state-of-the-art deep neural networks without resorting to any parametric prior image model.

Accelerating hypersonic reentry simulations using deep learning-based hybridization (with guarantees)

In this paper, we are interested in the acceleration of numerical simulations. We focus on a hypersonic planetary reentry problem whose simulation involves coupling fluid dynamics and chemical reactions. Simulating chemical reactions takes most of the computational time but, on the other hand, cannot be avoided to obtain accurate predictions. We face a trade-off between cost-efficiency and accuracy: the simulation code has to be sufficiently efficient to be used in an operational context but accurate enough to predict the phenomenon faithfully. To tackle this trade-off, we design a hybrid simulation code coupling a traditional fluid dynamic solver with a neural network approximating the chemical reactions. We rely on their power in terms of accuracy and dimension reduction when applied in a big data context and on their efficiency stemming from their matrix-vector structure to achieve important acceleration factors ($\times 10$ to $\times 18.6$). This paper aims to explain how we design such cost-effective hybrid simulation codes in practice. Above all, we describe methodologies to ensure accuracy guarantees, allowing us to go beyond traditional surrogate modeling and to use these codes as references.

Goal-Oriented Sensitivity Analysis of Hyperparameters in Deep Learning

Tackling new machine learning problems with neural networks always means optimizing numerous hyperparameters that define their structure and strongly impact their performances. In this work, we study the use of goal-oriented sensitivity analysis, based on the Hilbert-Schmidt Independence Criterion (HSIC), for hyperparameter analysis and optimization. Hyperparameters live in spaces that are often complex and awkward. They can be of different natures (categorical, discrete, boolean, continuous), interact, and have inter-dependencies. All this makes it non-trivial to perform classical sensitivity analysis. We alleviate these difficulties to obtain a robust analysis index that is able to quantify hyperparameters' relative impact on a neural network's final error. This valuable tool allows us to better understand hyperparameters and to make hyperparameter optimization more interpretable. We illustrate the benefits of this knowledge in the context of hyperparameter optimization and derive an HSIC-based optimization algorithm that we apply on MNIST and Cifar, classical machine learning data sets, but also on the approximation of Runge function and Bateman equations solution, of interest for scientific machine learning. This method yields neural networks that are both competitive and cost-effective.

Making Sense of Dependence: Efficient Black-box Explanations Using Dependence Measure

This paper presents a new efficient black-box attribution method based on Hilbert-Schmidt Independence Criterion (HSIC), a dependence measure based on Reproducing Kernel Hilbert Spaces (RKHS). HSIC measures the dependence between regions of an input image and the output of a model based on kernel embeddings of distributions. It thus provides explanations enriched by RKHS representation capabilities. HSIC can be estimated very efficiently, significantly reducing the computational cost compared to other black-box attribution methods. Our experiments show that HSIC is up to 8 times faster than the previous best black-box attribution methods while being as faithful. Indeed, we improve or match the state-of-the-art of both black-box and white-box attribution methods for several fidelity metrics on Imagenet with various recent model architectures. Importantly, we show that these advances can be transposed to efficiently and faithfully explain object detection models such as YOLOv4. Finally, we extend the traditional attribution methods by proposing a new kernel enabling an orthogonal decomposition of importance scores based on HSIC, allowing us to evaluate not only the importance of each image patch but also the importance of their pairwise interactions.

Variance Based Samples Weighting for Supervised Deep Learning

In the context of supervised learning of a function by a Neural Network (NN), we claim and empirically justify that a NN yields better results when the distribution of the data set focuses on regions where the function to learn is steeper. We first traduce this assumption in a mathematically workable way using Taylor expansion. Then, theoretical derivations allow to construct a methodology that we call Variance Based Samples Weighting (VBSW). VBSW uses local variance of the labels to weight the training points. This methodology is general, scalable, cost effective, and significantly increases the performances of a large class of NNs for various classification and regression tasks on image, text and multivariate data. We highlight its benefits with experiments involving NNs from shallow linear NN to Resnet or Bert.

A Taylor Based Sampling Scheme for Machine Learning in Computational Physics

Machine Learning (ML) is increasingly used to construct surrogate models for physical simulations. We take advantage of the ability to generate data using numerical simulations programs to train ML models better and achieve accuracy gain with no performance cost. We elaborate a new data sampling scheme based on Taylor approximation to reduce the error of a Deep Neural Network (DNN) when learning the solution of an ordinary differential equations (ODE) system.