DP-SGD Without Clipping: The Lipschitz Neural Network Way

State-of-the-art approaches for training Differentially Private (DP) Deep Neural Networks (DNN) faces difficulties to estimate tight bounds on the sensitivity of the network's layers, and instead rely on a process of per-sample gradient clipping. This clipping process not only biases the direction of gradients but also proves costly both in memory consumption and in computation. To provide sensitivity bounds and bypass the drawbacks of the clipping process, our theoretical analysis of Lipschitz constrained networks reveals an unexplored link between the Lipschitz constant with respect to their input and the one with respect to their parameters. By bounding the Lipschitz constant of each layer with respect to its parameters we guarantee DP training of these networks. This analysis not only allows the computation of the aforementioned sensitivities at scale but also provides leads on to how maximize the gradient-to-noise ratio for fixed privacy guarantees. To facilitate the application of Lipschitz networks and foster robust and certifiable learning under privacy guarantees, we provide a Python package that implements building blocks allowing the construction and private training of such networks.

From Noisy Fixed-Point Iterations to Private ADMM for Centralized and Federated Learning

We study differentially private (DP) machine learning algorithms as instances of noisy fixed-point iterations, in order to derive privacy and utility results from this well-studied framework. We show that this new perspective recovers popular private gradient-based methods like DP-SGD and provides a principled way to design and analyze new private optimization algorithms in a flexible manner. Focusing on the widely-used Alternating Directions Method of Multipliers (ADMM) method, we use our general framework to derive novel private ADMM algorithms for centralized, federated and fully decentralized learning. For these three algorithms, we establish strong privacy guarantees leveraging privacy amplification by iteration and by subsampling. Finally, we provide utility guarantees using a unified analysis that exploits a recent linear convergence result for noisy fixed-point iterations.

A Comparison between Deep Neural Nets and Kernel Acoustic Models for Speech Recognition

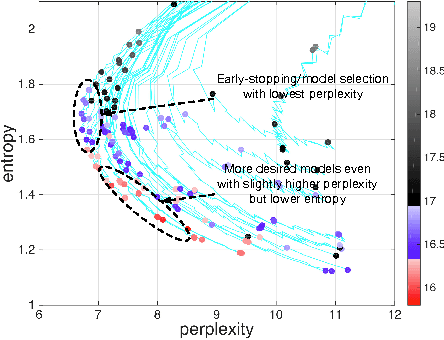
We study large-scale kernel methods for acoustic modeling and compare to DNNs on performance metrics related to both acoustic modeling and recognition. Measuring perplexity and frame-level classification accuracy, kernel-based acoustic models are as effective as their DNN counterparts. However, on token-error-rates DNN models can be significantly better. We have discovered that this might be attributed to DNN's unique strength in reducing both the perplexity and the entropy of the predicted posterior probabilities. Motivated by our findings, we propose a new technique, entropy regularized perplexity, for model selection. This technique can noticeably improve the recognition performance of both types of models, and reduces the gap between them. While effective on Broadcast News, this technique could be also applicable to other tasks.

Similarity Learning for Provably Accurate Sparse Linear Classification

In recent years, the crucial importance of metrics in machine learning algorithms has led to an increasing interest for optimizing distance and similarity functions. Most of the state of the art focus on learning Mahalanobis distances (requiring to fulfill a constraint of positive semi-definiteness) for use in a local k-NN algorithm. However, no theoretical link is established between the learned metrics and their performance in classification. In this paper, we make use of the formal framework of good similarities introduced by Balcan et al. to design an algorithm for learning a non PSD linear similarity optimized in a nonlinear feature space, which is then used to build a global linear classifier. We show that our approach has uniform stability and derive a generalization bound on the classification error. Experiments performed on various datasets confirm the effectiveness of our approach compared to state-of-the-art methods and provide evidence that (i) it is fast, (ii) robust to overfitting and (iii) produces very sparse classifiers.