Optimal Classification under Performative Distribution Shift

Performative learning addresses the increasingly pervasive situations in which algorithmic decisions may induce changes in the data distribution as a consequence of their public deployment. We propose a novel view in which these performative effects are modelled as push-forward measures. This general framework encompasses existing models and enables novel performative gradient estimation methods, leading to more efficient and scalable learning strategies. For distribution shifts, unlike previous models which require full specification of the data distribution, we only assume knowledge of the shift operator that represents the performative changes. This approach can also be integrated into various change-of-variablebased models, such as VAEs or normalizing flows. Focusing on classification with a linear-in-parameters performative effect, we prove the convexity of the performative risk under a new set of assumptions. Notably, we do not limit the strength of performative effects but rather their direction, requiring only that classification becomes harder when deploying more accurate models. In this case, we also establish a connection with adversarially robust classification by reformulating the minimization of the performative risk as a min-max variational problem. Finally, we illustrate our approach on synthetic and real datasets.

Privacy Attacks in Decentralized Learning

Decentralized Gradient Descent (D-GD) allows a set of users to perform collaborative learning without sharing their data by iteratively averaging local model updates with their neighbors in a network graph. The absence of direct communication between non-neighbor nodes might lead to the belief that users cannot infer precise information about the data of others. In this work, we demonstrate the opposite, by proposing the first attack against D-GD that enables a user (or set of users) to reconstruct the private data of other users outside their immediate neighborhood. Our approach is based on a reconstruction attack against the gossip averaging protocol, which we then extend to handle the additional challenges raised by D-GD. We validate the effectiveness of our attack on real graphs and datasets, showing that the number of users compromised by a single or a handful of attackers is often surprisingly large. We empirically investigate some of the factors that affect the performance of the attack, namely the graph topology, the number of attackers, and their position in the graph.

Differentially Private Decentralized Learning with Random Walks

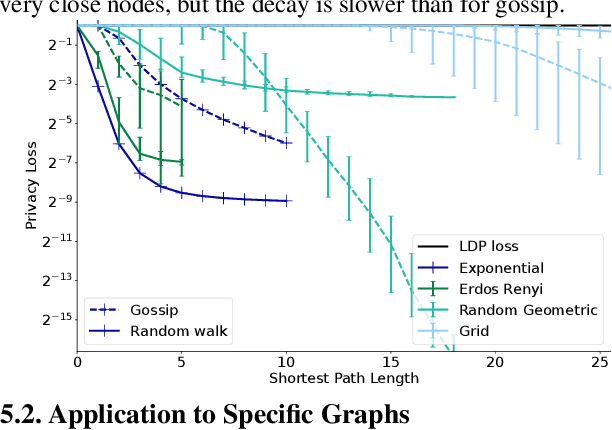
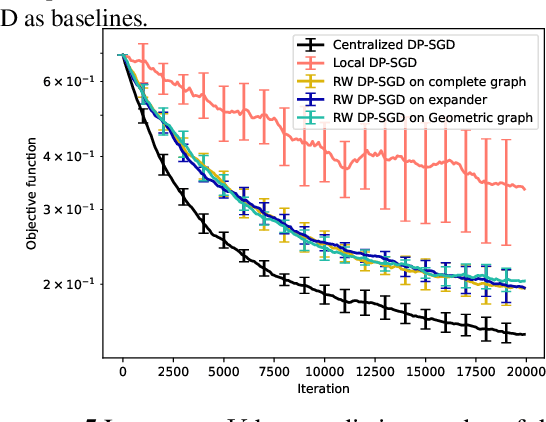
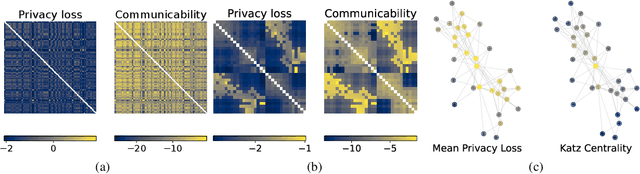
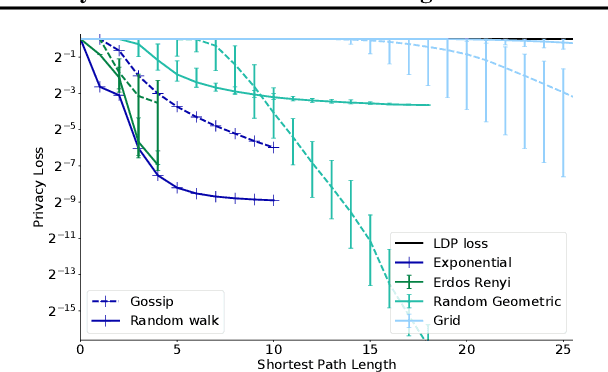
The popularity of federated learning comes from the possibility of better scalability and the ability for participants to keep control of their data, improving data security and sovereignty. Unfortunately, sharing model updates also creates a new privacy attack surface. In this work, we characterize the privacy guarantees of decentralized learning with random walk algorithms, where a model is updated by traveling from one node to another along the edges of a communication graph. Using a recent variant of differential privacy tailored to the study of decentralized algorithms, namely Pairwise Network Differential Privacy, we derive closed-form expressions for the privacy loss between each pair of nodes where the impact of the communication topology is captured by graph theoretic quantities. Our results further reveal that random walk algorithms tends to yield better privacy guarantees than gossip algorithms for nodes close from each other. We supplement our theoretical results with empirical evaluation on synthetic and real-world graphs and datasets.

From Noisy Fixed-Point Iterations to Private ADMM for Centralized and Federated Learning

We study differentially private (DP) machine learning algorithms as instances of noisy fixed-point iterations, in order to derive privacy and utility results from this well-studied framework. We show that this new perspective recovers popular private gradient-based methods like DP-SGD and provides a principled way to design and analyze new private optimization algorithms in a flexible manner. Focusing on the widely-used Alternating Directions Method of Multipliers (ADMM) method, we use our general framework to derive novel private ADMM algorithms for centralized, federated and fully decentralized learning. For these three algorithms, we establish strong privacy guarantees leveraging privacy amplification by iteration and by subsampling. Finally, we provide utility guarantees using a unified analysis that exploits a recent linear convergence result for noisy fixed-point iterations.

FLamby: Datasets and Benchmarks for Cross-Silo Federated Learning in Realistic Healthcare Settings

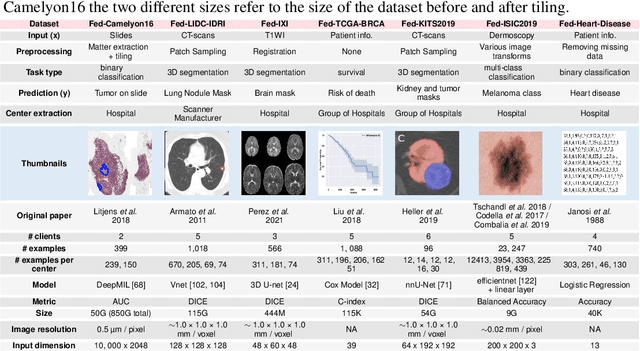
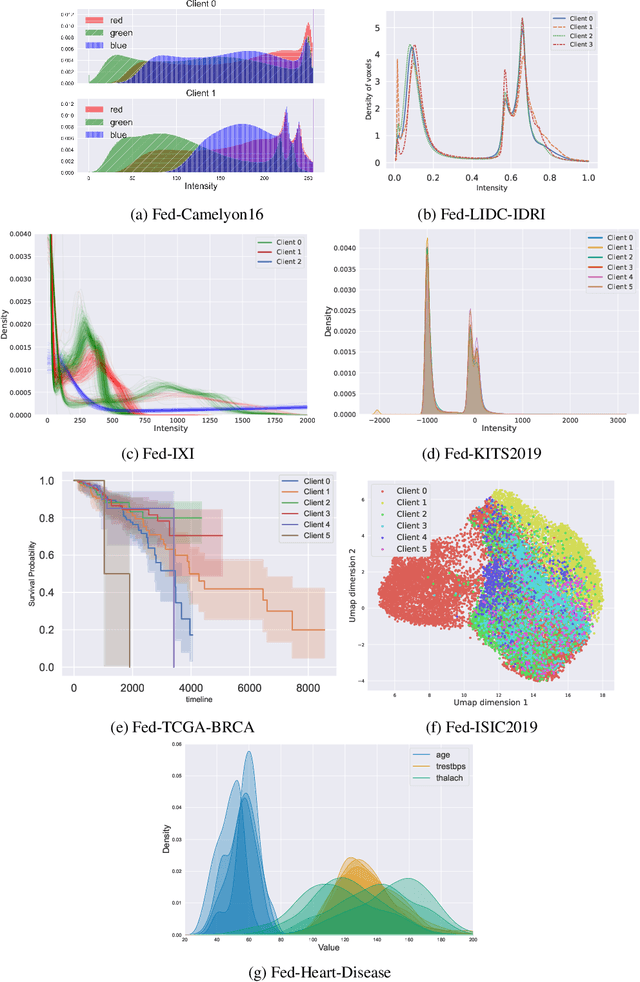
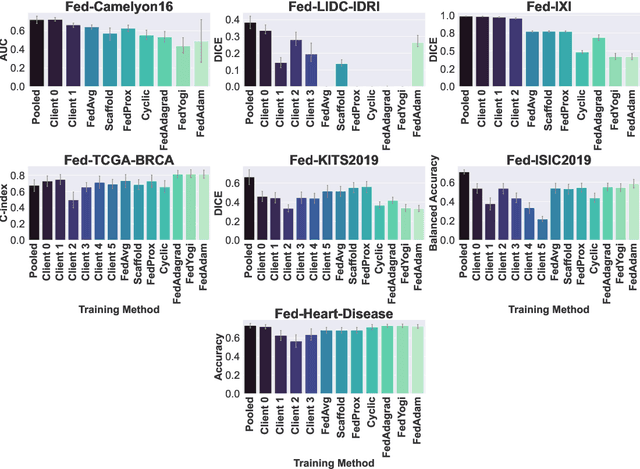
Federated Learning (FL) is a novel approach enabling several clients holding sensitive data to collaboratively train machine learning models, without centralizing data. The cross-silo FL setting corresponds to the case of few ($2$--$50$) reliable clients, each holding medium to large datasets, and is typically found in applications such as healthcare, finance, or industry. While previous works have proposed representative datasets for cross-device FL, few realistic healthcare cross-silo FL datasets exist, thereby slowing algorithmic research in this critical application. In this work, we propose a novel cross-silo dataset suite focused on healthcare, FLamby (Federated Learning AMple Benchmark of Your cross-silo strategies), to bridge the gap between theory and practice of cross-silo FL. FLamby encompasses 7 healthcare datasets with natural splits, covering multiple tasks, modalities, and data volumes, each accompanied with baseline training code. As an illustration, we additionally benchmark standard FL algorithms on all datasets. Our flexible and modular suite allows researchers to easily download datasets, reproduce results and re-use the different components for their research. FLamby is available at~\url{www.github.com/owkin/flamby}.

Muffliato: Peer-to-Peer Privacy Amplification for Decentralized Optimization and Averaging

Decentralized optimization is increasingly popular in machine learning for its scalability and efficiency. Intuitively, it should also provide better privacy guarantees, as nodes only observe the messages sent by their neighbors in the network graph. But formalizing and quantifying this gain is challenging: existing results are typically limited to Local Differential Privacy (LDP) guarantees that overlook the advantages of decentralization. In this work, we introduce pairwise network differential privacy, a relaxation of LDP that captures the fact that the privacy leakage from a node $u$ to a node $v$ may depend on their relative position in the graph. We then analyze the combination of local noise injection with (simple or randomized) gossip averaging protocols on fixed and random communication graphs. We also derive a differentially private decentralized optimization algorithm that alternates between local gradient descent steps and gossip averaging. Our results show that our algorithms amplify privacy guarantees as a function of the distance between nodes in the graph, matching the privacy-utility trade-off of the trusted curator, up to factors that explicitly depend on the graph topology. Finally, we illustrate our privacy gains with experiments on synthetic and real-world datasets.

Privacy Amplification by Decentralization

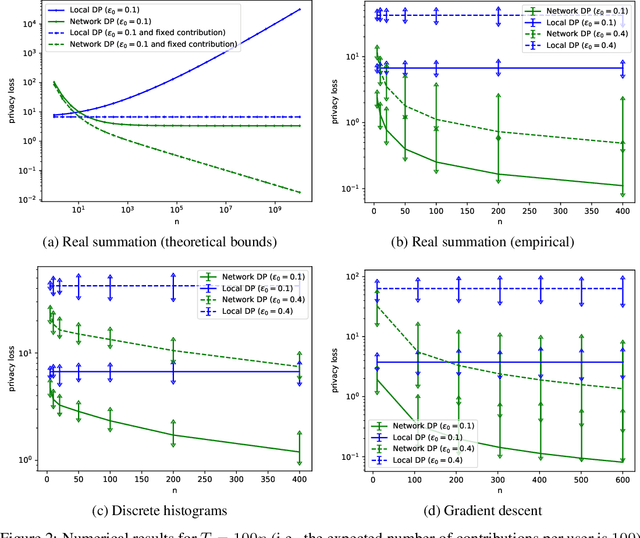
Analyzing data owned by several parties while achieving a good trade-off between utility and privacy is a key challenge in federated learning and analytics. In this work, we introduce a novel relaxation of local differential privacy (LDP) that naturally arises in fully decentralized protocols, i.e. participants exchange information by communicating along the edges of a network graph. This relaxation, that we call network DP, captures the fact that users have only a local view of the decentralized system. To show the relevance of network DP, we study a decentralized model of computation where a token performs a walk on the network graph and is updated sequentially by the party who receives it. For tasks such as real summation, histogram computation and gradient descent, we propose simple algorithms and prove privacy amplification results on ring and complete topologies. The resulting privacy-utility trade-off significantly improves upon LDP, and in some cases even matches what can be achieved with approaches based on secure aggregation and secure shuffling. Our experiments confirm the practical significance of the gains compared to LDP.