Unveiling the Role of Randomization in Multiclass Adversarial Classification: Insights from Graph Theory

Randomization as a mean to improve the adversarial robustness of machine learning models has recently attracted significant attention. Unfortunately, much of the theoretical analysis so far has focused on binary classification, providing only limited insights into the more complex multiclass setting. In this paper, we take a step toward closing this gap by drawing inspiration from the field of graph theory. Our analysis focuses on discrete data distributions, allowing us to cast the adversarial risk minimization problems within the well-established framework of set packing problems. By doing so, we are able to identify three structural conditions on the support of the data distribution that are necessary for randomization to improve robustness. Furthermore, we are able to construct several data distributions where (contrarily to binary classification) switching from a deterministic to a randomized solution significantly reduces the optimal adversarial risk. These findings highlight the crucial role randomization can play in enhancing robustness to adversarial attacks in multiclass classification.

Memorization in Attention-only Transformers

Recent research has explored the memorization capacity of multi-head attention, but these findings are constrained by unrealistic limitations on the context size. We present a novel proof for language-based Transformers that extends the current hypothesis to any context size. Our approach improves upon the state-of-the-art by achieving more effective exact memorization with an attention layer, while also introducing the concept of approximate memorization of distributions. Through experimental validation, we demonstrate that our proposed bounds more accurately reflect the true memorization capacity of language models, and provide a precise comparison with prior work.

Optimal Classification under Performative Distribution Shift

Performative learning addresses the increasingly pervasive situations in which algorithmic decisions may induce changes in the data distribution as a consequence of their public deployment. We propose a novel view in which these performative effects are modelled as push-forward measures. This general framework encompasses existing models and enables novel performative gradient estimation methods, leading to more efficient and scalable learning strategies. For distribution shifts, unlike previous models which require full specification of the data distribution, we only assume knowledge of the shift operator that represents the performative changes. This approach can also be integrated into various change-of-variablebased models, such as VAEs or normalizing flows. Focusing on classification with a linear-in-parameters performative effect, we prove the convexity of the performative risk under a new set of assumptions. Notably, we do not limit the strength of performative effects but rather their direction, requiring only that classification becomes harder when deploying more accurate models. In this case, we also establish a connection with adversarially robust classification by reformulating the minimization of the performative risk as a min-max variational problem. Finally, we illustrate our approach on synthetic and real datasets.

Optimal Budgeted Rejection Sampling for Generative Models

Rejection sampling methods have recently been proposed to improve the performance of discriminator-based generative models. However, these methods are only optimal under an unlimited sampling budget, and are usually applied to a generator trained independently of the rejection procedure. We first propose an Optimal Budgeted Rejection Sampling (OBRS) scheme that is provably optimal with respect to \textit{any} $f$-divergence between the true distribution and the post-rejection distribution, for a given sampling budget. Second, we propose an end-to-end method that incorporates the sampling scheme into the training procedure to further enhance the model's overall performance. Through experiments and supporting theory, we show that the proposed methods are effective in significantly improving the quality and diversity of the samples.

Precision-Recall Divergence Optimization for Generative Modeling with GANs and Normalizing Flows

Achieving a balance between image quality (precision) and diversity (recall) is a significant challenge in the domain of generative models. Current state-of-the-art models primarily rely on optimizing heuristics, such as the Fr\'echet Inception Distance. While recent developments have introduced principled methods for evaluating precision and recall, they have yet to be successfully integrated into the training of generative models. Our main contribution is a novel training method for generative models, such as Generative Adversarial Networks and Normalizing Flows, which explicitly optimizes a user-defined trade-off between precision and recall. More precisely, we show that achieving a specified precision-recall trade-off corresponds to minimizing a unique $f$-divergence from a family we call the \mbox{\em PR-divergences}. Conversely, any $f$-divergence can be written as a linear combination of PR-divergences and corresponds to a weighted precision-recall trade-off. Through comprehensive evaluations, we show that our approach improves the performance of existing state-of-the-art models like BigGAN in terms of either precision or recall when tested on datasets such as ImageNet.

Training Normalizing Flows with the Precision-Recall Divergence

Generative models can have distinct mode of failures like mode dropping and low quality samples, which cannot be captured by a single scalar metric. To address this, recent works propose evaluating generative models using precision and recall, where precision measures quality of samples and recall measures the coverage of the target distribution. Although a variety of discrepancy measures between the target and estimated distribution are used to train generative models, it is unclear what precision-recall trade-offs are achieved by various choices of the discrepancy measures. In this paper, we show that achieving a specified precision-recall trade-off corresponds to minimising -divergences from a family we call the {\em PR-divergences }. Conversely, any -divergence can be written as a linear combination of PR-divergences and therefore correspond to minimising a weighted precision-recall trade-off. Further, we propose a novel generative model that is able to train a normalizing flow to minimise any -divergence, and in particular, achieve a given precision-recall trade-off.

Robust empirical risk minimization via Newton's method

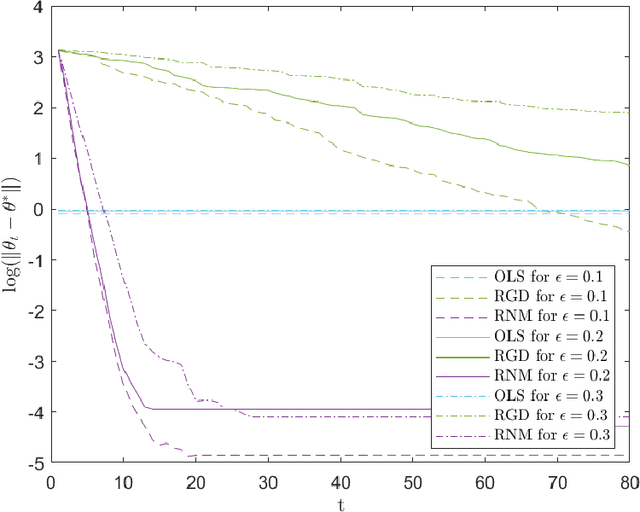
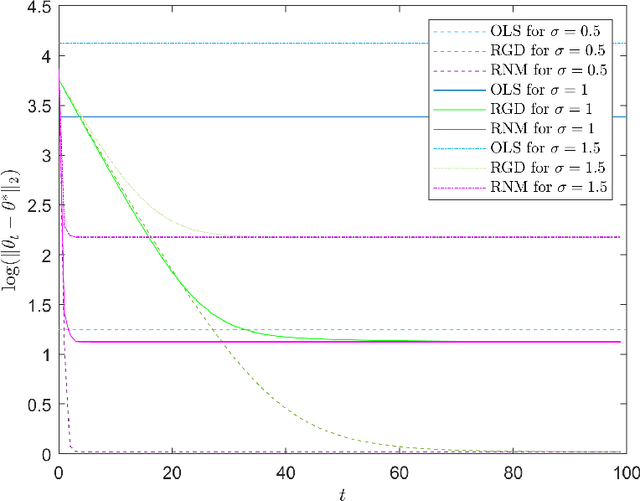
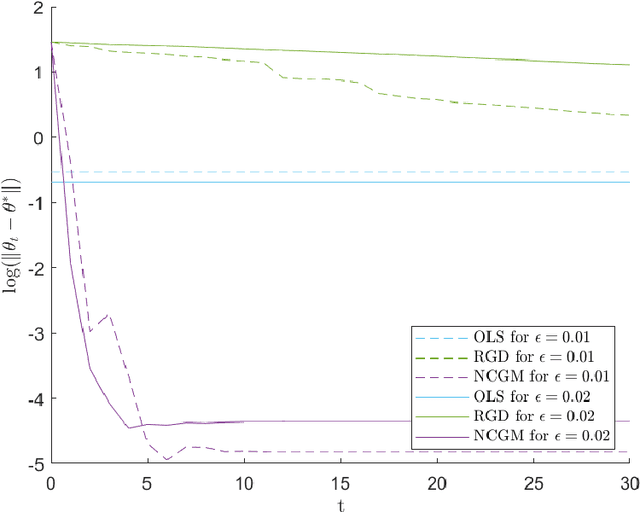
We study a variant of Newton's method for empirical risk minimization, where at each iteration of the optimization algorithm, we replace the gradient and Hessian of the objective function by robust estimators taken from existing literature on robust mean estimation for multivariate data. After proving a general theorem about the convergence of successive iterates to a small ball around the population-level minimizer, we study consequences of our theory in generalized linear models, when data are generated from Huber's epsilon-contamination model and/or heavy-tailed distributions. We also propose an algorithm for obtaining robust Newton directions based on the conjugate gradient method, which may be more appropriate for high-dimensional settings, and provide conjectures about the convergence of the resulting algorithm. Compared to the robust gradient descent algorithm proposed by Prasad et al. (2020), our algorithm enjoys the faster rates of convergence for successive iterates often achieved by second-order algorithms for convex problems, i.e., quadratic convergence in a neighborhood of the optimum, with a stepsize that may be chosen adaptively via backtracking linesearch.

The Many Faces of Adversarial Risk

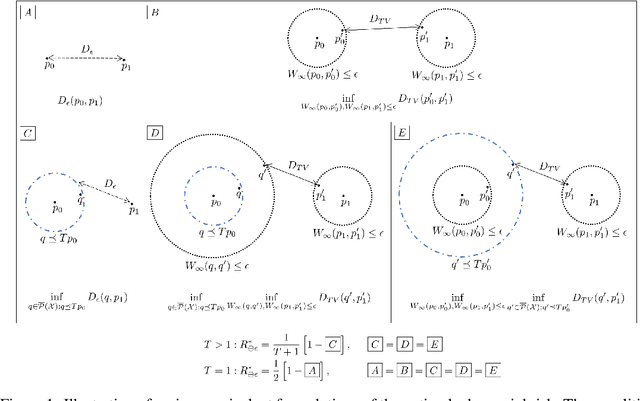
Adversarial risk quantifies the performance of classifiers on adversarially perturbed data. Numerous definitions of adversarial risk -- not all mathematically rigorous and differing subtly in the details -- have appeared in the literature. In this paper, we revisit these definitions, make them rigorous, and critically examine their similarities and differences. Our technical tools derive from optimal transport, robust statistics, functional analysis, and game theory. Our contributions include the following: generalizing Strassen's theorem to the unbalanced optimal transport setting with applications to adversarial classification with unequal priors; showing an equivalence between adversarial robustness and robust hypothesis testing with $\infty$-Wasserstein uncertainty sets; proving the existence of a pure Nash equilibrium in the two-player game between the adversary and the algorithm; and characterizing adversarial risk by the minimum Bayes error between a pair of distributions belonging to the $\infty$-Wasserstein uncertainty sets. Our results generalize and deepen recently discovered connections between optimal transport and adversarial robustness and reveal new connections to Choquet capacities and game theory.

Adversarial Risk via Optimal Transport and Optimal Couplings

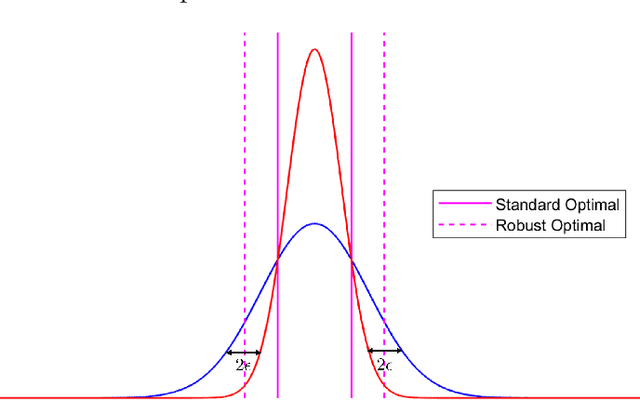
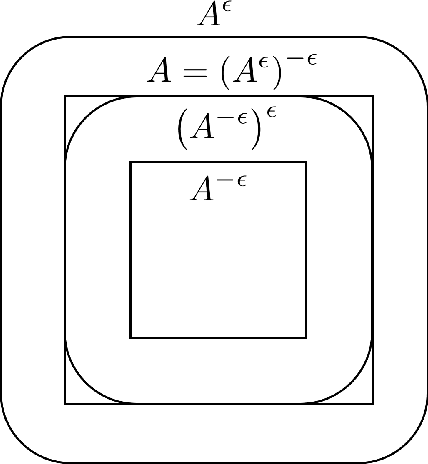
The accuracy of modern machine learning algorithms deteriorates severely on adversarially manipulated test data. Optimal adversarial risk quantifies the best error rate of any classifier in the presence of adversaries, and optimal adversarial classifiers are sought that minimize adversarial risk. In this paper, we investigate the optimal adversarial risk and optimal adversarial classifiers from an optimal transport perspective. We present a new and simple approach to show that the optimal adversarial risk for binary classification with $0-1$ loss function is completely characterized by an optimal transport cost between the probability distributions of the two classes, for a suitably defined cost function. We propose a novel coupling strategy that achieves the optimal transport cost for several univariate distributions like Gaussian, uniform and triangular. Using the optimal couplings, we obtain the optimal adversarial classifiers in these settings and show how they differ from optimal classifiers in the absence of adversaries. Based on our analysis, we evaluate algorithm-independent fundamental limits on adversarial risk for CIFAR-10, MNIST, Fashion-MNIST and SVHN datasets, and Gaussian mixtures based on them. In addition to the $0-1$ loss, we also derive bounds on the deviation of optimal risk and optimal classifier in the presence of adversaries for continuous loss functions, that are based on the convexity and smoothness of the loss functions.

Active Learning with Importance Sampling

We consider an active learning setting where the algorithm has access to a large pool of unlabeled data and a small pool of labeled data. In each iteration, the algorithm chooses few unlabeled data points and obtains their labels from an oracle. In this paper, we consider a probabilistic querying procedure to choose the points to be labeled. We propose an algorithm for Active Learning with Importance Sampling (ALIS), and derive upper bounds on the true loss incurred by the algorithm for any arbitrary probabilistic sampling procedure. Further, we propose an optimal sampling distribution that minimizes the upper bound on the true loss.