The Sample Complexity of Simple Binary Hypothesis Testing

The sample complexity of simple binary hypothesis testing is the smallest number of i.i.d. samples required to distinguish between two distributions $p$ and $q$ in either: (i) the prior-free setting, with type-I error at most $\alpha$ and type-II error at most $\beta$; or (ii) the Bayesian setting, with Bayes error at most $\delta$ and prior distribution $(\alpha, 1-\alpha)$. This problem has only been studied when $\alpha = \beta$ (prior-free) or $\alpha = 1/2$ (Bayesian), and the sample complexity is known to be characterized by the Hellinger divergence between $p$ and $q$, up to multiplicative constants. In this paper, we derive a formula that characterizes the sample complexity (up to multiplicative constants that are independent of $p$, $q$, and all error parameters) for: (i) all $0 \le \alpha, \beta \le 1/8$ in the prior-free setting; and (ii) all $\delta \le \alpha/4$ in the Bayesian setting. In particular, the formula admits equivalent expressions in terms of certain divergences from the Jensen--Shannon and Hellinger families. The main technical result concerns an $f$-divergence inequality between members of the Jensen--Shannon and Hellinger families, which is proved by a combination of information-theoretic tools and case-by-case analyses. We explore applications of our results to robust and distributed (locally-private and communication-constrained) hypothesis testing.

Simple Binary Hypothesis Testing under Local Differential Privacy and Communication Constraints

We study simple binary hypothesis testing under both local differential privacy (LDP) and communication constraints. We qualify our results as either minimax optimal or instance optimal: the former hold for the set of distribution pairs with prescribed Hellinger divergence and total variation distance, whereas the latter hold for specific distribution pairs. For the sample complexity of simple hypothesis testing under pure LDP constraints, we establish instance-optimal bounds for distributions with binary support; minimax-optimal bounds for general distributions; and (approximately) instance-optimal, computationally efficient algorithms for general distributions. When both privacy and communication constraints are present, we develop instance-optimal, computationally efficient algorithms that achieve the minimum possible sample complexity (up to universal constants). Our results on instance-optimal algorithms hinge on identifying the extreme points of the joint range set $\mathcal A$ of two distributions $p$ and $q$, defined as $\mathcal A := \{(\mathbf T p, \mathbf T q) | \mathbf T \in \mathcal C\}$, where $\mathcal C$ is the set of channels characterizing the constraints.

Communication-constrained hypothesis testing: Optimality, robustness, and reverse data processing inequalities

We study hypothesis testing under communication constraints, where each sample is quantized before being revealed to a statistician. Without communication constraints, it is well known that the sample complexity of simple binary hypothesis testing is characterized by the Hellinger distance between the distributions. We show that the sample complexity of simple binary hypothesis testing under communication constraints is at most a logarithmic factor larger than in the unconstrained setting and this bound is tight. We develop a polynomial-time algorithm that achieves the aforementioned sample complexity. Our framework extends to robust hypothesis testing, where the distributions are corrupted in the total variation distance. Our proofs rely on a new reverse data processing inequality and a reverse Markov inequality, which may be of independent interest. For simple $M$-ary hypothesis testing, the sample complexity in the absence of communication constraints has a logarithmic dependence on $M$. We show that communication constraints can cause an exponential blow-up leading to $\Omega(M)$ sample complexity even for adaptive algorithms.

The Many Faces of Adversarial Risk

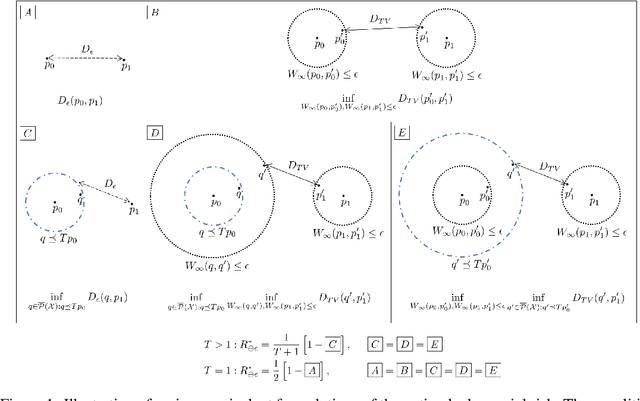
Adversarial risk quantifies the performance of classifiers on adversarially perturbed data. Numerous definitions of adversarial risk -- not all mathematically rigorous and differing subtly in the details -- have appeared in the literature. In this paper, we revisit these definitions, make them rigorous, and critically examine their similarities and differences. Our technical tools derive from optimal transport, robust statistics, functional analysis, and game theory. Our contributions include the following: generalizing Strassen's theorem to the unbalanced optimal transport setting with applications to adversarial classification with unequal priors; showing an equivalence between adversarial robustness and robust hypothesis testing with $\infty$-Wasserstein uncertainty sets; proving the existence of a pure Nash equilibrium in the two-player game between the adversary and the algorithm; and characterizing adversarial risk by the minimum Bayes error between a pair of distributions belonging to the $\infty$-Wasserstein uncertainty sets. Our results generalize and deepen recently discovered connections between optimal transport and adversarial robustness and reveal new connections to Choquet capacities and game theory.

Robust regression with covariate filtering: Heavy tails and adversarial contamination

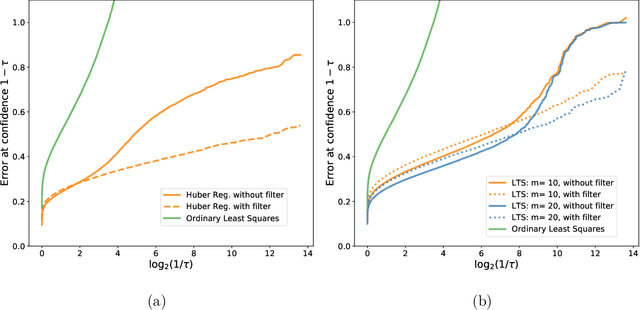
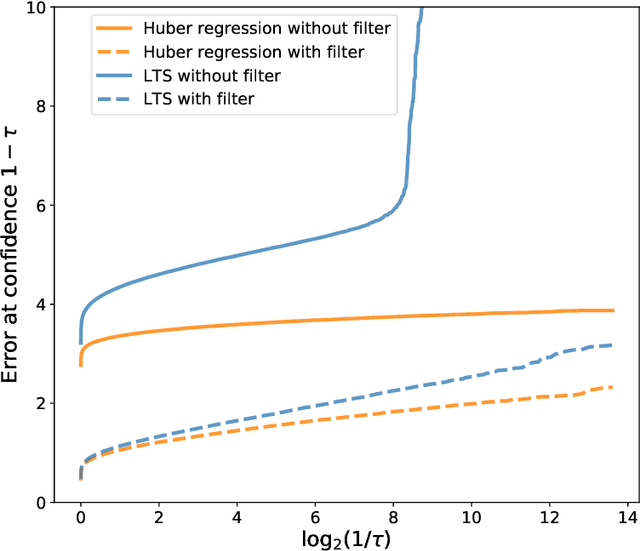
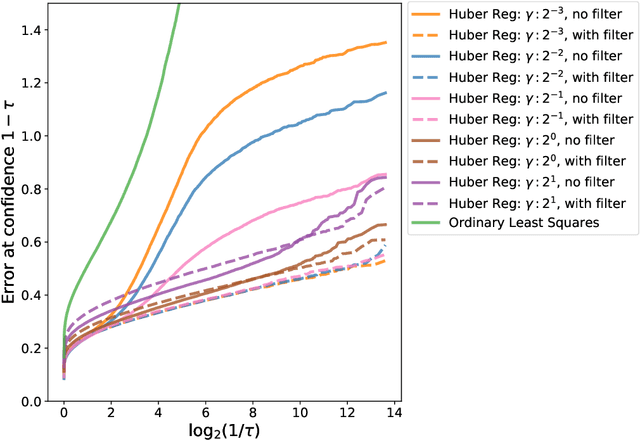
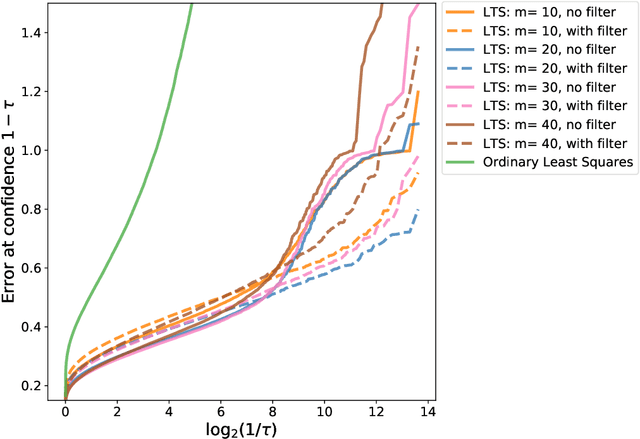
We study the problem of linear regression where both covariates and responses are potentially (i) heavy-tailed and (ii) adversarially contaminated. Several computationally efficient estimators have been proposed for the simpler setting where the covariates are sub-Gaussian and uncontaminated; however, these estimators may fail when the covariates are either heavy-tailed or contain outliers. In this work, we show how to modify the Huber regression, least trimmed squares, and least absolute deviation estimators to obtain estimators which are simultaneously computationally and statistically efficient in the stronger contamination model. Our approach is quite simple, and consists of applying a filtering algorithm to the covariates, and then applying the classical robust regression estimators to the remaining data. We show that the Huber regression estimator achieves near-optimal error rates in this setting, whereas the least trimmed squares and least absolute deviation estimators can be made to achieve near-optimal error after applying a postprocessing step.

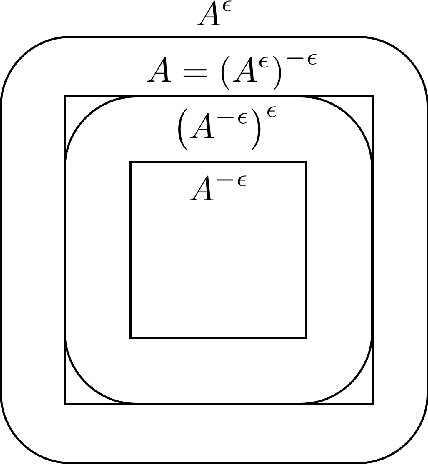
Reverse Lebesgue and Gaussian isoperimetric inequalities for parallel sets with applications

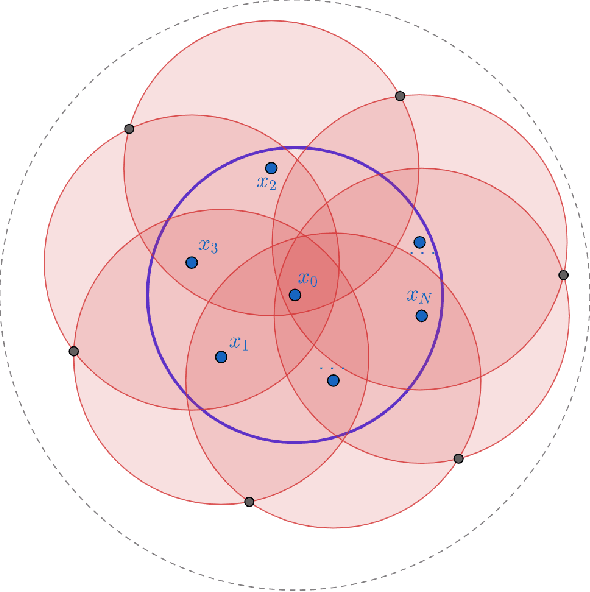
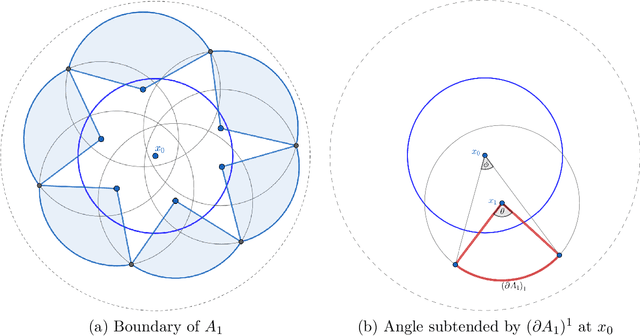
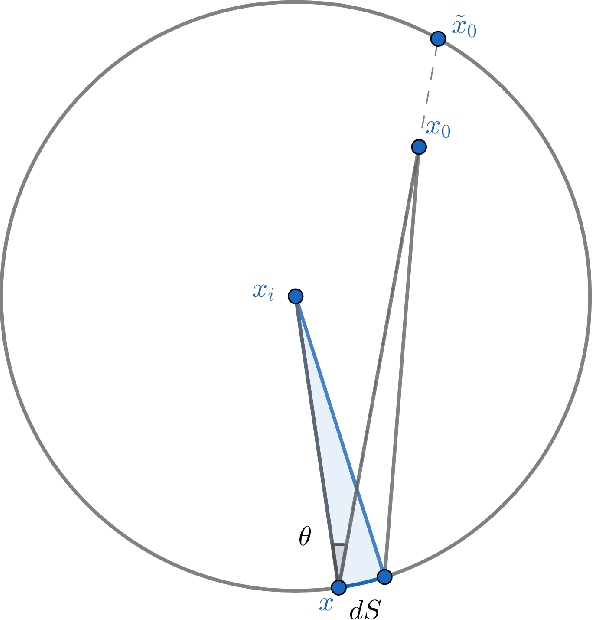
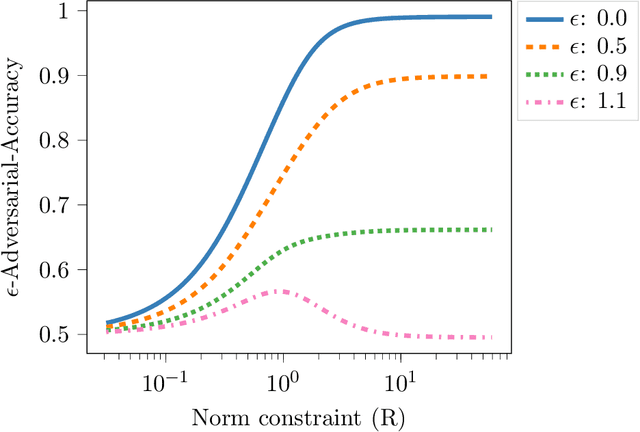
The $r$-parallel set of a measurable set $A \subseteq \mathbb R^d$ is the set of all points whose distance from $A$ is at most $r$. In this paper, we show that the surface area of an $r$-parallel set in $\mathbb R^d$ with volume at most $V$ is upper-bounded by $e^{\Theta(d)}V/r$. We also show that the Gaussian surface area of any $r$-parallel set in $\mathbb R^d$ is upper-bounded by $\max(e^{\Theta(d)}, e^{\Theta(d)}/r)$. We apply our results to two problems in theoretical machine learning: (1) bounding the computational complexity of learning $r$-parallel sets under a Gaussian distribution; and (2) bounding the sample complexity of estimating robust risk, which is a notion of risk in the adversarial machine learning literature that is analogous to the Bayes risk in hypothesis testing.

Adversarial Risk via Optimal Transport and Optimal Couplings

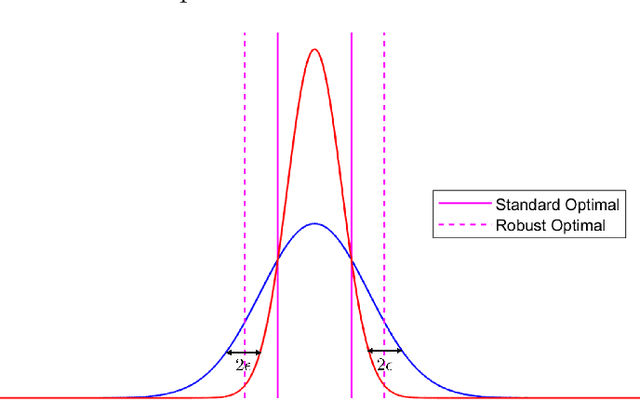
The accuracy of modern machine learning algorithms deteriorates severely on adversarially manipulated test data. Optimal adversarial risk quantifies the best error rate of any classifier in the presence of adversaries, and optimal adversarial classifiers are sought that minimize adversarial risk. In this paper, we investigate the optimal adversarial risk and optimal adversarial classifiers from an optimal transport perspective. We present a new and simple approach to show that the optimal adversarial risk for binary classification with $0-1$ loss function is completely characterized by an optimal transport cost between the probability distributions of the two classes, for a suitably defined cost function. We propose a novel coupling strategy that achieves the optimal transport cost for several univariate distributions like Gaussian, uniform and triangular. Using the optimal couplings, we obtain the optimal adversarial classifiers in these settings and show how they differ from optimal classifiers in the absence of adversaries. Based on our analysis, we evaluate algorithm-independent fundamental limits on adversarial risk for CIFAR-10, MNIST, Fashion-MNIST and SVHN datasets, and Gaussian mixtures based on them. In addition to the $0-1$ loss, we also derive bounds on the deviation of optimal risk and optimal classifier in the presence of adversaries for continuous loss functions, that are based on the convexity and smoothness of the loss functions.

Extracting robust and accurate features via a robust information bottleneck

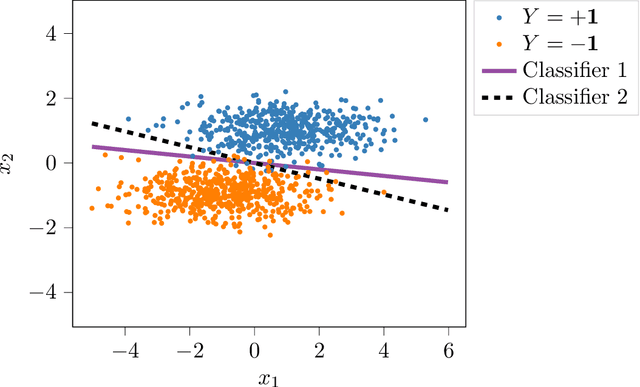
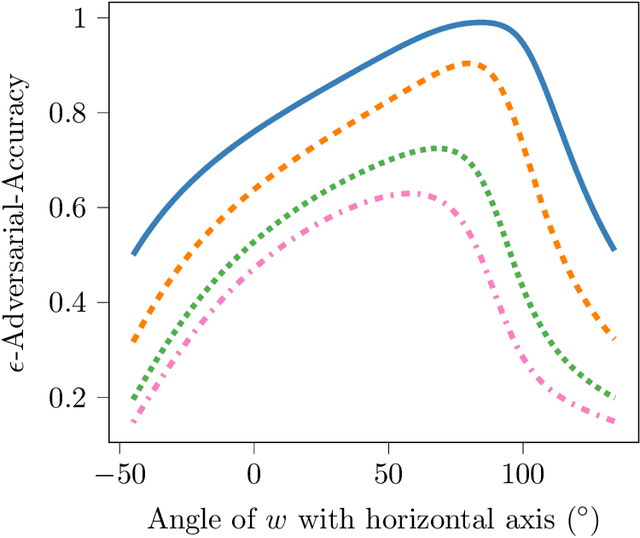
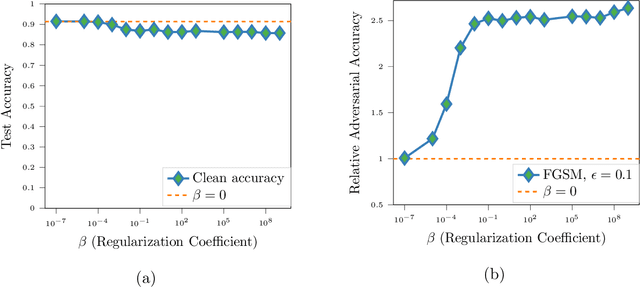
We propose a novel strategy for extracting features in supervised learning that can be used to construct a classifier which is more robust to small perturbations in the input space. Our method builds upon the idea of the information bottleneck by introducing an additional penalty term that encourages the Fisher information of the extracted features to be small, when parametrized by the inputs. By tuning the regularization parameter, we can explicitly trade off the opposing desiderata of robustness and accuracy when constructing a classifier. We derive the optimal solution to the robust information bottleneck when the inputs and outputs are jointly Gaussian, proving that the optimally robust features are also jointly Gaussian in that setting. Furthermore, we propose a method for optimizing a variational bound on the robust information bottleneck objective in general settings using stochastic gradient descent, which may be implemented efficiently in neural networks. Our experimental results for synthetic and real data sets show that the proposed feature extraction method indeed produces classifiers with increased robustness to perturbations.

Robustifying deep networks for image segmentation

Purpose: The purpose of this study is to investigate the robustness of a commonly-used convolutional neural network for image segmentation with respect to visually-subtle adversarial perturbations, and suggest new methods to make these networks more robust to such perturbations. Materials and Methods: In this retrospective study, the accuracy of brain tumor segmentation was studied in subjects with low- and high-grade gliomas. A three-dimensional UNet model was implemented to segment four different MR series (T1-weighted, post-contrast T1-weighted, T2- weighted, and T2-weighted FLAIR) into four pixelwise labels (Gd-enhancing tumor, peritumoral edema, necrotic and non-enhancing tumor, and background). We developed attack strategies based on the Fast Gradient Sign Method (FGSM), iterative FGSM (i-FGSM), and targeted iterative FGSM (ti-FGSM) to produce effective attacks. Additionally, we explored the effectiveness of distillation and adversarial training via data augmentation to counteract adversarial attacks. Robustness was measured by comparing the Dice coefficient for each attack method using Wilcoxon signed-rank tests. Results: Attacks based on FGSM, i-FGSM, and ti-FGSM were effective in significantly reducing the quality of image segmentation with reductions in Dice coefficient by up to 65%. For attack defenses, distillation performed significantly better than adversarial training approaches. However, all defense approaches performed worse compared to unperturbed test images. Conclusion: Segmentation networks can be adversely affected by targeted attacks that introduce visually minor (and potentially undetectable) modifications to existing images. With an increasing interest in applying deep learning techniques to medical imaging data, it is important to quantify the ramifications of adversarial inputs (either intentional or unintentional).

Estimating location parameters in entangled single-sample distributions

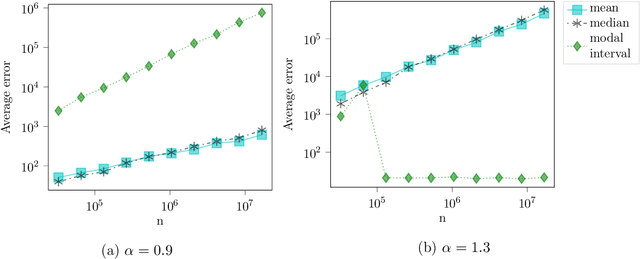
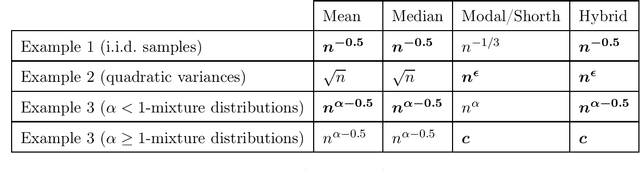
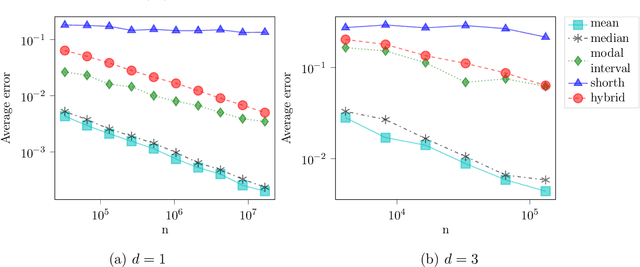
We consider the problem of estimating the common mean of independently sampled data, where samples are drawn in a possibly non-identical manner from symmetric, unimodal distributions with a common mean. This generalizes the setting of Gaussian mixture modeling, since the number of distinct mixture components may diverge with the number of observations. We propose an estimator that adapts to the level of heterogeneity in the data, achieving near-optimality in both the i.i.d. setting and some heterogeneous settings, where the fraction of ``low-noise'' points is as small as $\frac{\log n}{n}$. Our estimator is a hybrid of the modal interval, shorth, and median estimators from classical statistics; however, the key technical contributions rely on novel empirical process theory results that we derive for independent but non-i.i.d. data. In the multivariate setting, we generalize our theory to mean estimation for mixtures of radially symmetric distributions, and derive minimax lower bounds on the expected error of any estimator that is agnostic to the scales of individual data points. Finally, we describe an extension of our estimators applicable to linear regression. In the multivariate mean estimation and regression settings, we present computationally feasible versions of our estimators that run in time polynomial in the number of data points.