Extracting robust and accurate features via a robust information bottleneck
Paper and Code
Oct 15, 2019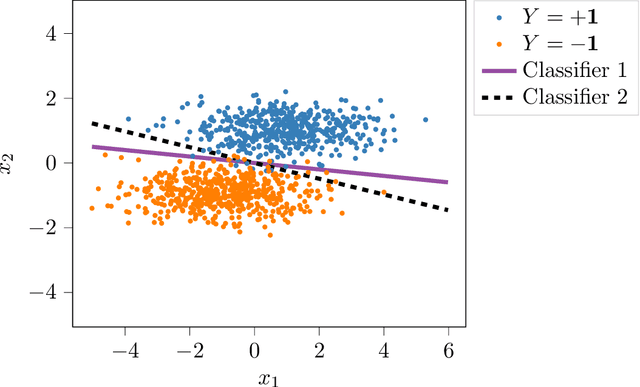
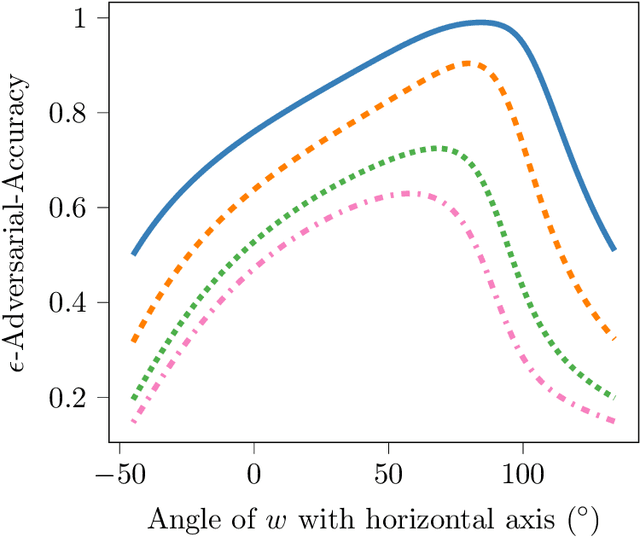
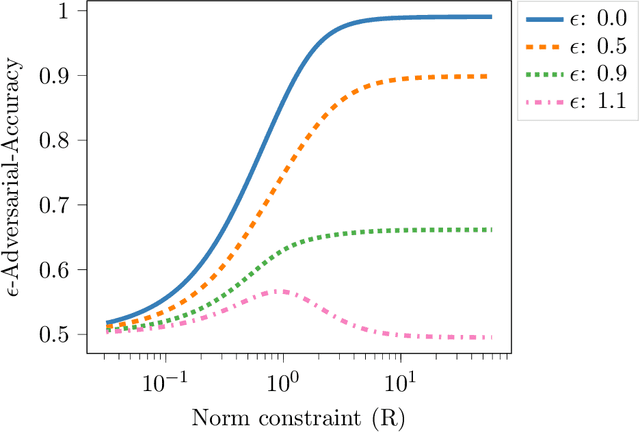
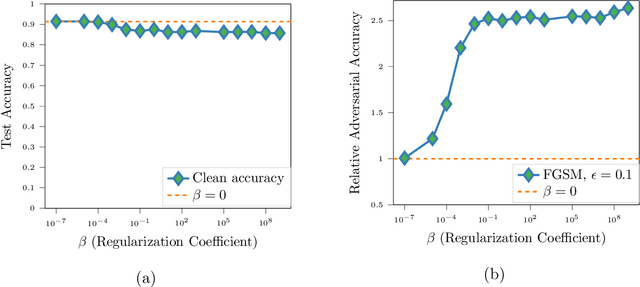
We propose a novel strategy for extracting features in supervised learning that can be used to construct a classifier which is more robust to small perturbations in the input space. Our method builds upon the idea of the information bottleneck by introducing an additional penalty term that encourages the Fisher information of the extracted features to be small, when parametrized by the inputs. By tuning the regularization parameter, we can explicitly trade off the opposing desiderata of robustness and accuracy when constructing a classifier. We derive the optimal solution to the robust information bottleneck when the inputs and outputs are jointly Gaussian, proving that the optimally robust features are also jointly Gaussian in that setting. Furthermore, we propose a method for optimizing a variational bound on the robust information bottleneck objective in general settings using stochastic gradient descent, which may be implemented efficiently in neural networks. Our experimental results for synthetic and real data sets show that the proposed feature extraction method indeed produces classifiers with increased robustness to perturbations.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge