Generalization Error of the Tilted Empirical Risk

The generalization error (risk) of a supervised statistical learning algorithm quantifies its prediction ability on previously unseen data. Inspired by exponential tilting, Li et al. (2021) proposed the tilted empirical risk as a non-linear risk metric for machine learning applications such as classification and regression problems. In this work, we examine the generalization error of the tilted empirical risk. In particular, we provide uniform and information-theoretic bounds on the tilted generalization error, defined as the difference between the population risk and the tilted empirical risk, with a convergence rate of $O(1/\sqrt{n})$ where $n$ is the number of training samples. Furthermore, we study the solution to the KL-regularized expected tilted empirical risk minimization problem and derive an upper bound on the expected tilted generalization error with a convergence rate of $O(1/n)$.

Simple Binary Hypothesis Testing under Local Differential Privacy and Communication Constraints

We study simple binary hypothesis testing under both local differential privacy (LDP) and communication constraints. We qualify our results as either minimax optimal or instance optimal: the former hold for the set of distribution pairs with prescribed Hellinger divergence and total variation distance, whereas the latter hold for specific distribution pairs. For the sample complexity of simple hypothesis testing under pure LDP constraints, we establish instance-optimal bounds for distributions with binary support; minimax-optimal bounds for general distributions; and (approximately) instance-optimal, computationally efficient algorithms for general distributions. When both privacy and communication constraints are present, we develop instance-optimal, computationally efficient algorithms that achieve the minimum possible sample complexity (up to universal constants). Our results on instance-optimal algorithms hinge on identifying the extreme points of the joint range set $\mathcal A$ of two distributions $p$ and $q$, defined as $\mathcal A := \{(\mathbf T p, \mathbf T q) | \mathbf T \in \mathcal C\}$, where $\mathcal C$ is the set of channels characterizing the constraints.

An Entropy-Based Model for Hierarchical Learning

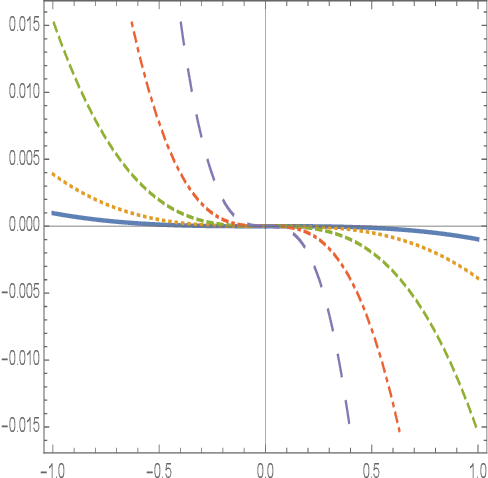
Machine learning is the dominant approach to artificial intelligence, through which computers learn from data and experience. In the framework of supervised learning, for a computer to learn from data accurately and efficiently, some auxiliary information about the data distribution and target function should be provided to it through the learning model. This notion of auxiliary information relates to the concept of regularization in statistical learning theory. A common feature among real-world datasets is that data domains are multiscale and target functions are well-behaved and smooth. In this paper, we propose a learning model that exploits this multiscale data structure and discuss its statistical and computational benefits. The hierarchical learning model is inspired by the logical and progressive easy-to-hard learning mechanism of human beings and has interpretable levels. The model apportions computational resources according to the complexity of data instances and target functions. This property can have multiple benefits, including higher inference speed and computational savings in training a model for many users or when training is interrupted. We provide a statistical analysis of the learning mechanism using multiscale entropies and show that it can yield significantly stronger guarantees than uniform convergence bounds.

Maximum Multiscale Entropy and Neural Network Regularization

A well-known result across information theory, machine learning, and statistical physics shows that the maximum entropy distribution under a mean constraint has an exponential form called the Gibbs-Boltzmann distribution. This is used for instance in density estimation or to achieve excess risk bounds derived from single-scale entropy regularizers (Xu-Raginsky '17). This paper investigates a generalization of these results to a multiscale setting. We present different ways of generalizing the maximum entropy result by incorporating the notion of scale. For different entropies and arbitrary scale transformations, it is shown that the distribution maximizing a multiscale entropy is characterized by a procedure which has an analogy to the renormalization group procedure in statistical physics. For the case of decimation transformation, it is further shown that this distribution is Gaussian whenever the optimal single-scale distribution is Gaussian. This is then applied to neural networks, and it is shown that in a teacher-student scenario, the multiscale Gibbs posterior can achieve a smaller excess risk than the single-scale Gibbs posterior.

Chaining Meets Chain Rule: Multilevel Entropic Regularization and Training of Neural Nets

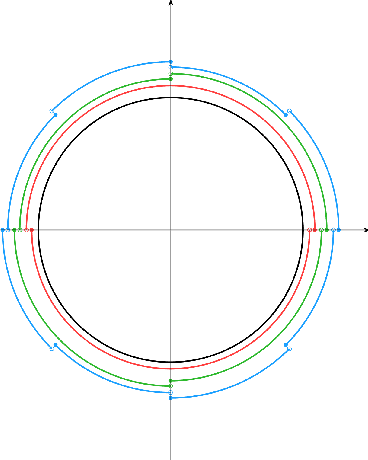
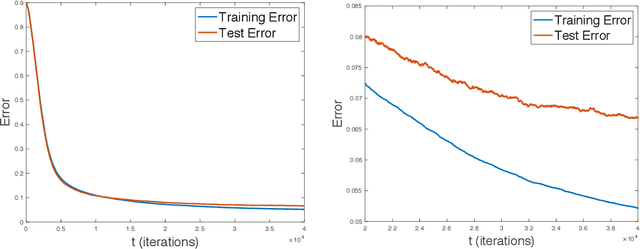
We derive generalization and excess risk bounds for neural nets using a family of complexity measures based on a multilevel relative entropy. The bounds are obtained by introducing the notion of generated hierarchical coverings of neural nets and by using the technique of chaining mutual information introduced in Asadi et al. NeurIPS'18. The resulting bounds are algorithm-dependent and exploit the multilevel structure of neural nets. This, in turn, leads to an empirical risk minimization problem with a multilevel entropic regularization. The minimization problem is resolved by introducing a multi-scale generalization of the celebrated Gibbs posterior distribution, proving that the derived distribution achieves the unique minimum. This leads to a new training procedure for neural nets with performance guarantees, which exploits the chain rule of relative entropy rather than the chain rule of derivatives (as in backpropagation). To obtain an efficient implementation of the latter, we further develop a multilevel Metropolis algorithm simulating the multi-scale Gibbs distribution, with an experiment for a two-layer neural net on the MNIST data set.

Chaining Mutual Information and Tightening Generalization Bounds

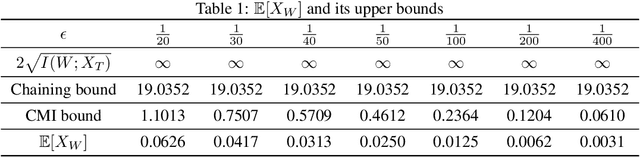
Bounding the generalization error of learning algorithms has a long history, that yet falls short in explaining various generalization successes including those of deep learning. Two important difficulties are (i) exploiting the dependencies between the hypotheses, (ii) exploiting the dependence between the algorithm's input and output. Progress on the first point was made with the chaining method, originating from the work of Kolmogorov and used in the VC-dimension bound. More recently, progress on the second point was made with the mutual information method by Russo and Zou '15. Yet, these two methods are currently disjoint. In this paper, we introduce a technique to combine chaining and mutual information methods, to obtain a generalization bound that is both algorithm-dependent and that exploits the dependencies between the hypotheses. We provide an example in which our bound significantly outperforms both the chaining and the mutual information bounds. As a corollary, we tighten Dudley inequality under the knowledge that a learning algorithm chooses its output from a small subset of hypotheses with high probability; an assumption motivated by the performance of SGD discussed in Zhang et al. '17.