Sergio Verdú
Chaining Mutual Information and Tightening Generalization Bounds
Jun 11, 2018
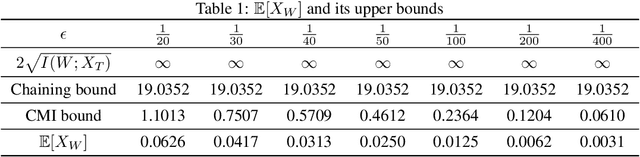
Abstract:Bounding the generalization error of learning algorithms has a long history, that yet falls short in explaining various generalization successes including those of deep learning. Two important difficulties are (i) exploiting the dependencies between the hypotheses, (ii) exploiting the dependence between the algorithm's input and output. Progress on the first point was made with the chaining method, originating from the work of Kolmogorov and used in the VC-dimension bound. More recently, progress on the second point was made with the mutual information method by Russo and Zou '15. Yet, these two methods are currently disjoint. In this paper, we introduce a technique to combine chaining and mutual information methods, to obtain a generalization bound that is both algorithm-dependent and that exploits the dependencies between the hypotheses. We provide an example in which our bound significantly outperforms both the chaining and the mutual information bounds. As a corollary, we tighten Dudley inequality under the knowledge that a learning algorithm chooses its output from a small subset of hypotheses with high probability; an assumption motivated by the performance of SGD discussed in Zhang et al. '17.
$f$-Divergence Inequalities via Functional Domination
Oct 28, 2016Abstract:This paper considers derivation of $f$-divergence inequalities via the approach of functional domination. Bounds on an $f$-divergence based on one or several other $f$-divergences are introduced, dealing with pairs of probability measures defined on arbitrary alphabets. In addition, a variety of bounds are shown to hold under boundedness assumptions on the relative information. The journal paper, which includes more approaches for the derivation of f-divergence inequalities and proofs, is available on the arXiv at https://arxiv.org/abs/1508.00335, and it has been published in the IEEE Trans. on Information Theory, vol. 62, no. 11, pp. 5973-6006, November 2016.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge