Algorithm Discovery With LLMs: Evolutionary Search Meets Reinforcement Learning

Discovering efficient algorithms for solving complex problems has been an outstanding challenge in mathematics and computer science, requiring substantial human expertise over the years. Recent advancements in evolutionary search with large language models (LLMs) have shown promise in accelerating the discovery of algorithms across various domains, particularly in mathematics and optimization. However, existing approaches treat the LLM as a static generator, missing the opportunity to update the model with the signal obtained from evolutionary exploration. In this work, we propose to augment LLM-based evolutionary search by continuously refining the search operator - the LLM - through reinforcement learning (RL) fine-tuning. Our method leverages evolutionary search as an exploration strategy to discover improved algorithms, while RL optimizes the LLM policy based on these discoveries. Our experiments on three combinatorial optimization tasks - bin packing, traveling salesman, and the flatpack problem - show that combining RL and evolutionary search improves discovery efficiency of improved algorithms, showcasing the potential of RL-enhanced evolutionary strategies to assist computer scientists and mathematicians for more efficient algorithm design.

Reversal Blessing: Thinking Backward May Outpace Thinking Forward in Multi-choice Questions

Language models usually use left-to-right (L2R) autoregressive factorization. However, L2R factorization may not always be the best inductive bias. Therefore, we investigate whether alternative factorizations of the text distribution could be beneficial in some tasks. We investigate right-to-left (R2L) training as a compelling alternative, focusing on multiple-choice questions (MCQs) as a test bed for knowledge extraction and reasoning. Through extensive experiments across various model sizes (2B-8B parameters) and training datasets, we find that R2L models can significantly outperform L2R models on several MCQ benchmarks, including logical reasoning, commonsense understanding, and truthfulness assessment tasks. Our analysis reveals that this performance difference may be fundamentally linked to multiple factors including calibration, computability and directional conditional entropy. We ablate the impact of these factors through controlled simulation studies using arithmetic tasks, where the impacting factors can be better disentangled. Our work demonstrates that exploring alternative factorizations of the text distribution can lead to improvements in LLM capabilities and provides theoretical insights into optimal factorization towards approximating human language distribution, and when each reasoning order might be more advantageous.

Learning High-Degree Parities: The Crucial Role of the Initialization

Parities have become a standard benchmark for evaluating learning algorithms. Recent works show that regular neural networks trained by gradient descent can efficiently learn degree $k$ parities on uniform inputs for constant $k$, but fail to do so when $k$ and $d-k$ grow with $d$ (here $d$ is the ambient dimension). However, the case where $k=d-O_d(1)$ (almost-full parities), including the degree $d$ parity (the full parity), has remained unsettled. This paper shows that for gradient descent on regular neural networks, learnability depends on the initial weight distribution. On one hand, the discrete Rademacher initialization enables efficient learning of almost-full parities, while on the other hand, its Gaussian perturbation with large enough constant standard deviation $\sigma$ prevents it. The positive result for almost-full parities is shown to hold up to $\sigma=O(d^{-1})$, pointing to questions about a sharper threshold phenomenon. Unlike statistical query (SQ) learning, where a singleton function class like the full parity is trivially learnable, our negative result applies to a fixed function and relies on an initial gradient alignment measure of potential broader relevance to neural networks learning.

Transformation-Invariant Learning and Theoretical Guarantees for OOD Generalization

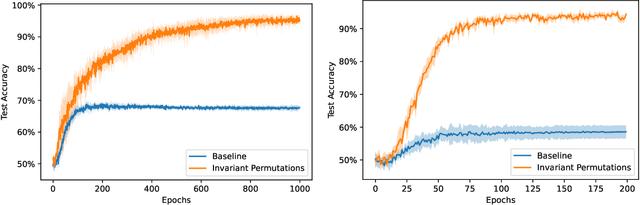
Learning with identical train and test distributions has been extensively investigated both practically and theoretically. Much remains to be understood, however, in statistical learning under distribution shifts. This paper focuses on a distribution shift setting where train and test distributions can be related by classes of (data) transformation maps. We initiate a theoretical study for this framework, investigating learning scenarios where the target class of transformations is either known or unknown. We establish learning rules and algorithmic reductions to Empirical Risk Minimization (ERM), accompanied with learning guarantees. We obtain upper bounds on the sample complexity in terms of the VC dimension of the class composing predictors with transformations, which we show in many cases is not much larger than the VC dimension of the class of predictors. We highlight that the learning rules we derive offer a game-theoretic viewpoint on distribution shift: a learner searching for predictors and an adversary searching for transformation maps to respectively minimize and maximize the worst-case loss.

Visual Scratchpads: Enabling Global Reasoning in Vision

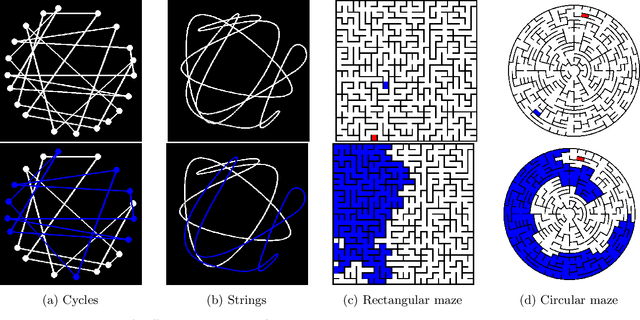
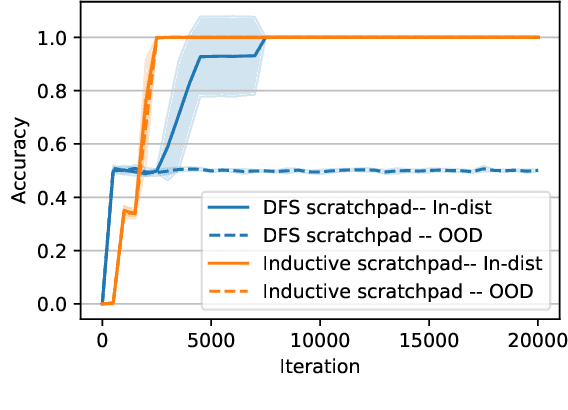
Modern vision models have achieved remarkable success in benchmarks where local features provide critical information about the target. There is now a growing interest in solving tasks that require more global reasoning, where local features offer no significant information. These tasks are reminiscent of the connectivity tasks discussed by Minsky and Papert in 1969, which exposed the limitations of the perceptron model and contributed to the first AI winter. In this paper, we revisit such tasks by introducing four global visual benchmarks involving path findings and mazes. We show that: (1) although today's large vision models largely surpass the expressivity limitations of the early models, they still struggle with the learning efficiency; we put forward the "globality degree" notion to understand this limitation; (2) we then demonstrate that the picture changes and global reasoning becomes feasible with the introduction of "visual scratchpads"; similarly to the text scratchpads and chain-of-thoughts used in language models, visual scratchpads help break down global tasks into simpler ones; (3) we finally show that some scratchpads are better than others, in particular, "inductive scratchpads" that take steps relying on less information afford better out-of-distribution generalization and succeed for smaller model sizes.

On the Minimal Degree Bias in Generalization on the Unseen for non-Boolean Functions

We investigate the out-of-domain generalization of random feature (RF) models and Transformers. We first prove that in the `generalization on the unseen (GOTU)' setting, where training data is fully seen in some part of the domain but testing is made on another part, and for RF models in the small feature regime, the convergence takes place to interpolators of minimal degree as in the Boolean case (Abbe et al., 2023). We then consider the sparse target regime and explain how this regime relates to the small feature regime, but with a different regularization term that can alter the picture in the non-Boolean case. We show two different outcomes for the sparse regime with q-ary data tokens: (1) if the data is embedded with roots of unities, then a min-degree interpolator is learned like in the Boolean case for RF models, (2) if the data is not embedded as such, e.g., simply as integers, then RF models and Transformers may not learn minimal degree interpolators. This shows that the Boolean setting and its roots of unities generalization are special cases where the minimal degree interpolator offers a rare characterization of how learning takes place. For more general integer and real-valued settings, a more nuanced picture remains to be fully characterized.

How Far Can Transformers Reason? The Locality Barrier and Inductive Scratchpad

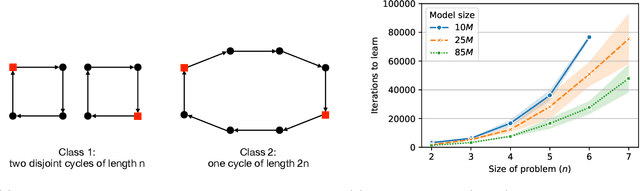
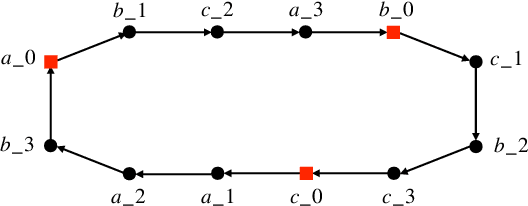
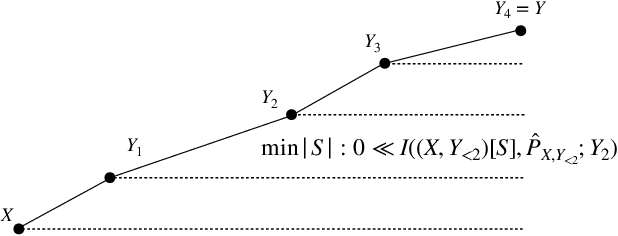
Can Transformers predict new syllogisms by composing established ones? More generally, what type of targets can be learned by such models from scratch? Recent works show that Transformers can be Turing-complete in terms of expressivity, but this does not address the learnability objective. This paper puts forward the notion of 'distribution locality' to capture when weak learning is efficiently achievable by regular Transformers, where the locality measures the least number of tokens required in addition to the tokens histogram to correlate nontrivially with the target. As shown experimentally and theoretically under additional assumptions, distributions with high locality cannot be learned efficiently. In particular, syllogisms cannot be composed on long chains. Furthermore, we show that (i) an agnostic scratchpad cannot help to break the locality barrier, (ii) an educated scratchpad can help if it breaks the locality at each step, (iii) a notion of 'inductive scratchpad' can both break the locality and improve the out-of-distribution generalization, e.g., generalizing to almost double input size for some arithmetic tasks.

When can transformers reason with abstract symbols?

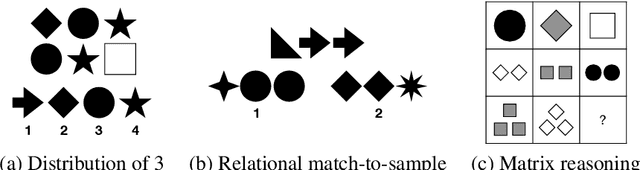
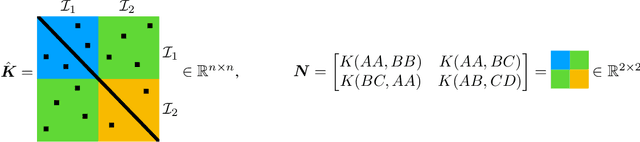
We investigate the capabilities of transformer large language models (LLMs) on relational reasoning tasks involving abstract symbols. Such tasks have long been studied in the neuroscience literature as fundamental building blocks for more complex abilities in programming, mathematics, and verbal reasoning. For (i) regression tasks, we prove that transformers generalize when trained, but require astonishingly large quantities of training data. For (ii) next-token-prediction tasks with symbolic labels, we show an "inverse scaling law": transformers fail to generalize as their embedding dimension increases. For both settings (i) and (ii), we propose subtle transformer modifications which can reduce the amount of data needed by adding two trainable parameters per head.

Provable Advantage of Curriculum Learning on Parity Targets with Mixed Inputs

Experimental results have shown that curriculum learning, i.e., presenting simpler examples before more complex ones, can improve the efficiency of learning. Some recent theoretical results also showed that changing the sampling distribution can help neural networks learn parities, with formal results only for large learning rates and one-step arguments. Here we show a separation result in the number of training steps with standard (bounded) learning rates on a common sample distribution: if the data distribution is a mixture of sparse and dense inputs, there exists a regime in which a 2-layer ReLU neural network trained by a curriculum noisy-GD (or SGD) algorithm that uses sparse examples first, can learn parities of sufficiently large degree, while any fully connected neural network of possibly larger width or depth trained by noisy-GD on the unordered samples cannot learn without additional steps. We also provide experimental results supporting the qualitative separation beyond the specific regime of the theoretical results.

Transformers learn through gradual rank increase

We identify incremental learning dynamics in transformers, where the difference between trained and initial weights progressively increases in rank. We rigorously prove this occurs under the simplifying assumptions of diagonal weight matrices and small initialization. Our experiments support the theory and also show that phenomenon can occur in practice without the simplifying assumptions.