AbstRaL: Augmenting LLMs' Reasoning by Reinforcing Abstract Thinking

Recent studies have shown that large language models (LLMs), especially smaller ones, often lack robustness in their reasoning. I.e., they tend to experience performance drops when faced with distribution shifts, such as changes to numerical or nominal variables, or insertions of distracting clauses. A possible strategy to address this involves generating synthetic data to further "instantiate" reasoning problems on potential variations. In contrast, our approach focuses on "abstracting" reasoning problems. This not only helps counteract distribution shifts but also facilitates the connection to symbolic tools for deriving solutions. We find that this abstraction process is better acquired through reinforcement learning (RL) than just supervised fine-tuning, which often fails to produce faithful abstractions. Our method, AbstRaL -- which promotes abstract reasoning in LLMs using RL on granular abstraction data -- significantly mitigates performance degradation on recent GSM perturbation benchmarks.

Augmenting LLMs' Reasoning by Reinforcing Abstract Thinking

Recent studies have shown that large language models (LLMs), especially smaller ones, often lack robustness in their reasoning. I.e., they tend to experience performance drops when faced with distribution shifts, such as changes to numerical or nominal variables, or insertions of distracting clauses. A possible strategy to address this involves generating synthetic data to further "instantiate" reasoning problems on potential variations. In contrast, our approach focuses on "abstracting" reasoning problems. This not only helps counteract distribution shifts but also facilitates the connection to symbolic tools for deriving solutions. We find that this abstraction process is better acquired through reinforcement learning (RL) than just supervised fine-tuning, which often fails to produce faithful abstractions. Our method, AbstraL -- which promotes abstract reasoning in LLMs using RL on granular abstraction data -- significantly mitigates performance degradation on recent GSM perturbation benchmarks.

The Illusion of Thinking: Understanding the Strengths and Limitations of Reasoning Models via the Lens of Problem Complexity

Recent generations of language models have introduced Large Reasoning Models (LRMs) that generate detailed thinking processes before providing answers. While these models demonstrate improved performance on reasoning benchmarks, their fundamental capabilities, scaling properties, and limitations remain insufficiently understood. Current evaluations primarily focus on established math and coding benchmarks, emphasizing final answer accuracy. However, this evaluation paradigm often suffers from contamination and does not provide insights into the reasoning traces. In this work, we systematically investigate these gaps with the help of controllable puzzle environments that allow precise manipulation of complexity while maintaining consistent logical structures. This setup enables the analysis of not only final answers but also the internal reasoning traces, offering insights into how LRMs think. Through extensive experiments, we show that LRMs face a complete accuracy collapse beyond certain complexities. Moreover, they exhibit a counterintuitive scaling limit: their reasoning effort increases with problem complexity up to a point, then declines despite having remaining token budget. By comparing LRMs with their standard LLM counterparts under same inference compute, we identify three performance regimes: (1) low-complexity tasks where standard models outperform LRMs, (2) medium-complexity tasks where LRMs demonstrates advantage, and (3) high-complexity tasks where both models face complete collapse. We found that LRMs have limitations in exact computation: they fail to use explicit algorithms and reason inconsistently across scales. We also investigate the reasoning traces in more depth, studying the patterns of explored solutions and analyzing the models' computational behavior, shedding light on their strengths, limitations, and raising questions about their reasoning capabilities.

TiC-LM: A Web-Scale Benchmark for Time-Continual LLM Pretraining

Large Language Models (LLMs) trained on historical web data inevitably become outdated. We investigate evaluation strategies and update methods for LLMs as new data becomes available. We introduce a web-scale dataset for time-continual pretraining of LLMs derived from 114 dumps of Common Crawl (CC) - orders of magnitude larger than previous continual language modeling benchmarks. We also design time-stratified evaluations across both general CC data and specific domains (Wikipedia, StackExchange, and code documentation) to assess how well various continual learning methods adapt to new data while retaining past knowledge. Our findings demonstrate that, on general CC data, autoregressive meta-schedules combined with a fixed-ratio replay of older data can achieve comparable held-out loss to re-training from scratch, while requiring significantly less computation (2.6x). However, the optimal balance between incorporating new data and replaying old data differs as replay is crucial to avoid forgetting on generic web data but less so on specific domains.

Reversal Blessing: Thinking Backward May Outpace Thinking Forward in Multi-choice Questions

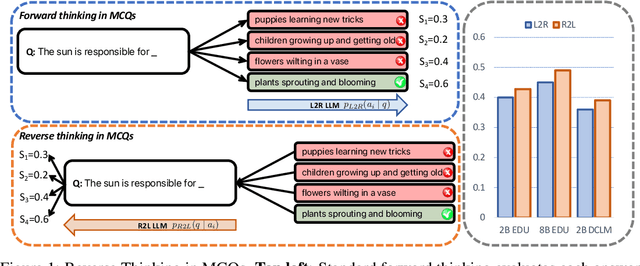
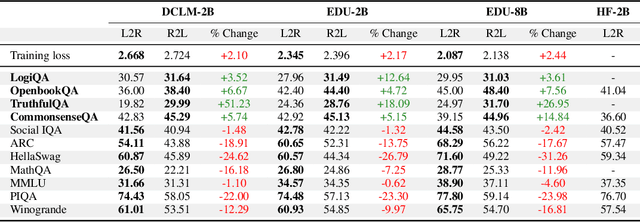
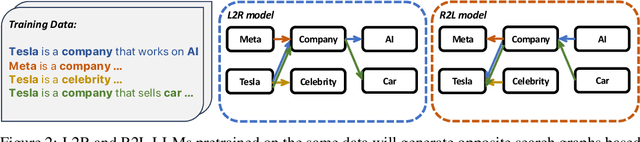
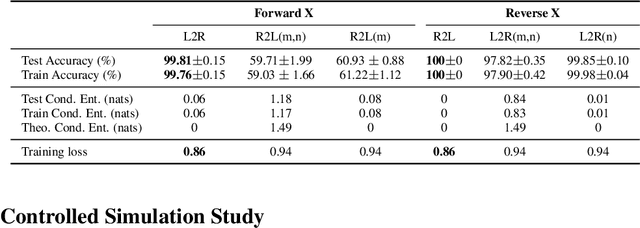
Language models usually use left-to-right (L2R) autoregressive factorization. However, L2R factorization may not always be the best inductive bias. Therefore, we investigate whether alternative factorizations of the text distribution could be beneficial in some tasks. We investigate right-to-left (R2L) training as a compelling alternative, focusing on multiple-choice questions (MCQs) as a test bed for knowledge extraction and reasoning. Through extensive experiments across various model sizes (2B-8B parameters) and training datasets, we find that R2L models can significantly outperform L2R models on several MCQ benchmarks, including logical reasoning, commonsense understanding, and truthfulness assessment tasks. Our analysis reveals that this performance difference may be fundamentally linked to multiple factors including calibration, computability and directional conditional entropy. We ablate the impact of these factors through controlled simulation studies using arithmetic tasks, where the impacting factors can be better disentangled. Our work demonstrates that exploring alternative factorizations of the text distribution can lead to improvements in LLM capabilities and provides theoretical insights into optimal factorization towards approximating human language distribution, and when each reasoning order might be more advantageous.

Visual Scratchpads: Enabling Global Reasoning in Vision

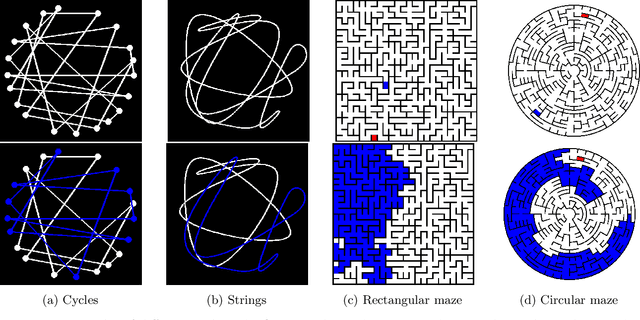
Modern vision models have achieved remarkable success in benchmarks where local features provide critical information about the target. There is now a growing interest in solving tasks that require more global reasoning, where local features offer no significant information. These tasks are reminiscent of the connectivity tasks discussed by Minsky and Papert in 1969, which exposed the limitations of the perceptron model and contributed to the first AI winter. In this paper, we revisit such tasks by introducing four global visual benchmarks involving path findings and mazes. We show that: (1) although today's large vision models largely surpass the expressivity limitations of the early models, they still struggle with the learning efficiency; we put forward the "globality degree" notion to understand this limitation; (2) we then demonstrate that the picture changes and global reasoning becomes feasible with the introduction of "visual scratchpads"; similarly to the text scratchpads and chain-of-thoughts used in language models, visual scratchpads help break down global tasks into simpler ones; (3) we finally show that some scratchpads are better than others, in particular, "inductive scratchpads" that take steps relying on less information afford better out-of-distribution generalization and succeed for smaller model sizes.

GSM-Symbolic: Understanding the Limitations of Mathematical Reasoning in Large Language Models

Recent advancements in Large Language Models (LLMs) have sparked interest in their formal reasoning capabilities, particularly in mathematics. The GSM8K benchmark is widely used to assess the mathematical reasoning of models on grade-school-level questions. While the performance of LLMs on GSM8K has significantly improved in recent years, it remains unclear whether their mathematical reasoning capabilities have genuinely advanced, raising questions about the reliability of the reported metrics. To address these concerns, we conduct a large-scale study on several SOTA open and closed models. To overcome the limitations of existing evaluations, we introduce GSM-Symbolic, an improved benchmark created from symbolic templates that allow for the generation of a diverse set of questions. GSM-Symbolic enables more controllable evaluations, providing key insights and more reliable metrics for measuring the reasoning capabilities of models.Our findings reveal that LLMs exhibit noticeable variance when responding to different instantiations of the same question. Specifically, the performance of all models declines when only the numerical values in the question are altered in the GSM-Symbolic benchmark. Furthermore, we investigate the fragility of mathematical reasoning in these models and show that their performance significantly deteriorates as the number of clauses in a question increases. We hypothesize that this decline is because current LLMs cannot perform genuine logical reasoning; they replicate reasoning steps from their training data. Adding a single clause that seems relevant to the question causes significant performance drops (up to 65%) across all state-of-the-art models, even though the clause doesn't contribute to the reasoning chain needed for the final answer. Overall, our work offers a more nuanced understanding of LLMs' capabilities and limitations in mathematical reasoning.

How Far Can Transformers Reason? The Locality Barrier and Inductive Scratchpad

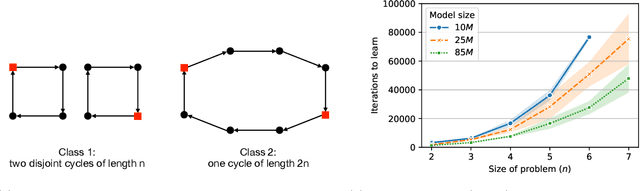
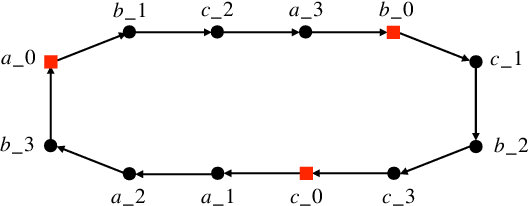
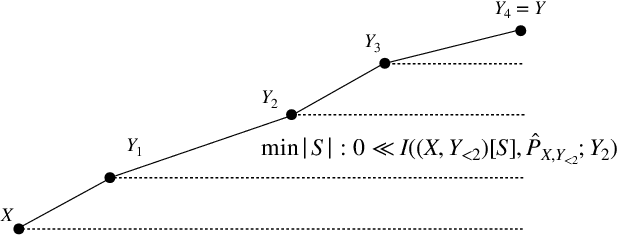
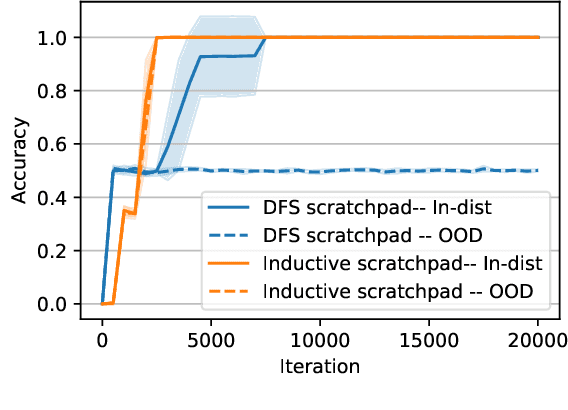
Can Transformers predict new syllogisms by composing established ones? More generally, what type of targets can be learned by such models from scratch? Recent works show that Transformers can be Turing-complete in terms of expressivity, but this does not address the learnability objective. This paper puts forward the notion of 'distribution locality' to capture when weak learning is efficiently achievable by regular Transformers, where the locality measures the least number of tokens required in addition to the tokens histogram to correlate nontrivially with the target. As shown experimentally and theoretically under additional assumptions, distributions with high locality cannot be learned efficiently. In particular, syllogisms cannot be composed on long chains. Furthermore, we show that (i) an agnostic scratchpad cannot help to break the locality barrier, (ii) an educated scratchpad can help if it breaks the locality at each step, (iii) a notion of 'inductive scratchpad' can both break the locality and improve the out-of-distribution generalization, e.g., generalizing to almost double input size for some arithmetic tasks.

What Algorithms can Transformers Learn? A Study in Length Generalization

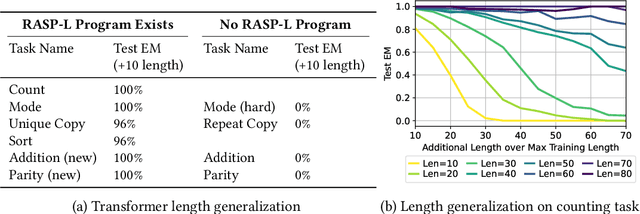
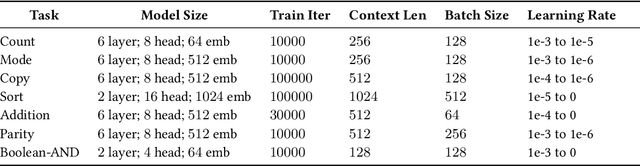
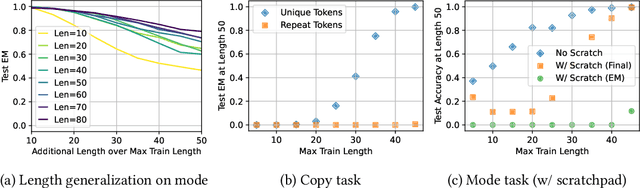
Large language models exhibit surprising emergent generalization properties, yet also struggle on many simple reasoning tasks such as arithmetic and parity. This raises the question of if and when Transformer models can learn the true algorithm for solving a task. We study the scope of Transformers' abilities in the specific setting of length generalization on algorithmic tasks. Here, we propose a unifying framework to understand when and how Transformers can exhibit strong length generalization on a given task. Specifically, we leverage RASP (Weiss et al., 2021) -- a programming language designed for the computational model of a Transformer -- and introduce the RASP-Generalization Conjecture: Transformers tend to length generalize on a task if the task can be solved by a short RASP program which works for all input lengths. This simple conjecture remarkably captures most known instances of length generalization on algorithmic tasks. Moreover, we leverage our insights to drastically improve generalization performance on traditionally hard tasks (such as parity and addition). On the theoretical side, we give a simple example where the "min-degree-interpolator" model of learning from Abbe et al. (2023) does not correctly predict Transformers' out-of-distribution behavior, but our conjecture does. Overall, our work provides a novel perspective on the mechanisms of compositional generalization and the algorithmic capabilities of Transformers.

When can transformers reason with abstract symbols?

We investigate the capabilities of transformer large language models (LLMs) on relational reasoning tasks involving abstract symbols. Such tasks have long been studied in the neuroscience literature as fundamental building blocks for more complex abilities in programming, mathematics, and verbal reasoning. For (i) regression tasks, we prove that transformers generalize when trained, but require astonishingly large quantities of training data. For (ii) next-token-prediction tasks with symbolic labels, we show an "inverse scaling law": transformers fail to generalize as their embedding dimension increases. For both settings (i) and (ii), we propose subtle transformer modifications which can reduce the amount of data needed by adding two trainable parameters per head.