Composition and Control with Distilled Energy Diffusion Models and Sequential Monte Carlo

Diffusion models may be formulated as a time-indexed sequence of energy-based models, where the score corresponds to the negative gradient of an energy function. As opposed to learning the score directly, an energy parameterization is attractive as the energy itself can be used to control generation via Monte Carlo samplers. Architectural constraints and training instability in energy parameterized models have so far yielded inferior performance compared to directly approximating the score or denoiser. We address these deficiencies by introducing a novel training regime for the energy function through distillation of pre-trained diffusion models, resembling a Helmholtz decomposition of the score vector field. We further showcase the synergies between energy and score by casting the diffusion sampling procedure as a Feynman Kac model where sampling is controlled using potentials from the learnt energy functions. The Feynman Kac model formalism enables composition and low temperature sampling through sequential Monte Carlo.

Mechanisms of Projective Composition of Diffusion Models

We study the theoretical foundations of composition in diffusion models, with a particular focus on out-of-distribution extrapolation and length-generalization. Prior work has shown that composing distributions via linear score combination can achieve promising results, including length-generalization in some cases (Du et al., 2023; Liu et al., 2022). However, our theoretical understanding of how and why such compositions work remains incomplete. In fact, it is not even entirely clear what it means for composition to "work". This paper starts to address these fundamental gaps. We begin by precisely defining one possible desired result of composition, which we call projective composition. Then, we investigate: (1) when linear score combinations provably achieve projective composition, (2) whether reverse-diffusion sampling can generate the desired composition, and (3) the conditions under which composition fails. Finally, we connect our theoretical analysis to prior empirical observations where composition has either worked or failed, for reasons that were unclear at the time.

Classifier-Free Guidance is a Predictor-Corrector

We investigate the theoretical foundations of classifier-free guidance (CFG). CFG is the dominant method of conditional sampling for text-to-image diffusion models, yet unlike other aspects of diffusion, it remains on shaky theoretical footing. In this paper, we disprove common misconceptions, by showing that CFG interacts differently with DDPM (Ho et al., 2020) and DDIM (Song et al., 2021), and neither sampler with CFG generates the gamma-powered distribution $p(x|c)^\gamma p(x)^{1-\gamma}$. Then, we clarify the behavior of CFG by showing that it is a kind of predictor-corrector method (Song et al., 2020) that alternates between denoising and sharpening, which we call predictor-corrector guidance (PCG). We prove that in the SDE limit, CFG is actually equivalent to combining a DDIM predictor for the conditional distribution together with a Langevin dynamics corrector for a gamma-powered distribution (with a carefully chosen gamma). Our work thus provides a lens to theoretically understand CFG by embedding it in a broader design space of principled sampling methods.

Step-by-Step Diffusion: An Elementary Tutorial

We present an accessible first course on diffusion models and flow matching for machine learning, aimed at a technical audience with no diffusion experience. We try to simplify the mathematical details as much as possible (sometimes heuristically), while retaining enough precision to derive correct algorithms.

Vanishing Gradients in Reinforcement Finetuning of Language Models

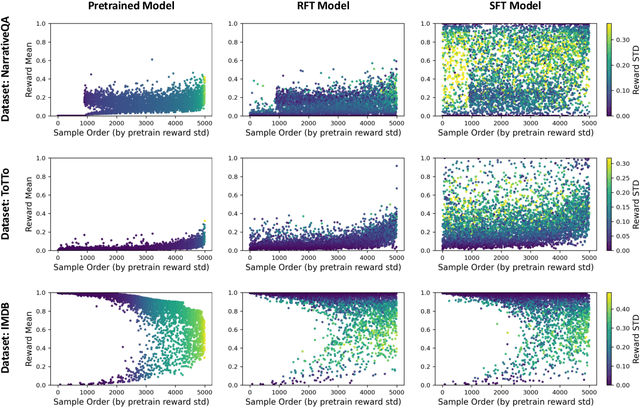
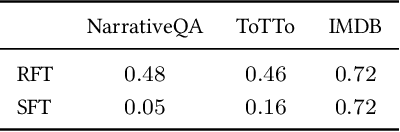
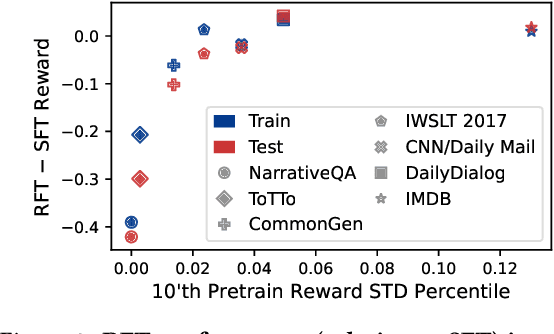
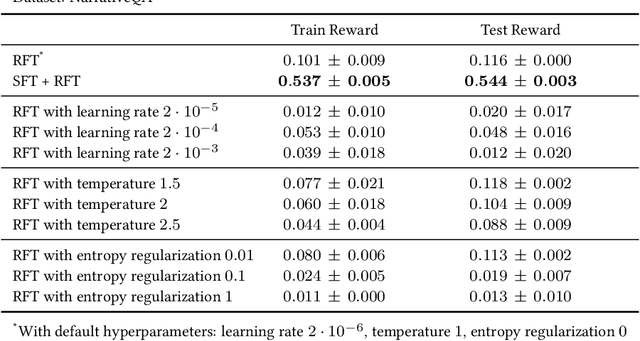
Pretrained language models are commonly aligned with human preferences and downstream tasks via reinforcement finetuning (RFT), which entails maximizing a (possibly learned) reward function using policy gradient algorithms. This work highlights a fundamental optimization obstacle in RFT: we prove that the expected gradient for an input vanishes when its reward standard deviation under the model is small, even if the expected reward is far from optimal. Through experiments on an RFT benchmark and controlled environments, as well as a theoretical analysis, we then demonstrate that vanishing gradients due to small reward standard deviation are prevalent and detrimental, leading to extremely slow reward maximization. Lastly, we explore ways to overcome vanishing gradients in RFT. We find the common practice of an initial supervised finetuning (SFT) phase to be the most promising candidate, which sheds light on its importance in an RFT pipeline. Moreover, we show that a relatively small number of SFT optimization steps on as few as 1% of the input samples can suffice, indicating that the initial SFT phase need not be expensive in terms of compute and data labeling efforts. Overall, our results emphasize that being mindful for inputs whose expected gradient vanishes, as measured by the reward standard deviation, is crucial for successful execution of RFT.

What Algorithms can Transformers Learn? A Study in Length Generalization

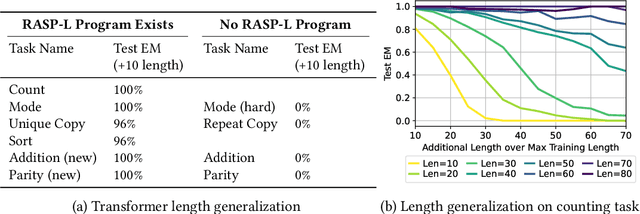
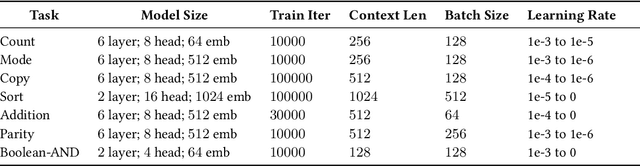
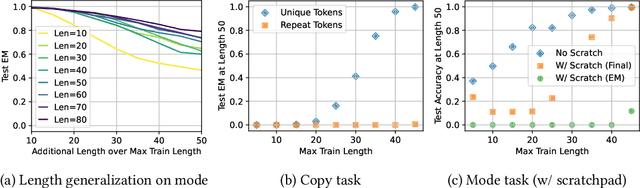
Large language models exhibit surprising emergent generalization properties, yet also struggle on many simple reasoning tasks such as arithmetic and parity. This raises the question of if and when Transformer models can learn the true algorithm for solving a task. We study the scope of Transformers' abilities in the specific setting of length generalization on algorithmic tasks. Here, we propose a unifying framework to understand when and how Transformers can exhibit strong length generalization on a given task. Specifically, we leverage RASP (Weiss et al., 2021) -- a programming language designed for the computational model of a Transformer -- and introduce the RASP-Generalization Conjecture: Transformers tend to length generalize on a task if the task can be solved by a short RASP program which works for all input lengths. This simple conjecture remarkably captures most known instances of length generalization on algorithmic tasks. Moreover, we leverage our insights to drastically improve generalization performance on traditionally hard tasks (such as parity and addition). On the theoretical side, we give a simple example where the "min-degree-interpolator" model of learning from Abbe et al. (2023) does not correctly predict Transformers' out-of-distribution behavior, but our conjecture does. Overall, our work provides a novel perspective on the mechanisms of compositional generalization and the algorithmic capabilities of Transformers.

Cinematic-L1 Video Stabilization with a Log-Homography Model

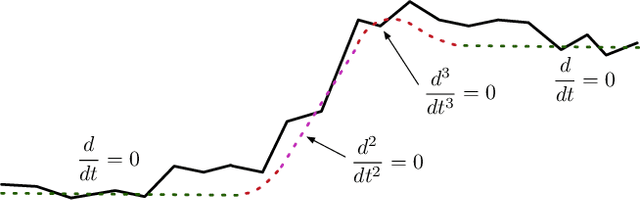
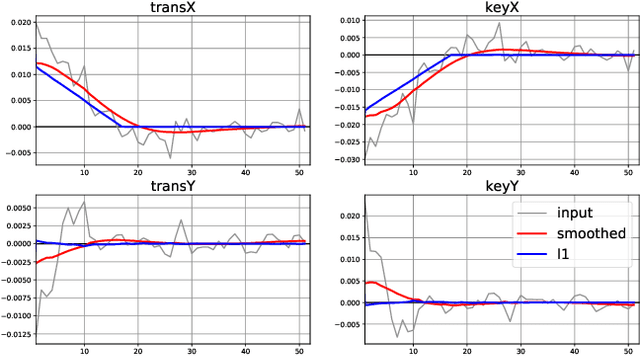
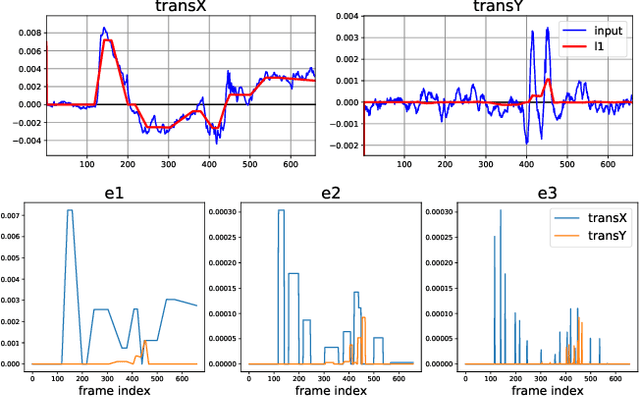
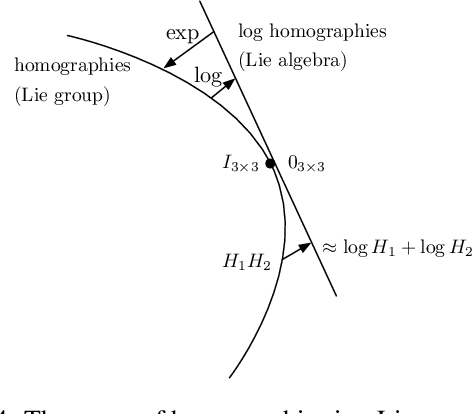
We present a method for stabilizing handheld video that simulates the camera motions cinematographers achieve with equipment like tripods, dollies, and Steadicams. We formulate a constrained convex optimization problem minimizing the $\ell_1$-norm of the first three derivatives of the stabilized motion. Our approach extends the work of Grundmann et al. [9] by solving with full homographies (rather than affinities) in order to correct perspective, preserving linearity by working in log-homography space. We also construct crop constraints that preserve field-of-view; model the problem as a quadratic (rather than linear) program to allow for an $\ell_2$ term encouraging fidelity to the original trajectory; and add constraints and objectives to reduce distortion. Furthermore, we propose new methods for handling salient objects via both inclusion constraints and centering objectives. Finally, we describe a windowing strategy to approximate the solution in linear time and bounded memory. Our method is computationally efficient, running at 300fps on an iPhone XS, and yields high-quality results, as we demonstrate with a collection of stabilized videos, quantitative and qualitative comparisons to [9] and other methods, and an ablation study.