A Formal Framework for Understanding Length Generalization in Transformers

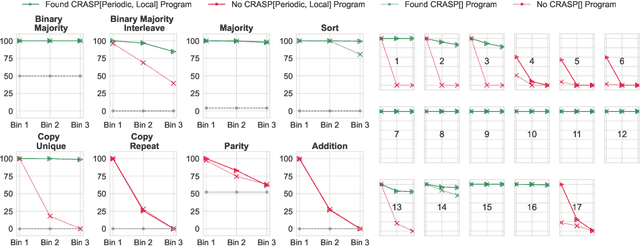
A major challenge for transformers is generalizing to sequences longer than those observed during training. While previous works have empirically shown that transformers can either succeed or fail at length generalization depending on the task, theoretical understanding of this phenomenon remains limited. In this work, we introduce a rigorous theoretical framework to analyze length generalization in causal transformers with learnable absolute positional encodings. In particular, we characterize those functions that are identifiable in the limit from sufficiently long inputs with absolute positional encodings under an idealized inference scheme using a norm-based regularizer. This enables us to prove the possibility of length generalization for a rich family of problems. We experimentally validate the theory as a predictor of success and failure of length generalization across a range of algorithmic and formal language tasks. Our theory not only explains a broad set of empirical observations but also opens the way to provably predicting length generalization capabilities in transformers.

Step-by-Step Diffusion: An Elementary Tutorial

We present an accessible first course on diffusion models and flow matching for machine learning, aimed at a technical audience with no diffusion experience. We try to simplify the mathematical details as much as possible (sometimes heuristically), while retaining enough precision to derive correct algorithms.

Vanishing Gradients in Reinforcement Finetuning of Language Models

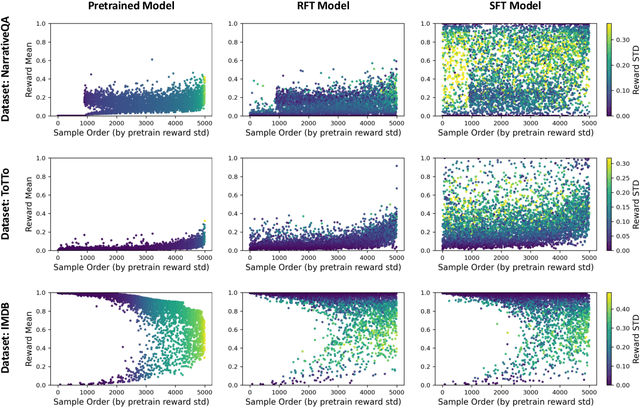
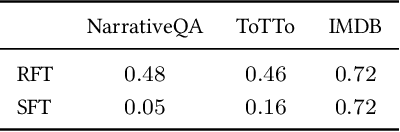
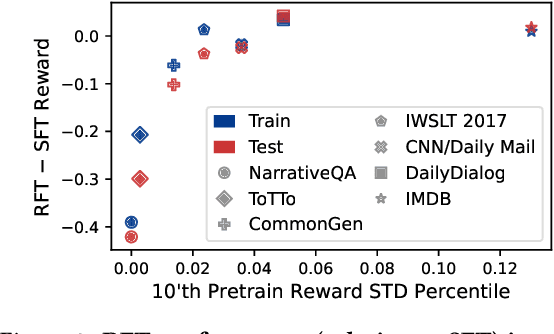
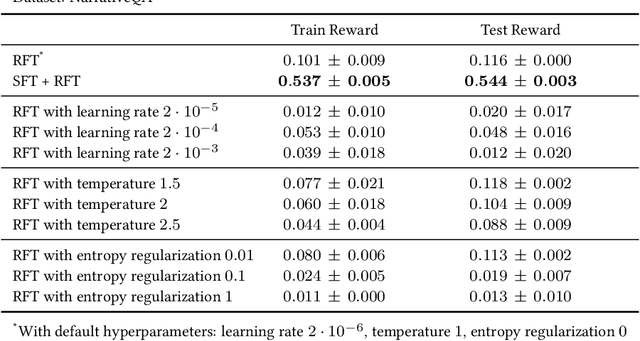
Pretrained language models are commonly aligned with human preferences and downstream tasks via reinforcement finetuning (RFT), which entails maximizing a (possibly learned) reward function using policy gradient algorithms. This work highlights a fundamental optimization obstacle in RFT: we prove that the expected gradient for an input vanishes when its reward standard deviation under the model is small, even if the expected reward is far from optimal. Through experiments on an RFT benchmark and controlled environments, as well as a theoretical analysis, we then demonstrate that vanishing gradients due to small reward standard deviation are prevalent and detrimental, leading to extremely slow reward maximization. Lastly, we explore ways to overcome vanishing gradients in RFT. We find the common practice of an initial supervised finetuning (SFT) phase to be the most promising candidate, which sheds light on its importance in an RFT pipeline. Moreover, we show that a relatively small number of SFT optimization steps on as few as 1% of the input samples can suffice, indicating that the initial SFT phase need not be expensive in terms of compute and data labeling efforts. Overall, our results emphasize that being mindful for inputs whose expected gradient vanishes, as measured by the reward standard deviation, is crucial for successful execution of RFT.

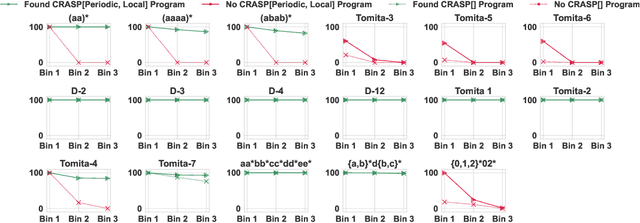
What Algorithms can Transformers Learn? A Study in Length Generalization

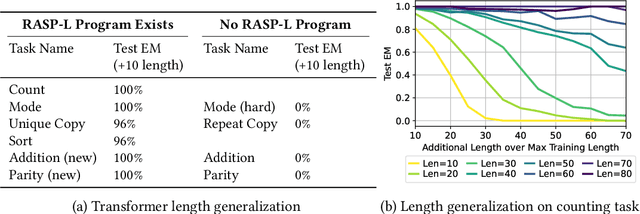
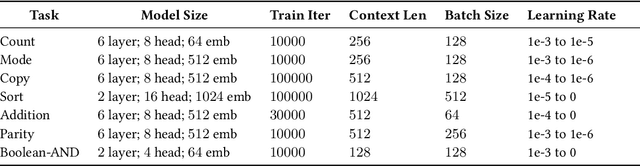
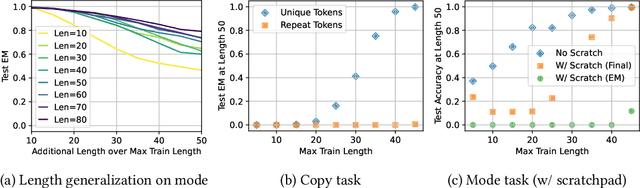
Large language models exhibit surprising emergent generalization properties, yet also struggle on many simple reasoning tasks such as arithmetic and parity. This raises the question of if and when Transformer models can learn the true algorithm for solving a task. We study the scope of Transformers' abilities in the specific setting of length generalization on algorithmic tasks. Here, we propose a unifying framework to understand when and how Transformers can exhibit strong length generalization on a given task. Specifically, we leverage RASP (Weiss et al., 2021) -- a programming language designed for the computational model of a Transformer -- and introduce the RASP-Generalization Conjecture: Transformers tend to length generalize on a task if the task can be solved by a short RASP program which works for all input lengths. This simple conjecture remarkably captures most known instances of length generalization on algorithmic tasks. Moreover, we leverage our insights to drastically improve generalization performance on traditionally hard tasks (such as parity and addition). On the theoretical side, we give a simple example where the "min-degree-interpolator" model of learning from Abbe et al. (2023) does not correctly predict Transformers' out-of-distribution behavior, but our conjecture does. Overall, our work provides a novel perspective on the mechanisms of compositional generalization and the algorithmic capabilities of Transformers.

Predicting Grokking Long Before it Happens: A look into the loss landscape of models which grok

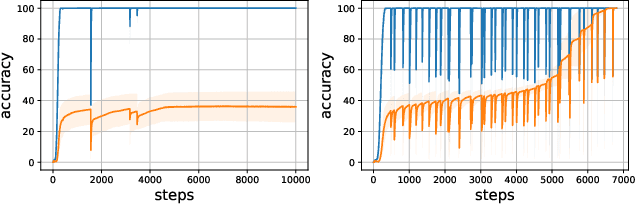
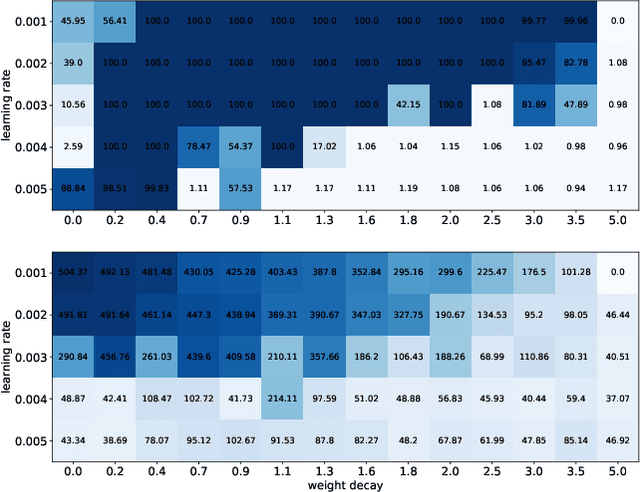
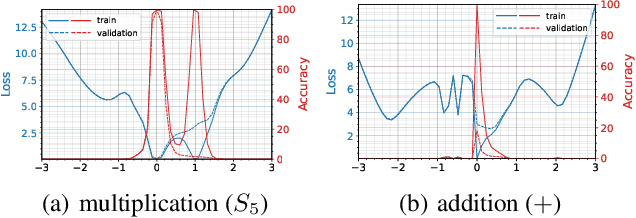
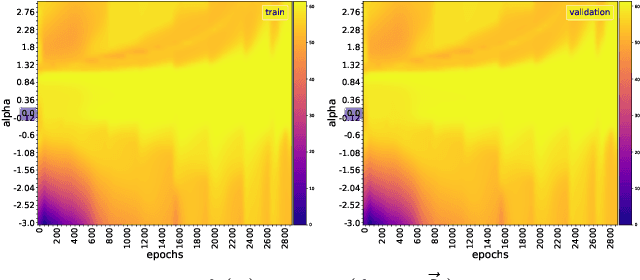
This paper focuses on predicting the occurrence of grokking in neural networks, a phenomenon in which perfect generalization emerges long after signs of overfitting or memorization are observed. It has been reported that grokking can only be observed with certain hyper-parameters. This makes it critical to identify the parameters that lead to grokking. However, since grokking occurs after a large number of epochs, searching for the hyper-parameters that lead to it is time-consuming. In this paper, we propose a low-cost method to predict grokking without training for a large number of epochs. In essence, by studying the learning curve of the first few epochs, we show that one can predict whether grokking will occur later on. Specifically, if certain oscillations occur in the early epochs, one can expect grokking to occur if the model is trained for a much longer period of time. We propose using the spectral signature of a learning curve derived by applying the Fourier transform to quantify the amplitude of low-frequency components to detect the presence of such oscillations. We also present additional experiments aimed at explaining the cause of these oscillations and characterizing the loss landscape.

Teaching Algorithmic Reasoning via In-context Learning

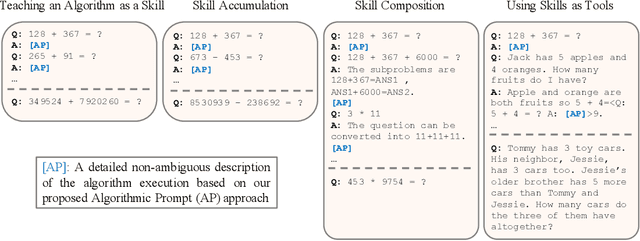
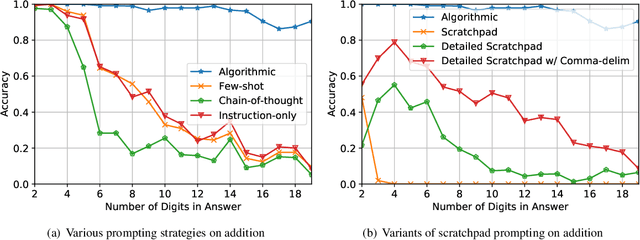
Large language models (LLMs) have shown increasing in-context learning capabilities through scaling up model and data size. Despite this progress, LLMs are still unable to solve algorithmic reasoning problems. While providing a rationale with the final answer has led to further improvements in multi-step reasoning problems, Anil et al. 2022 showed that even simple algorithmic reasoning tasks such as parity are far from solved. In this work, we identify and study four key stages for successfully teaching algorithmic reasoning to LLMs: (1) formulating algorithms as skills, (2) teaching multiple skills simultaneously (skill accumulation), (3) teaching how to combine skills (skill composition) and (4) teaching how to use skills as tools. We show that it is possible to teach algorithmic reasoning to LLMs via in-context learning, which we refer to as algorithmic prompting. We evaluate our approach on a variety of arithmetic and quantitative reasoning tasks, and demonstrate significant boosts in performance over existing prompting techniques. In particular, for long parity, addition, multiplication and subtraction, we achieve an error reduction of approximately 10x, 9x, 5x and 2x respectively compared to the best available baselines.

Fortuitous Forgetting in Connectionist Networks

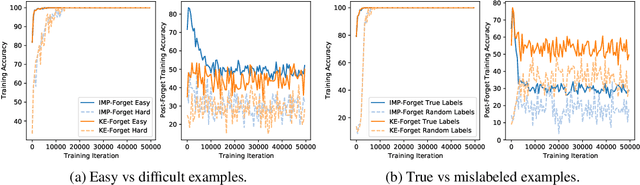
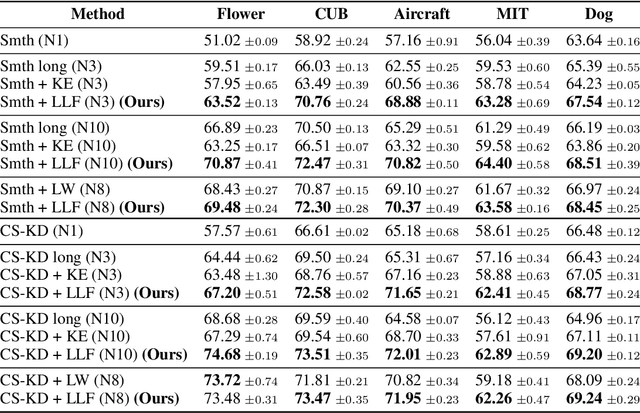
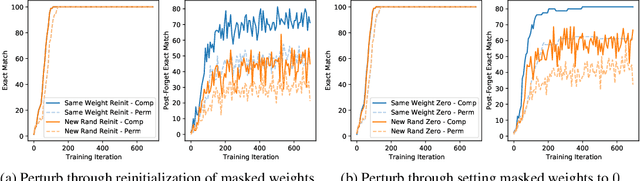
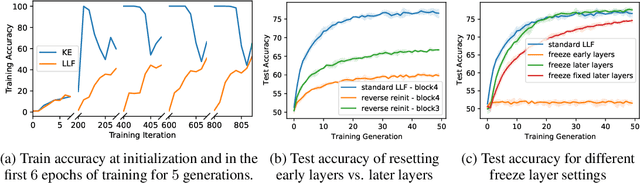
Forgetting is often seen as an unwanted characteristic in both human and machine learning. However, we propose that forgetting can in fact be favorable to learning. We introduce "forget-and-relearn" as a powerful paradigm for shaping the learning trajectories of artificial neural networks. In this process, the forgetting step selectively removes undesirable information from the model, and the relearning step reinforces features that are consistently useful under different conditions. The forget-and-relearn framework unifies many existing iterative training algorithms in the image classification and language emergence literature, and allows us to understand the success of these algorithms in terms of the disproportionate forgetting of undesirable information. We leverage this understanding to improve upon existing algorithms by designing more targeted forgetting operations. Insights from our analysis provide a coherent view on the dynamics of iterative training in neural networks and offer a clear path towards performance improvements.

LCA: Loss Change Allocation for Neural Network Training

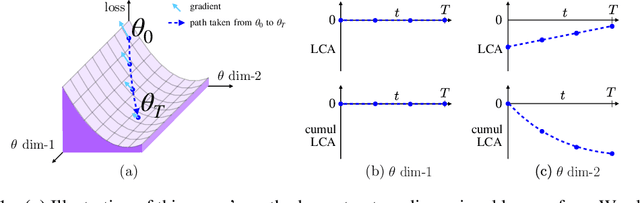
Neural networks enjoy widespread use, but many aspects of their training, representation, and operation are poorly understood. In particular, our view into the training process is limited, with a single scalar loss being the most common viewport into this high-dimensional, dynamic process. We propose a new window into training called Loss Change Allocation (LCA), in which credit for changes to the network loss is conservatively partitioned to the parameters. This measurement is accomplished by decomposing the components of an approximate path integral along the training trajectory using a Runge-Kutta integrator. This rich view shows which parameters are responsible for decreasing or increasing the loss during training, or which parameters "help" or "hurt" the network's learning, respectively. LCA may be summed over training iterations and/or over neurons, channels, or layers for increasingly coarse views. This new measurement device produces several insights into training. (1) We find that barely over 50% of parameters help during any given iteration. (2) Some entire layers hurt overall, moving on average against the training gradient, a phenomenon we hypothesize may be due to phase lag in an oscillatory training process. (3) Finally, increments in learning proceed in a synchronized manner across layers, often peaking on identical iterations.

Deconstructing Lottery Tickets: Zeros, Signs, and the Supermask

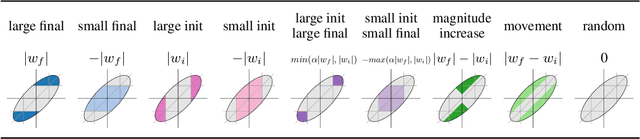
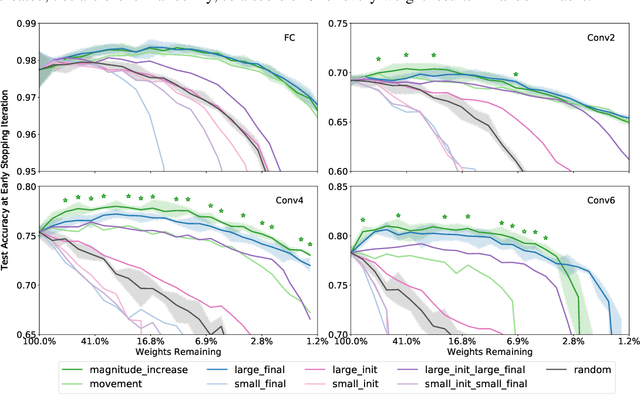
The recent "Lottery Ticket Hypothesis" paper by Frankle & Carbin showed that a simple approach to creating sparse networks (keep the large weights) results in models that are trainable from scratch, but only when starting from the same initial weights. The performance of these networks often exceeds the performance of the non-sparse base model, but for reasons that were not well understood. In this paper we study the three critical components of the Lottery Ticket (LT) algorithm, showing that each may be varied significantly without impacting the overall results. Ablating these factors leads to new insights for why LT networks perform as well as they do. We show why setting weights to zero is important, how signs are all you need to make the re-initialized network train, and why masking behaves like training. Finally, we discover the existence of Supermasks, or masks that can be applied to an untrained, randomly initialized network to produce a model with performance far better than chance (86% on MNIST, 41% on CIFAR-10).