How JEPA Avoids Noisy Features: The Implicit Bias of Deep Linear Self Distillation Networks

Two competing paradigms exist for self-supervised learning of data representations. Joint Embedding Predictive Architecture (JEPA) is a class of architectures in which semantically similar inputs are encoded into representations that are predictive of each other. A recent successful approach that falls under the JEPA framework is self-distillation, where an online encoder is trained to predict the output of the target encoder, sometimes using a lightweight predictor network. This is contrasted with the Masked AutoEncoder (MAE) paradigm, where an encoder and decoder are trained to reconstruct missing parts of the input in the data space rather, than its latent representation. A common motivation for using the JEPA approach over MAE is that the JEPA objective prioritizes abstract features over fine-grained pixel information (which can be unpredictable and uninformative). In this work, we seek to understand the mechanism behind this empirical observation by analyzing the training dynamics of deep linear models. We uncover a surprising mechanism: in a simplified linear setting where both approaches learn similar representations, JEPAs are biased to learn high-influence features, i.e., features characterized by having high regression coefficients. Our results point to a distinct implicit bias of predicting in latent space that may shed light on its success in practice.

Step-by-Step Diffusion: An Elementary Tutorial

We present an accessible first course on diffusion models and flow matching for machine learning, aimed at a technical audience with no diffusion experience. We try to simplify the mathematical details as much as possible (sometimes heuristically), while retaining enough precision to derive correct algorithms.

A new role for circuit expansion for learning in neural networks

Many sensory pathways in the brain rely on sparsely active populations of neurons downstream from the input stimuli. The biological reason for the occurrence of expanded structure in the brain is unclear, but may be because expansion can increase the expressive power of a neural network. In this work, we show that expanding a neural network can improve its generalization performance even in cases in which the expanded structure is pruned after the learning period. To study this setting we use a teacher-student framework where a perceptron teacher network generates labels which are corrupted with small amounts of noise. We then train a student network that is structurally matched to the teacher and can achieve optimal accuracy if given the teacher's synaptic weights. We find that sparse expansion of the input of a student perceptron network both increases its capacity and improves the generalization performance of the network when learning a noisy rule from a teacher perceptron when these expansions are pruned after learning. We find similar behavior when the expanded units are stochastic and uncorrelated with the input and analyze this network in the mean field limit. We show by solving the mean field equations that the generalization error of the stochastic expanded student network continues to drop as the size of the network increases. The improvement in generalization performance occurs despite the increased complexity of the student network relative to the teacher it is trying to learn. We show that this effect is closely related to the addition of slack variables in artificial neural networks and suggest possible implications for artificial and biological neural networks.

Dimensionality compression and expansion in Deep Neural Networks

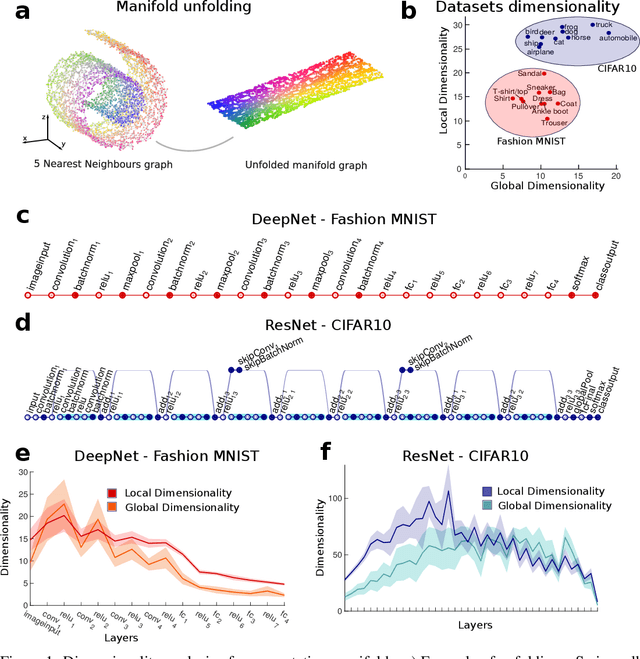
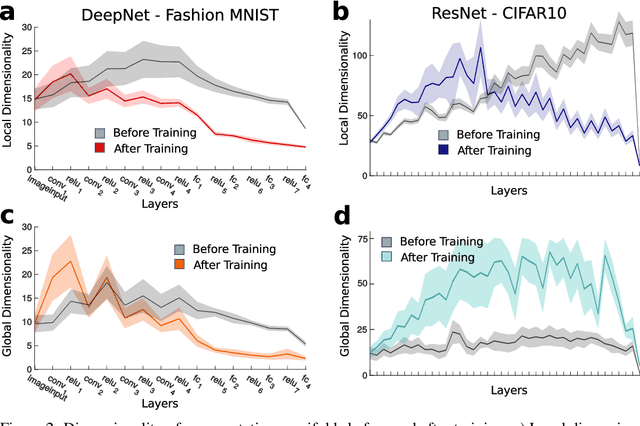
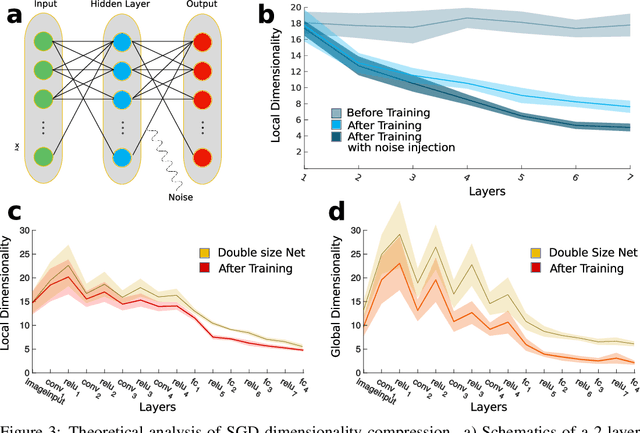
Datasets such as images, text, or movies are embedded in high-dimensional spaces. However, in important cases such as images of objects, the statistical structure in the data constrains samples to a manifold of dramatically lower dimensionality. Learning to identify and extract task-relevant variables from this embedded manifold is crucial when dealing with high-dimensional problems. We find that neural networks are often very effective at solving this task and investigate why. To this end, we apply state-of-the-art techniques for intrinsic dimensionality estimation to show that neural networks learn low-dimensional manifolds in two phases: first, dimensionality expansion driven by feature generation in initial layers, and second, dimensionality compression driven by the selection of task-relevant features in later layers. We model noise generated by Stochastic Gradient Descent and show how this noise balances the dimensionality of neural representations by inducing an effective regularization term in the loss. We highlight the important relationship between low-dimensional compressed representations and generalization properties of the network. Our work contributes by shedding light on the success of deep neural networks in disentangling data in high-dimensional space while achieving good generalization. Furthermore, it invites new learning strategies focused on optimizing measurable geometric properties of learned representations, beginning with their intrinsic dimensionality.

Minnorm training: an algorithm for training over-parameterized deep neural networks

In this work, we propose a new training method for finding minimum weight norm solutions in over-parameterized neural networks (NNs). This method seeks to improve training speed and generalization performance by framing NN training as a constrained optimization problem wherein the sum of the norm of the weights in each layer of the network is minimized, under the constraint of exactly fitting training data. It draws inspiration from support vector machines (SVMs), which are able to generalize well, despite often having an infinite number of free parameters in their primal form, and from recent theoretical generalization bounds on NNs which suggest that lower norm solutions generalize better. To solve this constrained optimization problem, our method employs Lagrange multipliers that act as integrators of error over training and identify `support vector'-like examples. The method can be implemented as a wrapper around gradient based methods and uses standard back-propagation of gradients from the NN for both regression and classification versions of the algorithm. We provide theoretical justifications for the effectiveness of this algorithm in comparison to early stopping and $L_2$-regularization using simple, analytically tractable settings. In particular, we show faster convergence to the max-margin hyperplane in a shallow network (compared to vanilla gradient descent); faster convergence to the minimum-norm solution in a linear chain (compared to $L_2$-regularization); and initialization-independent generalization performance in a deep linear network. Finally, using the MNIST dataset, we demonstrate that this algorithm can boost test accuracy and identify difficult examples in real-world datasets.

An equivalence between high dimensional Bayes optimal inference and M-estimation

When recovering an unknown signal from noisy measurements, the computational difficulty of performing optimal Bayesian MMSE (minimum mean squared error) inference often necessitates the use of maximum a posteriori (MAP) inference, a special case of regularized M-estimation, as a surrogate. However, MAP is suboptimal in high dimensions, when the number of unknown signal components is similar to the number of measurements. In this work we demonstrate, when the signal distribution and the likelihood function associated with the noise are both log-concave, that optimal MMSE performance is asymptotically achievable via another M-estimation procedure. This procedure involves minimizing convex loss and regularizer functions that are nonlinearly smoothed versions of the widely applied MAP optimization problem. Our findings provide a new heuristic derivation and interpretation for recent optimal M-estimators found in the setting of linear measurements and additive noise, and further extend these results to nonlinear measurements with non-additive noise. We numerically demonstrate superior performance of our optimal M-estimators relative to MAP. Overall, at the heart of our work is the revelation of a remarkable equivalence between two seemingly very different computational problems: namely that of high dimensional Bayesian integration underlying MMSE inference, and high dimensional convex optimization underlying M-estimation. In essence we show that the former difficult integral may be computed by solving the latter, simpler optimization problem.

Statistical Mechanics of High-Dimensional Inference

To model modern large-scale datasets, we need efficient algorithms to infer a set of $P$ unknown model parameters from $N$ noisy measurements. What are fundamental limits on the accuracy of parameter inference, given finite signal-to-noise ratios, limited measurements, prior information, and computational tractability requirements? How can we combine prior information with measurements to achieve these limits? Classical statistics gives incisive answers to these questions as the measurement density $\alpha = \frac{N}{P}\rightarrow \infty$. However, these classical results are not relevant to modern high-dimensional inference problems, which instead occur at finite $\alpha$. We formulate and analyze high-dimensional inference as a problem in the statistical physics of quenched disorder. Our analysis uncovers fundamental limits on the accuracy of inference in high dimensions, and reveals that widely cherished inference algorithms like maximum likelihood (ML) and maximum-a posteriori (MAP) inference cannot achieve these limits. We further find optimal, computationally tractable algorithms that can achieve these limits. Intriguingly, in high dimensions, these optimal algorithms become computationally simpler than MAP and ML, while still outperforming them. For example, such optimal algorithms can lead to as much as a 20% reduction in the amount of data to achieve the same performance relative to MAP. Moreover, our analysis reveals simple relations between optimal high dimensional inference and low dimensional scalar Bayesian inference, insights into the nature of generalization and predictive power in high dimensions, information theoretic limits on compressed sensing, phase transitions in quadratic inference, and connections to central mathematical objects in convex optimization theory and random matrix theory.

Statistical mechanics of complex neural systems and high dimensional data

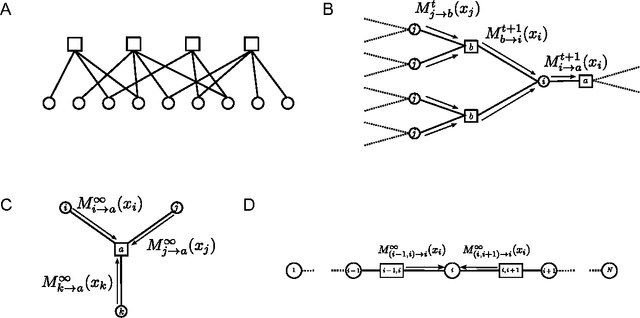
Recent experimental advances in neuroscience have opened new vistas into the immense complexity of neuronal networks. This proliferation of data challenges us on two parallel fronts. First, how can we form adequate theoretical frameworks for understanding how dynamical network processes cooperate across widely disparate spatiotemporal scales to solve important computational problems? And second, how can we extract meaningful models of neuronal systems from high dimensional datasets? To aid in these challenges, we give a pedagogical review of a collection of ideas and theoretical methods arising at the intersection of statistical physics, computer science and neurobiology. We introduce the interrelated replica and cavity methods, which originated in statistical physics as powerful ways to quantitatively analyze large highly heterogeneous systems of many interacting degrees of freedom. We also introduce the closely related notion of message passing in graphical models, which originated in computer science as a distributed algorithm capable of solving large inference and optimization problems involving many coupled variables. We then show how both the statistical physics and computer science perspectives can be applied in a wide diversity of contexts to problems arising in theoretical neuroscience and data analysis. Along the way we discuss spin glasses, learning theory, illusions of structure in noise, random matrices, dimensionality reduction, and compressed sensing, all within the unified formalism of the replica method. Moreover, we review recent conceptual connections between message passing in graphical models, and neural computation and learning. Overall, these ideas illustrate how statistical physics and computer science might provide a lens through which we can uncover emergent computational functions buried deep within the dynamical complexities of neuronal networks.