Identifying the impact of local connectivity patterns on dynamics in excitatory-inhibitory networks

Networks of excitatory and inhibitory (EI) neurons form a canonical circuit in the brain. Seminal theoretical results on dynamics of such networks are based on the assumption that synaptic strengths depend on the type of neurons they connect, but are otherwise statistically independent. Recent synaptic physiology datasets however highlight the prominence of specific connectivity patterns that go well beyond what is expected from independent connections. While decades of influential research have demonstrated the strong role of the basic EI cell type structure, to which extent additional connectivity features influence dynamics remains to be fully determined. Here we examine the effects of pairwise connectivity motifs on the linear dynamics in EI networks using an analytical framework that approximates the connectivity in terms of low-rank structures. This low-rank approximation is based on a mathematical derivation of the dominant eigenvalues of the connectivity matrix and predicts the impact on responses to external inputs of connectivity motifs and their interactions with cell-type structure. Our results reveal that a particular pattern of connectivity, chain motifs, have a much stronger impact on dominant eigenmodes than other pairwise motifs. An overrepresentation of chain motifs induces a strong positive eigenvalue in inhibition-dominated networks and generates a potential instability that requires revisiting the classical excitation-inhibition balance criteria. Examining effects of external inputs, we show that chain motifs can on their own induce paradoxical responses where an increased input to inhibitory neurons leads to a decrease in their activity due to the recurrent feedback. These findings have direct implications for the interpretation of experiments in which responses to optogenetic perturbations are measured and used to infer the dynamical regime of cortical circuits.

Learning to Embed Distributions via Maximum Kernel Entropy

Empirical data can often be considered as samples from a set of probability distributions. Kernel methods have emerged as a natural approach for learning to classify these distributions. Although numerous kernels between distributions have been proposed, applying kernel methods to distribution regression tasks remains challenging, primarily because selecting a suitable kernel is not straightforward. Surprisingly, the question of learning a data-dependent distribution kernel has received little attention. In this paper, we propose a novel objective for the unsupervised learning of data-dependent distribution kernel, based on the principle of entropy maximization in the space of probability measure embeddings. We examine the theoretical properties of the latent embedding space induced by our objective, demonstrating that its geometric structure is well-suited for solving downstream discriminative tasks. Finally, we demonstrate the performance of the learned kernel across different modalities.

A simple connection from loss flatness to compressed representations in neural networks

Deep neural networks' generalization capacity has been studied in a variety of ways, including at least two distinct categories of approach: one based on the shape of the loss landscape in parameter space, and the other based on the structure of the representation manifold in feature space (that is, in the space of unit activities). These two approaches are related, but they are rarely studied together and explicitly connected. Here, we present a simple analysis that makes such a connection. We show that, in the last phase of learning of deep neural networks, compression of the volume of the manifold of neural representations correlates with the flatness of the loss around the minima explored by ongoing parameter optimization. We show that this is predicted by a relatively simple mathematical relationship: loss flatness implies compression of neural representations. Our results build closely on prior work of \citet{ma_linear_2021}, which shows how flatness (i.e., small eigenvalues of the loss Hessian) develops in late phases of learning and lead to robustness to perturbations in network inputs. Moreover, we show there is no similarly direct connection between local dimensionality and sharpness, suggesting that this property may be controlled by different mechanisms than volume and hence may play a complementary role in neural representations. Overall, we advance a dual perspective on generalization in neural networks in both parameter and feature space.

Dimensionality compression and expansion in Deep Neural Networks

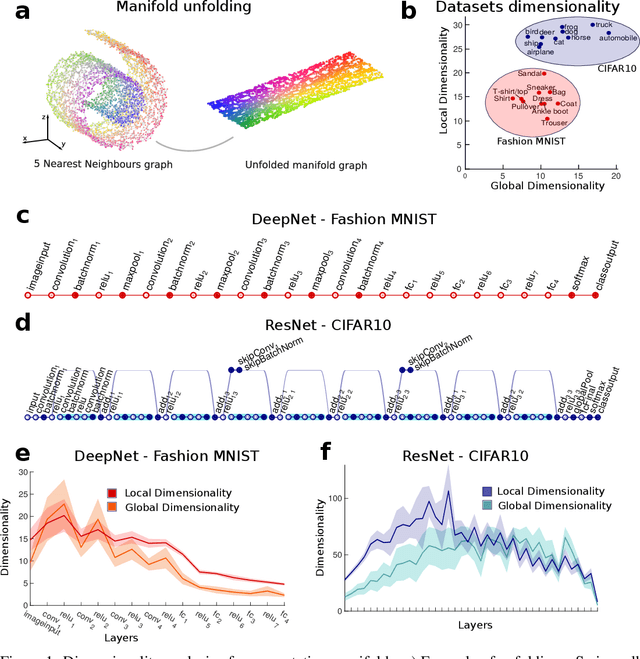
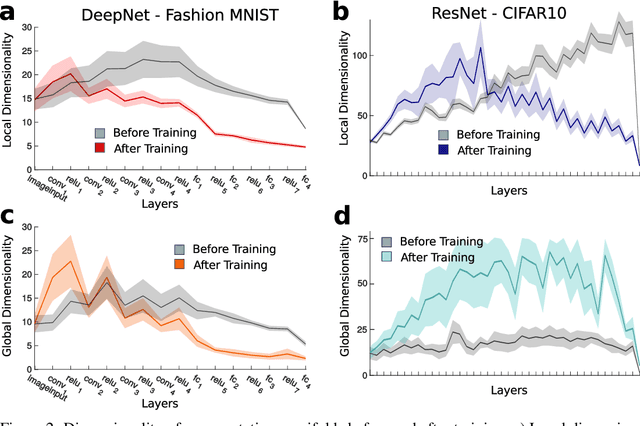
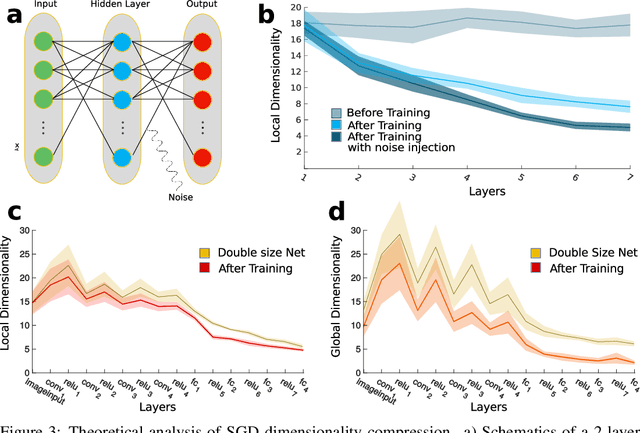
Datasets such as images, text, or movies are embedded in high-dimensional spaces. However, in important cases such as images of objects, the statistical structure in the data constrains samples to a manifold of dramatically lower dimensionality. Learning to identify and extract task-relevant variables from this embedded manifold is crucial when dealing with high-dimensional problems. We find that neural networks are often very effective at solving this task and investigate why. To this end, we apply state-of-the-art techniques for intrinsic dimensionality estimation to show that neural networks learn low-dimensional manifolds in two phases: first, dimensionality expansion driven by feature generation in initial layers, and second, dimensionality compression driven by the selection of task-relevant features in later layers. We model noise generated by Stochastic Gradient Descent and show how this noise balances the dimensionality of neural representations by inducing an effective regularization term in the loss. We highlight the important relationship between low-dimensional compressed representations and generalization properties of the network. Our work contributes by shedding light on the success of deep neural networks in disentangling data in high-dimensional space while achieving good generalization. Furthermore, it invites new learning strategies focused on optimizing measurable geometric properties of learned representations, beginning with their intrinsic dimensionality.