Timothy Moore
Dimensionality compression and expansion in Deep Neural Networks
Jun 02, 2019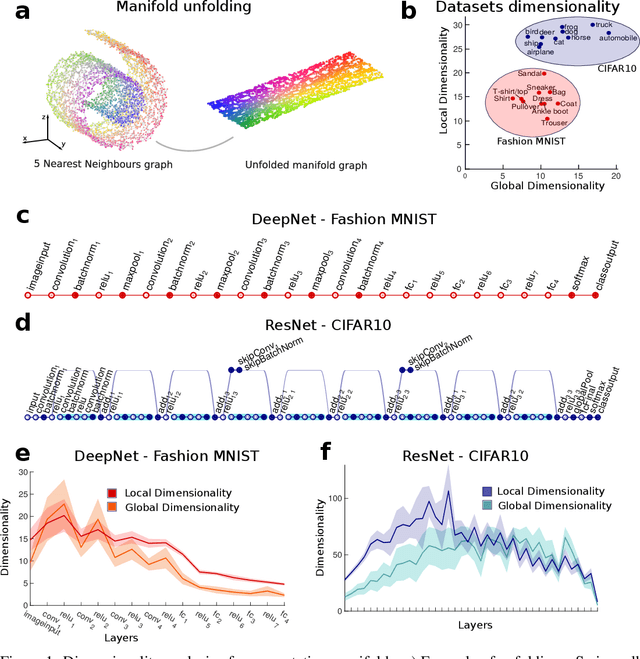
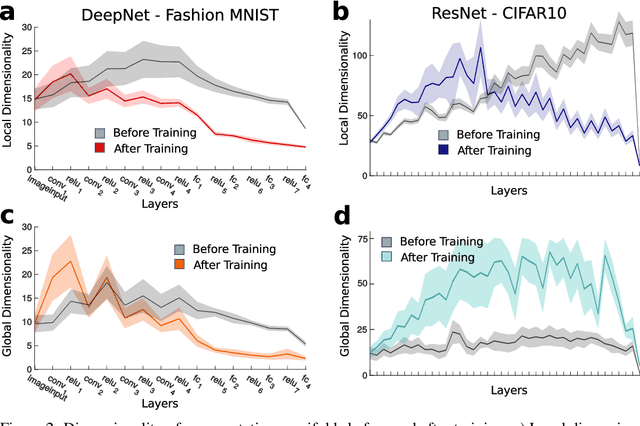
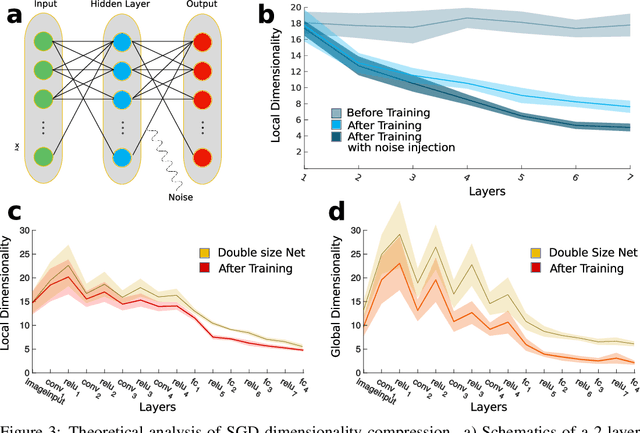
Abstract:Datasets such as images, text, or movies are embedded in high-dimensional spaces. However, in important cases such as images of objects, the statistical structure in the data constrains samples to a manifold of dramatically lower dimensionality. Learning to identify and extract task-relevant variables from this embedded manifold is crucial when dealing with high-dimensional problems. We find that neural networks are often very effective at solving this task and investigate why. To this end, we apply state-of-the-art techniques for intrinsic dimensionality estimation to show that neural networks learn low-dimensional manifolds in two phases: first, dimensionality expansion driven by feature generation in initial layers, and second, dimensionality compression driven by the selection of task-relevant features in later layers. We model noise generated by Stochastic Gradient Descent and show how this noise balances the dimensionality of neural representations by inducing an effective regularization term in the loss. We highlight the important relationship between low-dimensional compressed representations and generalization properties of the network. Our work contributes by shedding light on the success of deep neural networks in disentangling data in high-dimensional space while achieving good generalization. Furthermore, it invites new learning strategies focused on optimizing measurable geometric properties of learned representations, beginning with their intrinsic dimensionality.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge