Capacity of Group-invariant Linear Readouts from Equivariant Representations: How Many Objects can be Linearly Classified Under All Possible Views?

Equivariance has emerged as a desirable property of representations of objects subject to identity-preserving transformations that constitute a group, such as translations and rotations. However, the expressivity of a representation constrained by group equivariance is still not fully understood. We address this gap by providing a generalization of Cover's Function Counting Theorem that quantifies the number of linearly separable and group-invariant binary dichotomies that can be assigned to equivariant representations of objects. We find that the fraction of separable dichotomies is determined by the dimension of the space that is fixed by the group action. We show how this relation extends to operations such as convolutions, element-wise nonlinearities, and global and local pooling. While other operations do not change the fraction of separable dichotomies, local pooling decreases the fraction, despite being a highly nonlinear operation. Finally, we test our theory on intermediate representations of randomly initialized and fully trained convolutional neural networks and find perfect agreement.

Dimensionality compression and expansion in Deep Neural Networks

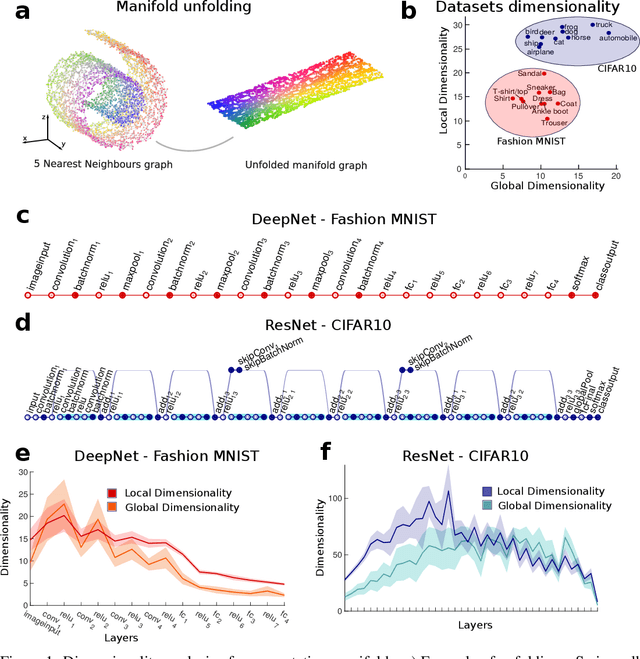
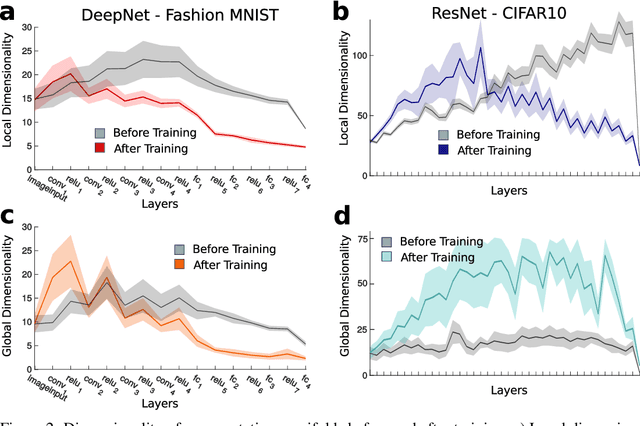
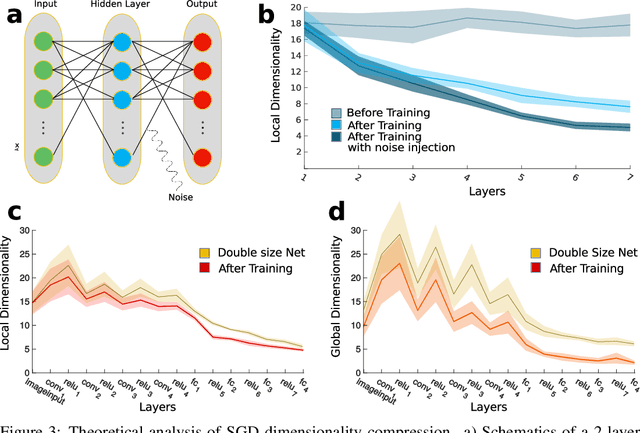
Datasets such as images, text, or movies are embedded in high-dimensional spaces. However, in important cases such as images of objects, the statistical structure in the data constrains samples to a manifold of dramatically lower dimensionality. Learning to identify and extract task-relevant variables from this embedded manifold is crucial when dealing with high-dimensional problems. We find that neural networks are often very effective at solving this task and investigate why. To this end, we apply state-of-the-art techniques for intrinsic dimensionality estimation to show that neural networks learn low-dimensional manifolds in two phases: first, dimensionality expansion driven by feature generation in initial layers, and second, dimensionality compression driven by the selection of task-relevant features in later layers. We model noise generated by Stochastic Gradient Descent and show how this noise balances the dimensionality of neural representations by inducing an effective regularization term in the loss. We highlight the important relationship between low-dimensional compressed representations and generalization properties of the network. Our work contributes by shedding light on the success of deep neural networks in disentangling data in high-dimensional space while achieving good generalization. Furthermore, it invites new learning strategies focused on optimizing measurable geometric properties of learned representations, beginning with their intrinsic dimensionality.