Identifying the impact of local connectivity patterns on dynamics in excitatory-inhibitory networks

Networks of excitatory and inhibitory (EI) neurons form a canonical circuit in the brain. Seminal theoretical results on dynamics of such networks are based on the assumption that synaptic strengths depend on the type of neurons they connect, but are otherwise statistically independent. Recent synaptic physiology datasets however highlight the prominence of specific connectivity patterns that go well beyond what is expected from independent connections. While decades of influential research have demonstrated the strong role of the basic EI cell type structure, to which extent additional connectivity features influence dynamics remains to be fully determined. Here we examine the effects of pairwise connectivity motifs on the linear dynamics in EI networks using an analytical framework that approximates the connectivity in terms of low-rank structures. This low-rank approximation is based on a mathematical derivation of the dominant eigenvalues of the connectivity matrix and predicts the impact on responses to external inputs of connectivity motifs and their interactions with cell-type structure. Our results reveal that a particular pattern of connectivity, chain motifs, have a much stronger impact on dominant eigenmodes than other pairwise motifs. An overrepresentation of chain motifs induces a strong positive eigenvalue in inhibition-dominated networks and generates a potential instability that requires revisiting the classical excitation-inhibition balance criteria. Examining effects of external inputs, we show that chain motifs can on their own induce paradoxical responses where an increased input to inhibitory neurons leads to a decrease in their activity due to the recurrent feedback. These findings have direct implications for the interpretation of experiments in which responses to optogenetic perturbations are measured and used to infer the dynamical regime of cortical circuits.

Attention for Causal Relationship Discovery from Biological Neural Dynamics

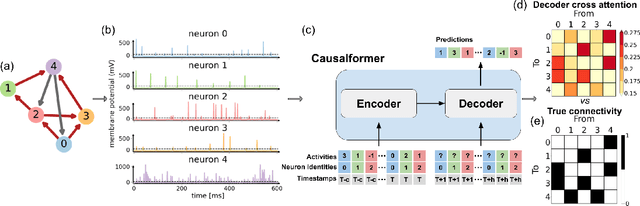
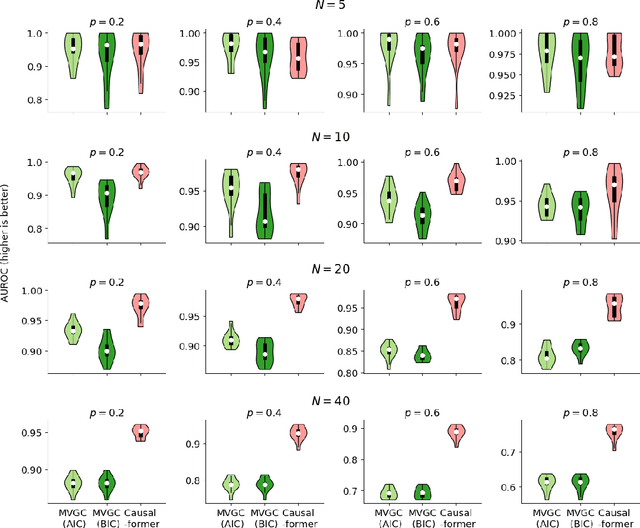
This paper explores the potential of the transformer models for learning Granger causality in networks with complex nonlinear dynamics at every node, as in neurobiological and biophysical networks. Our study primarily focuses on a proof-of-concept investigation based on simulated neural dynamics, for which the ground-truth causality is known through the underlying connectivity matrix. For transformer models trained to forecast neuronal population dynamics, we show that the cross attention module effectively captures the causal relationship among neurons, with an accuracy equal or superior to that for the most popular Granger causality analysis method. While we acknowledge that real-world neurobiology data will bring further challenges, including dynamic connectivity and unobserved variability, this research offers an encouraging preliminary glimpse into the utility of the transformer model for causal representation learning in neuroscience.

Evolutionary algorithms as an alternative to backpropagation for supervised training of Biophysical Neural Networks and Neural ODEs

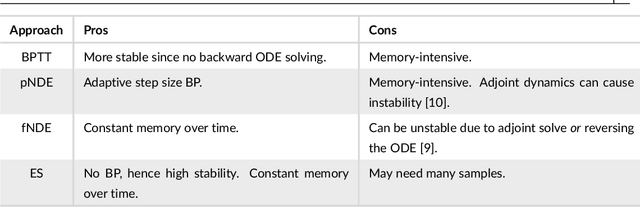
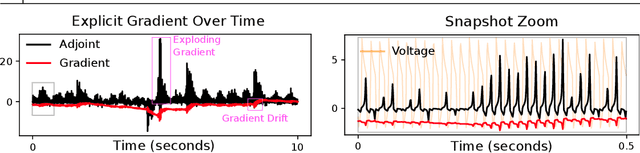
Training networks consisting of biophysically accurate neuron models could allow for new insights into how brain circuits can organize and solve tasks. We begin by analyzing the extent to which the central algorithm for neural network learning -- stochastic gradient descent through backpropagation (BP) -- can be used to train such networks. We find that properties of biophysically based neural network models needed for accurate modelling such as stiffness, high nonlinearity and long evaluation timeframes relative to spike times makes BP unstable and divergent in a variety of cases. To address these instabilities and inspired by recent work, we investigate the use of "gradient-estimating" evolutionary algorithms (EAs) for training biophysically based neural networks. We find that EAs have several advantages making them desirable over direct BP, including being forward-pass only, robust to noisy and rigid losses, allowing for discrete loss formulations, and potentially facilitating a more global exploration of parameters. We apply our method to train a recurrent network of Morris-Lecar neuron models on a stimulus integration and working memory task, and show how it can succeed in cases where direct BP is inapplicable. To expand on the viability of EAs in general, we apply them to a general neural ODE problem and a stiff neural ODE benchmark and find again that EAs can out-perform direct BP here, especially for the over-parameterized regime. Our findings suggest that biophysical neurons could provide useful benchmarks for testing the limits of BP-adjacent methods, and demonstrate the viability of EAs for training networks with complex components.

How connectivity structure shapes rich and lazy learning in neural circuits

In theoretical neuroscience, recent work leverages deep learning tools to explore how some network attributes critically influence its learning dynamics. Notably, initial weight distributions with small (resp. large) variance may yield a rich (resp. lazy) regime, where significant (resp. minor) changes to network states and representation are observed over the course of learning. However, in biology, neural circuit connectivity generally has a low-rank structure and therefore differs markedly from the random initializations generally used for these studies. As such, here we investigate how the structure of the initial weights, in particular their effective rank, influences the network learning regime. Through both empirical and theoretical analyses, we discover that high-rank initializations typically yield smaller network changes indicative of lazier learning, a finding we also confirm with experimentally-driven initial connectivity in recurrent neural networks. Conversely, low-rank initialization biases learning towards richer learning. Importantly, however, as an exception to this rule, we find lazier learning can still occur with a low-rank initialization that aligns with task and data statistics. Our research highlights the pivotal role of initial weight structures in shaping learning regimes, with implications for metabolic costs of plasticity and risks of catastrophic forgetting.

A simple connection from loss flatness to compressed representations in neural networks

Deep neural networks' generalization capacity has been studied in a variety of ways, including at least two distinct categories of approach: one based on the shape of the loss landscape in parameter space, and the other based on the structure of the representation manifold in feature space (that is, in the space of unit activities). These two approaches are related, but they are rarely studied together and explicitly connected. Here, we present a simple analysis that makes such a connection. We show that, in the last phase of learning of deep neural networks, compression of the volume of the manifold of neural representations correlates with the flatness of the loss around the minima explored by ongoing parameter optimization. We show that this is predicted by a relatively simple mathematical relationship: loss flatness implies compression of neural representations. Our results build closely on prior work of \citet{ma_linear_2021}, which shows how flatness (i.e., small eigenvalues of the loss Hessian) develops in late phases of learning and lead to robustness to perturbations in network inputs. Moreover, we show there is no similarly direct connection between local dimensionality and sharpness, suggesting that this property may be controlled by different mechanisms than volume and hence may play a complementary role in neural representations. Overall, we advance a dual perspective on generalization in neural networks in both parameter and feature space.

Expressive probabilistic sampling in recurrent neural networks

In sampling-based Bayesian models of brain function, neural activities are assumed to be samples from probability distributions that the brain uses for probabilistic computation. However, a comprehensive understanding of how mechanistic models of neural dynamics can sample from arbitrary distributions is still lacking. We use tools from functional analysis and stochastic differential equations to explore the minimum architectural requirements for $\textit{recurrent}$ neural circuits to sample from complex distributions. We first consider the traditional sampling model consisting of a network of neurons whose outputs directly represent the samples (sampler-only network). We argue that synaptic current and firing-rate dynamics in the traditional model have limited capacity to sample from a complex probability distribution. We show that the firing rate dynamics of a recurrent neural circuit with a separate set of output units can sample from an arbitrary probability distribution. We call such circuits reservoir-sampler networks (RSNs). We propose an efficient training procedure based on denoising score matching that finds recurrent and output weights such that the RSN implements Langevin sampling. We empirically demonstrate our model's ability to sample from several complex data distributions using the proposed neural dynamics and discuss its applicability to developing the next generation of sampling-based brain models.

Biologically-plausible backpropagation through arbitrary timespans via local neuromodulators

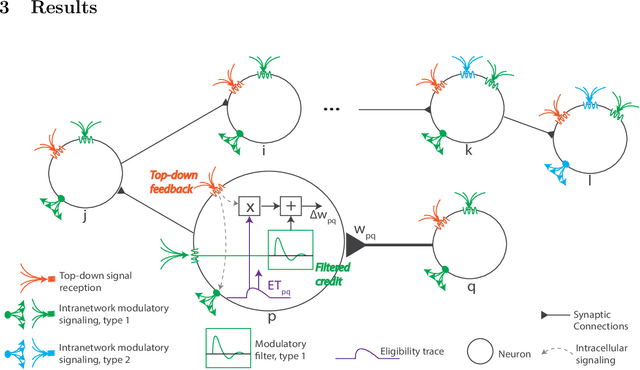
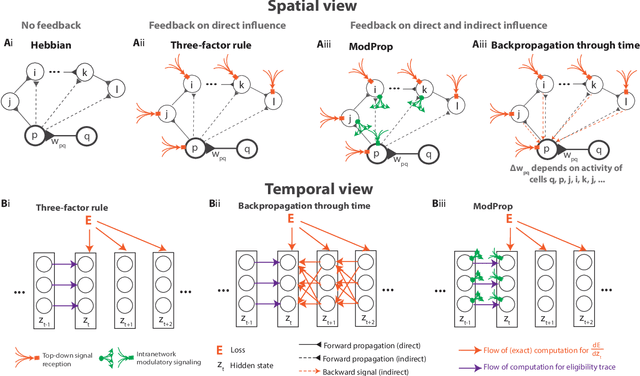
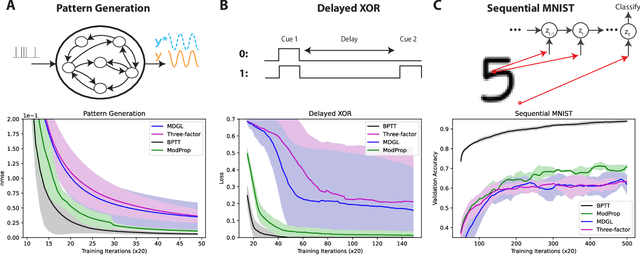
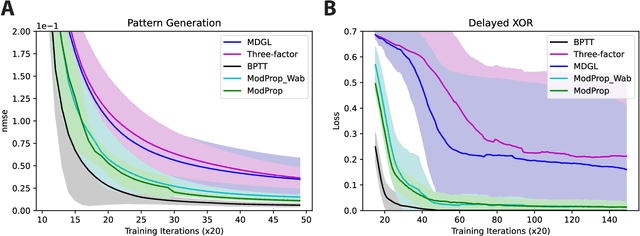
The spectacular successes of recurrent neural network models where key parameters are adjusted via backpropagation-based gradient descent have inspired much thought as to how biological neuronal networks might solve the corresponding synaptic credit assignment problem. There is so far little agreement, however, as to how biological networks could implement the necessary backpropagation through time, given widely recognized constraints of biological synaptic network signaling architectures. Here, we propose that extra-synaptic diffusion of local neuromodulators such as neuropeptides may afford an effective mode of backpropagation lying within the bounds of biological plausibility. Going beyond existing temporal truncation-based gradient approximations, our approximate gradient-based update rule, ModProp, propagates credit information through arbitrary time steps. ModProp suggests that modulatory signals can act on receiving cells by convolving their eligibility traces via causal, time-invariant and synapse-type-specific filter taps. Our mathematical analysis of ModProp learning, together with simulation results on benchmark temporal tasks, demonstrate the advantage of ModProp over existing biologically-plausible temporal credit assignment rules. These results suggest a potential neuronal mechanism for signaling credit information related to recurrent interactions over a longer time horizon. Finally, we derive an in-silico implementation of ModProp that could serve as a low-complexity and causal alternative to backpropagation through time.

Beyond accuracy: generalization properties of bio-plausible temporal credit assignment rules

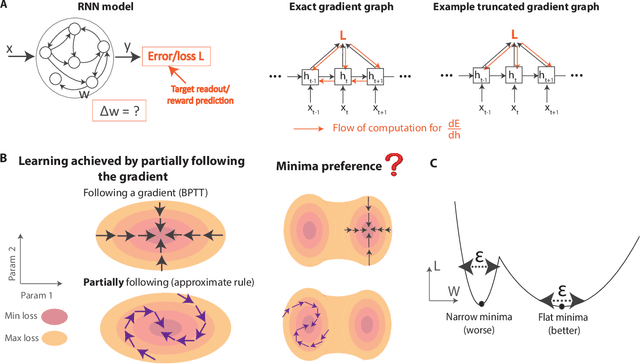
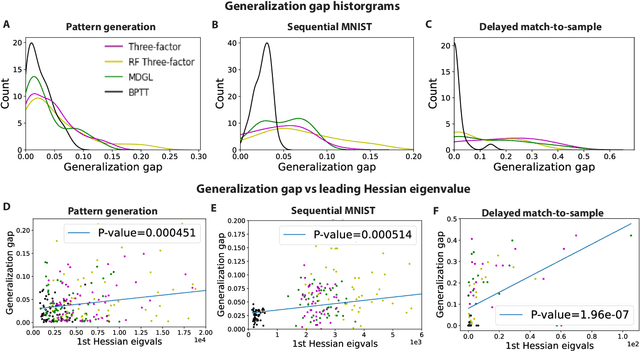
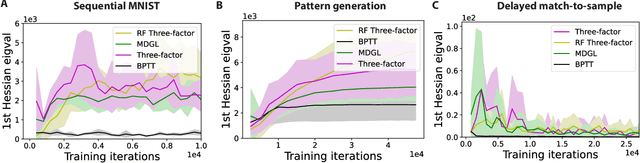
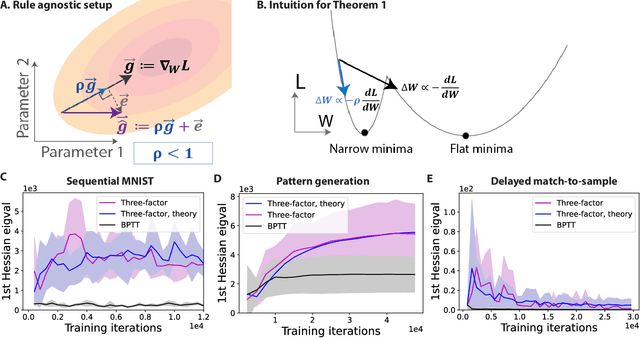
To unveil how the brain learns, ongoing work seeks biologically-plausible approximations of gradient descent algorithms for training recurrent neural networks (RNNs). Yet, beyond task accuracy, it is unclear if such learning rules converge to solutions that exhibit different levels of generalization than their nonbiologically-plausible counterparts. Leveraging results from deep learning theory based on loss landscape curvature, we ask: how do biologically-plausible gradient approximations affect generalization? We first demonstrate that state-of-the-art biologically-plausible learning rules for training RNNs exhibit worse and more variable generalization performance compared to their machine learning counterparts that follow the true gradient more closely. Next, we verify that such generalization performance is correlated significantly with loss landscape curvature, and we show that biologically-plausible learning rules tend to approach high-curvature regions in synaptic weight space. Using tools from dynamical systems, we derive theoretical arguments and present a theorem explaining this phenomenon. This predicts our numerical results, and explains why biologically-plausible rules lead to worse and more variable generalization properties. Finally, we suggest potential remedies that could be used by the brain to mitigate this effect. To our knowledge, our analysis is the first to identify the reason for this generalization gap between artificial and biologically-plausible learning rules, which can help guide future investigations into how the brain learns solutions that generalize.

Dimensionality compression and expansion in Deep Neural Networks

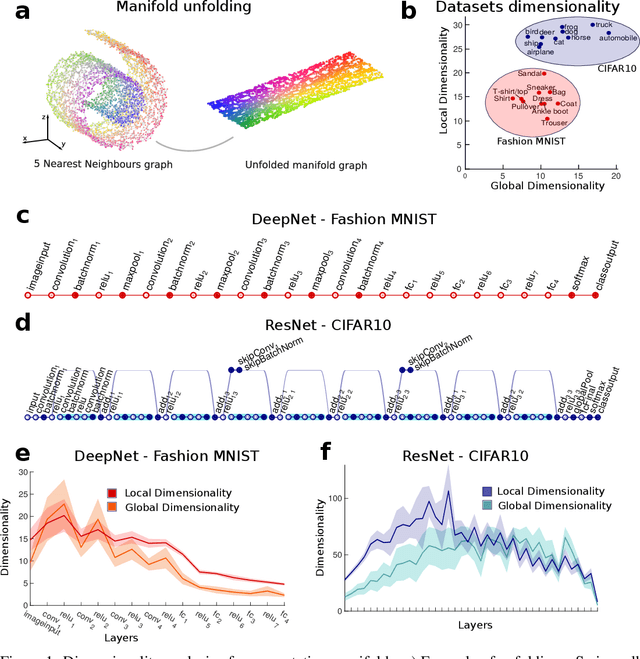
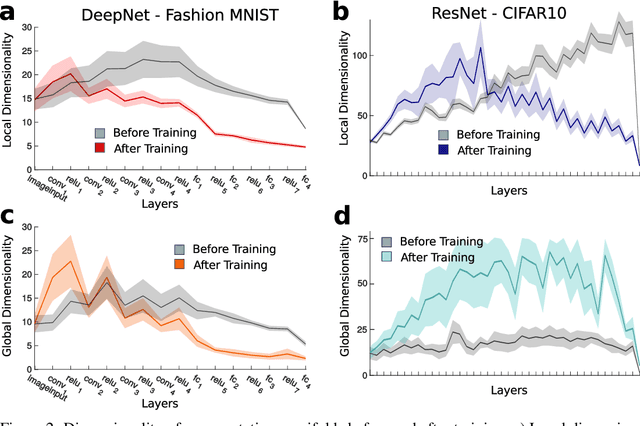
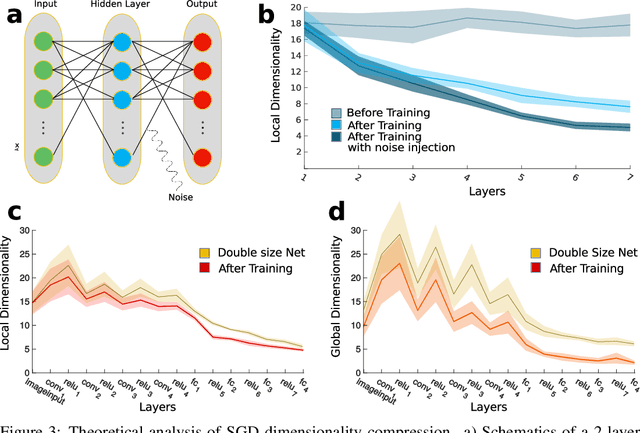
Datasets such as images, text, or movies are embedded in high-dimensional spaces. However, in important cases such as images of objects, the statistical structure in the data constrains samples to a manifold of dramatically lower dimensionality. Learning to identify and extract task-relevant variables from this embedded manifold is crucial when dealing with high-dimensional problems. We find that neural networks are often very effective at solving this task and investigate why. To this end, we apply state-of-the-art techniques for intrinsic dimensionality estimation to show that neural networks learn low-dimensional manifolds in two phases: first, dimensionality expansion driven by feature generation in initial layers, and second, dimensionality compression driven by the selection of task-relevant features in later layers. We model noise generated by Stochastic Gradient Descent and show how this noise balances the dimensionality of neural representations by inducing an effective regularization term in the loss. We highlight the important relationship between low-dimensional compressed representations and generalization properties of the network. Our work contributes by shedding light on the success of deep neural networks in disentangling data in high-dimensional space while achieving good generalization. Furthermore, it invites new learning strategies focused on optimizing measurable geometric properties of learned representations, beginning with their intrinsic dimensionality.