Hierarchy of chaotic dynamics in random modular networks

We introduce a model of randomly connected neural populations and study its dynamics by means of the dynamical mean-field theory and simulations. Our analysis uncovers a rich phase diagram, featuring high- and low-dimensional chaotic phases, separated by a crossover region characterized by low values of the maximal Lyapunov exponent and participation ratio dimension, but with high and rapidly changing values of the Lyapunov dimension. Counterintuitively, chaos can be attenuated by either adding noise to strongly modular connectivity or by introducing modularity into random connectivity. Extending the model to include a multilevel, hierarchical connectivity reveals that a loose balance between activities across levels drives the system towards the edge of chaos.

How connectivity structure shapes rich and lazy learning in neural circuits

In theoretical neuroscience, recent work leverages deep learning tools to explore how some network attributes critically influence its learning dynamics. Notably, initial weight distributions with small (resp. large) variance may yield a rich (resp. lazy) regime, where significant (resp. minor) changes to network states and representation are observed over the course of learning. However, in biology, neural circuit connectivity generally has a low-rank structure and therefore differs markedly from the random initializations generally used for these studies. As such, here we investigate how the structure of the initial weights, in particular their effective rank, influences the network learning regime. Through both empirical and theoretical analyses, we discover that high-rank initializations typically yield smaller network changes indicative of lazier learning, a finding we also confirm with experimentally-driven initial connectivity in recurrent neural networks. Conversely, low-rank initialization biases learning towards richer learning. Importantly, however, as an exception to this rule, we find lazier learning can still occur with a low-rank initialization that aligns with task and data statistics. Our research highlights the pivotal role of initial weight structures in shaping learning regimes, with implications for metabolic costs of plasticity and risks of catastrophic forgetting.

Biologically-plausible backpropagation through arbitrary timespans via local neuromodulators

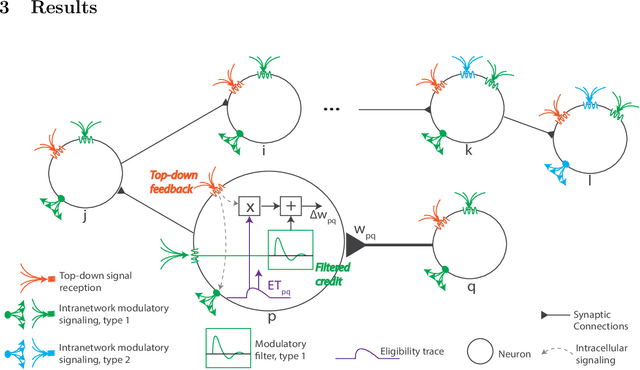
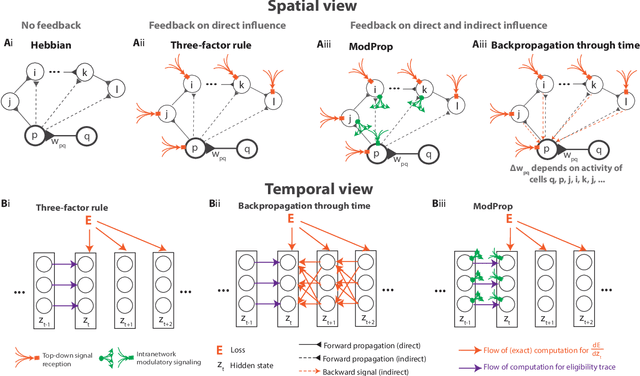
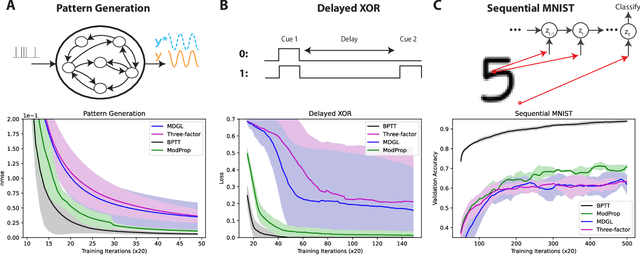
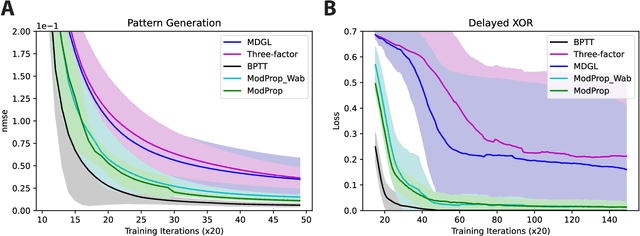
The spectacular successes of recurrent neural network models where key parameters are adjusted via backpropagation-based gradient descent have inspired much thought as to how biological neuronal networks might solve the corresponding synaptic credit assignment problem. There is so far little agreement, however, as to how biological networks could implement the necessary backpropagation through time, given widely recognized constraints of biological synaptic network signaling architectures. Here, we propose that extra-synaptic diffusion of local neuromodulators such as neuropeptides may afford an effective mode of backpropagation lying within the bounds of biological plausibility. Going beyond existing temporal truncation-based gradient approximations, our approximate gradient-based update rule, ModProp, propagates credit information through arbitrary time steps. ModProp suggests that modulatory signals can act on receiving cells by convolving their eligibility traces via causal, time-invariant and synapse-type-specific filter taps. Our mathematical analysis of ModProp learning, together with simulation results on benchmark temporal tasks, demonstrate the advantage of ModProp over existing biologically-plausible temporal credit assignment rules. These results suggest a potential neuronal mechanism for signaling credit information related to recurrent interactions over a longer time horizon. Finally, we derive an in-silico implementation of ModProp that could serve as a low-complexity and causal alternative to backpropagation through time.

Convolutional neural networks with extra-classical receptive fields

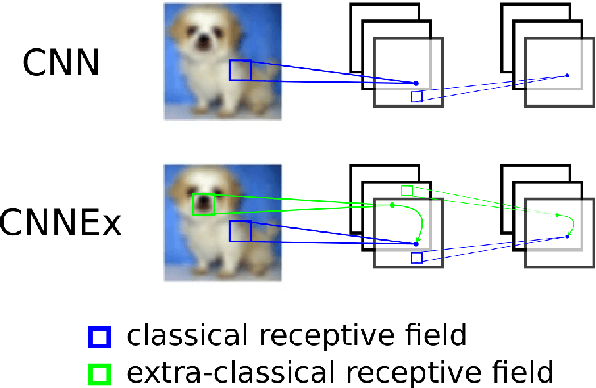
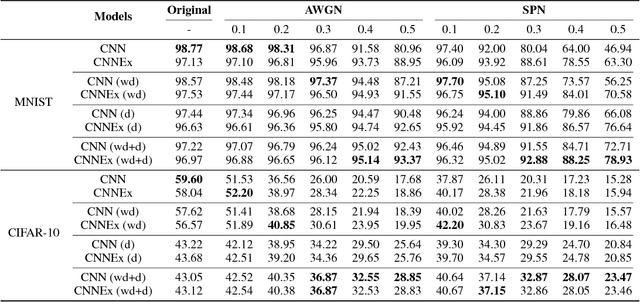
Convolutional neural networks (CNNs) have had great success in many real-world applications and have also been used to model visual processing in the brain. However, these networks are quite brittle - small changes in the input image can dramatically change a network's output prediction. In contrast to what is known from biology, these networks largely rely on feedforward connections, ignoring the influence of recurrent connections. They also focus on supervised rather than unsupervised learning. To address these issues, we combine traditional supervised learning via backpropagation with a specialized unsupervised learning rule to learn lateral connections between neurons within a convolutional neural network. These connections have been shown to optimally integrate information from the surround, generating extra-classical receptive fields for the neurons in our new proposed model (CNNEx). Models with optimal lateral connections are more robust to noise and achieve better performance on noisy versions of the MNIST and CIFAR-10 datasets. Resistance to noise can be further improved by combining our model with additional regularization techniques such as dropout and weight decay. Although the image statistics of MNIST and CIFAR-10 differ greatly, the same unsupervised learning rule generalized to both datasets. Our results demonstrate the potential usefulness of combining supervised and unsupervised learning techniques and suggest that the integration of lateral connections into convolutional neural networks is an important area of future research.