A Fokker-Planck-Based Loss Function that Bridges Dynamics with Density Estimation

We have derived a novel loss function from the Fokker-Planck equation that links dynamical system models with their probability density functions, demonstrating its utility in model identification and density estimation. In the first application, we show that this loss function can enable the extraction of dynamical parameters from non-temporal datasets, including timestamp-free measurements from steady non-equilibrium systems such as noisy Lorenz systems and gene regulatory networks. In the second application, when coupled with a density estimator, this loss facilitates density estimation when the dynamic equations are known. For density estimation, we propose a density estimator that integrates a Gaussian Mixture Model with a normalizing flow model. It simultaneously estimates normalized density, energy, and score functions from both empirical data and dynamics. It is compatible with a variety of data-based training methodologies, including maximum likelihood and score matching. It features a latent space akin to a modern Hopfield network, where the inherent Hopfield energy effectively assigns low densities to sparsely populated data regions, addressing common challenges in neural density estimators. Additionally, this Hopfield-like energy enables direct and rapid data manipulation through the Concave-Convex Procedure (CCCP) rule, facilitating tasks such as denoising and clustering. Our work demonstrates a principled framework for leveraging the complex interdependencies between dynamics and density estimation, as illustrated through synthetic examples that clarify the underlying theoretical intuitions.

Hierarchy of chaotic dynamics in random modular networks

We introduce a model of randomly connected neural populations and study its dynamics by means of the dynamical mean-field theory and simulations. Our analysis uncovers a rich phase diagram, featuring high- and low-dimensional chaotic phases, separated by a crossover region characterized by low values of the maximal Lyapunov exponent and participation ratio dimension, but with high and rapidly changing values of the Lyapunov dimension. Counterintuitively, chaos can be attenuated by either adding noise to strongly modular connectivity or by introducing modularity into random connectivity. Extending the model to include a multilevel, hierarchical connectivity reveals that a loose balance between activities across levels drives the system towards the edge of chaos.

A Novel Pseudo Nearest Neighbor Classification Method Using Local Harmonic Mean Distance

In the realm of machine learning, the KNN classification algorithm is widely recognized for its simplicity and efficiency. However, its sensitivity to the K value poses challenges, especially with small sample sizes or outliers, impacting classification performance. This article introduces a novel KNN-based classifier called LMPHNN (Novel Pseudo Nearest Neighbor Classification Method Using Local Harmonic Mean Distance). LMPHNN leverages harmonic mean distance (HMD) to improve classification performance based on LMPNN rules and HMD. The classifier begins by identifying k nearest neighbors for each class and generates distinct local vectors as prototypes. Pseudo nearest neighbors (PNNs) are then created based on the local mean for each class, determined by comparing the HMD of the sample with the initial k group. Classification is determined by calculating the Euclidean distance between the query sample and PNNs, based on the local mean of these categories. Extensive experiments on various real UCI datasets and combined datasets compare LMPHNN with seven KNN-based classifiers, using precision, recall, accuracy, and F1 as evaluation metrics. LMPHNN achieves an average precision of 97%, surpassing other methods by 14%. The average recall improves by 12%, with an average accuracy enhancement of 5%. Additionally, LMPHNN demonstrates a 13% higher average F1 value compared to other methods. In summary, LMPHNN outperforms other classifiers, showcasing lower sensitivity with small sample sizes.

Learning Continuous Chaotic Attractors with a Reservoir Computer

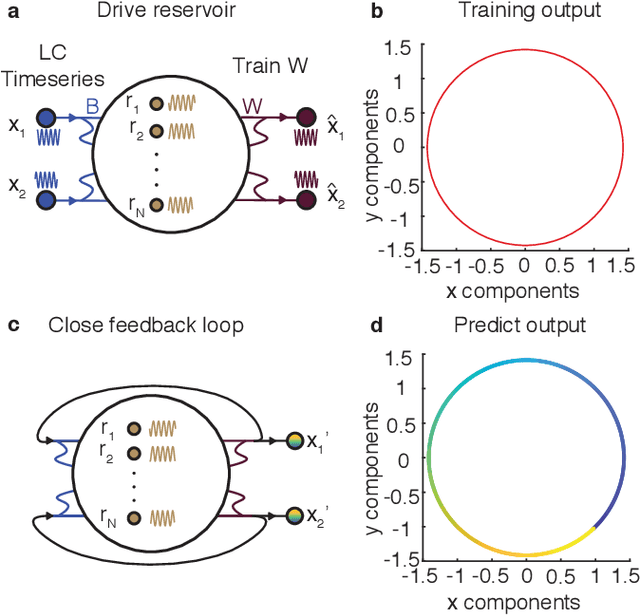
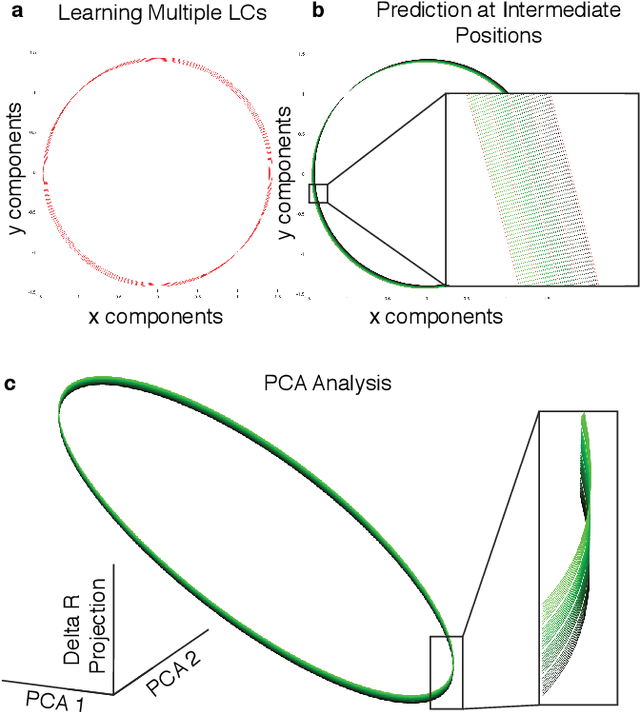
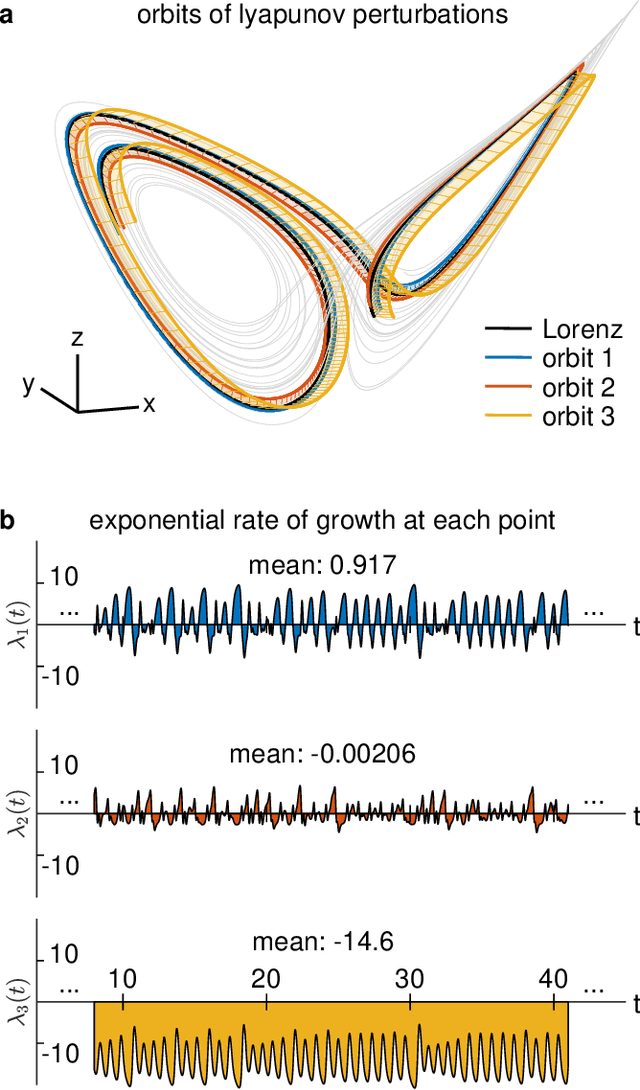
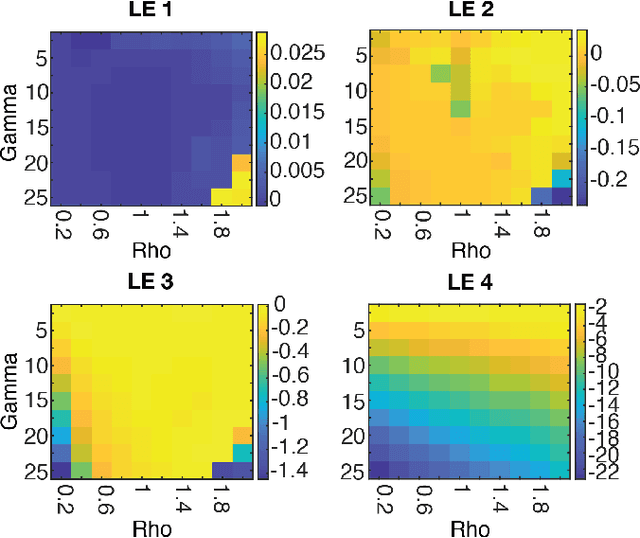
Neural systems are well known for their ability to learn and store information as memories. Even more impressive is their ability to abstract these memories to create complex internal representations, enabling advanced functions such as the spatial manipulation of mental representations. While recurrent neural networks (RNNs) are capable of representing complex information, the exact mechanisms of how dynamical neural systems perform abstraction are still not well-understood, thereby hindering the development of more advanced functions. Here, we train a 1000-neuron RNN -- a reservoir computer (RC) -- to abstract a continuous dynamical attractor memory from isolated examples of dynamical attractor memories. Further, we explain the abstraction mechanism with new theory. By training the RC on isolated and shifted examples of either stable limit cycles or chaotic Lorenz attractors, the RC learns a continuum of attractors, as quantified by an extra Lyapunov exponent equal to zero. We propose a theoretical mechanism of this abstraction by combining ideas from differentiable generalized synchronization and feedback dynamics. Our results quantify abstraction in simple neural systems, enabling us to design artificial RNNs for abstraction, and leading us towards a neural basis of abstraction.

Teaching Recurrent Neural Networks to Modify Chaotic Memories by Example

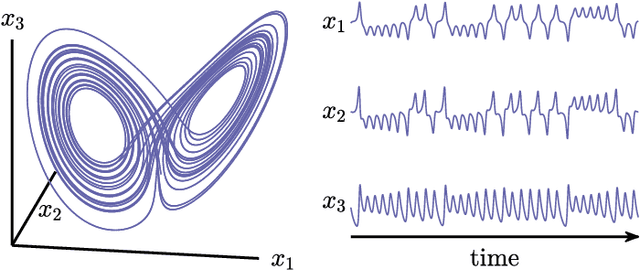
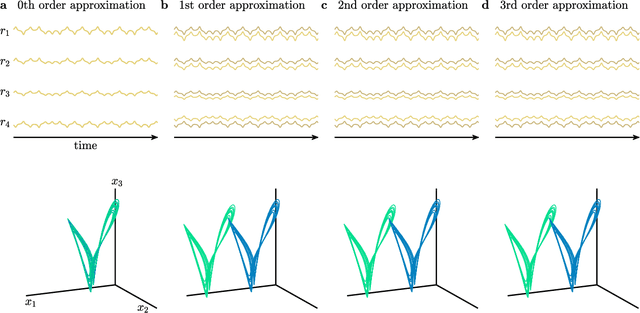
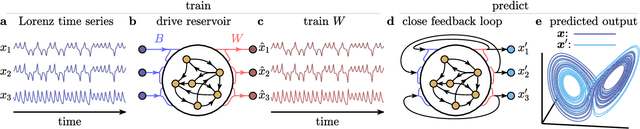
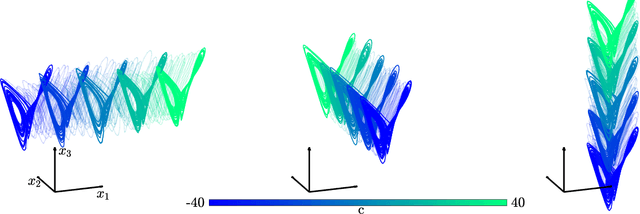
The ability to store and manipulate information is a hallmark of computational systems. Whereas computers are carefully engineered to represent and perform mathematical operations on structured data, neurobiological systems perform analogous functions despite flexible organization and unstructured sensory input. Recent efforts have made progress in modeling the representation and recall of information in neural systems. However, precisely how neural systems learn to modify these representations remains far from understood. Here we demonstrate that a recurrent neural network (RNN) can learn to modify its representation of complex information using only examples, and we explain the associated learning mechanism with new theory. Specifically, we drive an RNN with examples of translated, linearly transformed, or pre-bifurcated time series from a chaotic Lorenz system, alongside an additional control signal that changes value for each example. By training the network to replicate the Lorenz inputs, it learns to autonomously evolve about a Lorenz-shaped manifold. Additionally, it learns to continuously interpolate and extrapolate the translation, transformation, and bifurcation of this representation far beyond the training data by changing the control signal. Finally, we provide a mechanism for how these computations are learned, and demonstrate that a single network can simultaneously learn multiple computations. Together, our results provide a simple but powerful mechanism by which an RNN can learn to manipulate internal representations of complex information, allowing for the principled study and precise design of RNNs.