Is the brain macroscopically linear? A system identification of resting state dynamics

A central challenge in the computational modeling of neural dynamics is the trade-off between accuracy and simplicity. At the level of individual neurons, nonlinear dynamics are both experimentally established and essential for neuronal functioning. An implicit assumption has thus formed that an accurate computational model of whole-brain dynamics must also be highly nonlinear, whereas linear models may provide a first-order approximation. Here, we provide a rigorous and data-driven investigation of this hypothesis at the level of whole-brain blood-oxygen-level-dependent (BOLD) and macroscopic field potential dynamics by leveraging the theory of system identification. Using functional MRI (fMRI) and intracranial EEG (iEEG), we model the resting state activity of 700 subjects in the Human Connectome Project (HCP) and 122 subjects from the Restoring Active Memory (RAM) project using state-of-the-art linear and nonlinear model families. We assess relative model fit using predictive power, computational complexity, and the extent of residual dynamics unexplained by the model. Contrary to our expectations, linear auto-regressive models achieve the best measures across all three metrics, eliminating the trade-off between accuracy and simplicity. To understand and explain this linearity, we highlight four properties of macroscopic neurodynamics which can counteract or mask microscopic nonlinear dynamics: averaging over space, averaging over time, observation noise, and limited data samples. Whereas the latter two are technological limitations and can improve in the future, the former two are inherent to aggregated macroscopic brain activity. Our results, together with the unparalleled interpretability of linear models, can greatly facilitate our understanding of macroscopic neural dynamics and the principled design of model-based interventions for the treatment of neuropsychiatric disorders.

Improving J-divergence of brain connectivity states by graph Laplacian denoising

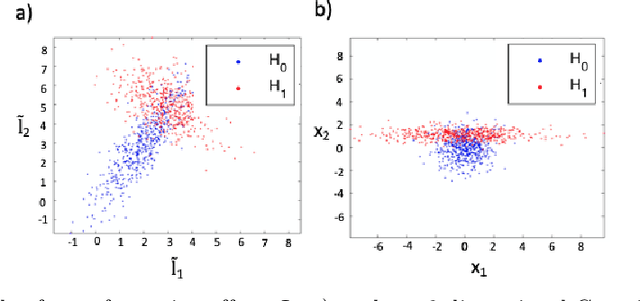
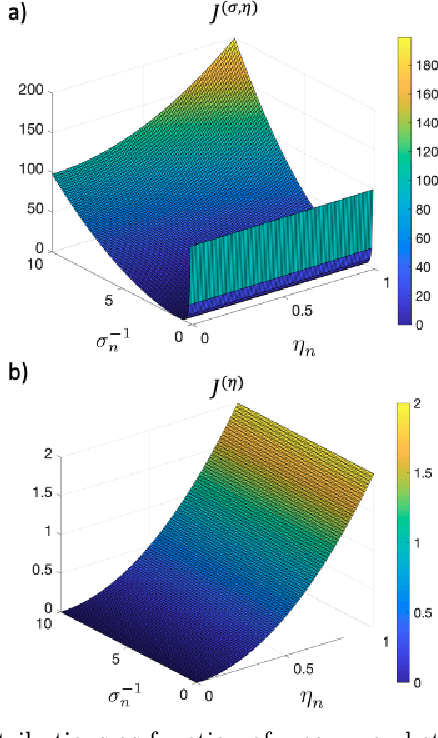
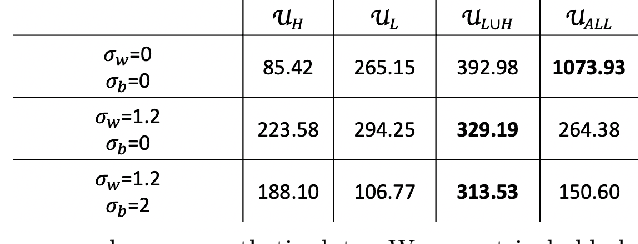
Functional connectivity (FC) can be represented as a network, and is frequently used to better understand the neural underpinnings of complex tasks such as motor imagery (MI) detection in brain-computer interfaces (BCIs). However, errors in the estimation of connectivity can affect the detection performances. In this work, we address the problem of denoising common connectivity estimates to improve the detectability of different connectivity states. Specifically, we propose a denoising algorithm that acts on the network graph Laplacian, which leverages recent graph signal processing results. Further, we derive a novel formulation of the Jensen divergence for the denoised Laplacian under different states. Numerical simulations on synthetic data show that the denoising method improves the Jensen divergence of connectivity patterns corresponding to different task conditions. Furthermore, we apply the Laplacian denoising technique to brain networks estimated from real EEG data recorded during MI-BCI experiments. Using our novel formulation of the J-divergence, we are able to quantify the distance between the FC networks in the motor imagery and resting states, as well as to understand the contribution of each Laplacian variable to the total J-divergence between two states. Experimental results on real MI-BCI EEG data demonstrate that the Laplacian denoising improves the separation of motor imagery and resting mental states, and shortens the time interval required for connectivity estimation. We conclude that the approach shows promise for the robust detection of connectivity states while being appealing for implementation in real-time BCI applications.

The growth and form of knowledge networks by kinesthetic curiosity

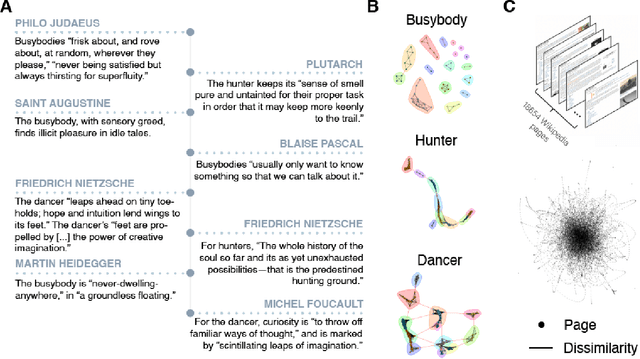
Throughout life, we might seek a calling, companions, skills, entertainment, truth, self-knowledge, beauty, and edification. The practice of curiosity can be viewed as an extended and open-ended search for valuable information with hidden identity and location in a complex space of interconnected information. Despite its importance, curiosity has been challenging to computationally model because the practice of curiosity often flourishes without specific goals, external reward, or immediate feedback. Here, we show how network science, statistical physics, and philosophy can be integrated into an approach that coheres with and expands the psychological taxonomies of specific-diversive and perceptual-epistemic curiosity. Using this interdisciplinary approach, we distill functional modes of curious information seeking as searching movements in information space. The kinesthetic model of curiosity offers a vibrant counterpart to the deliberative predictions of model-based reinforcement learning. In doing so, this model unearths new computational opportunities for identifying what makes curiosity curious.

Teaching Recurrent Neural Networks to Modify Chaotic Memories by Example

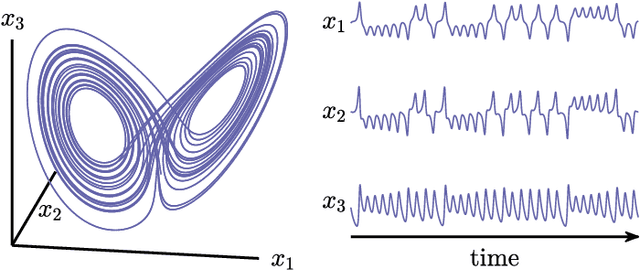
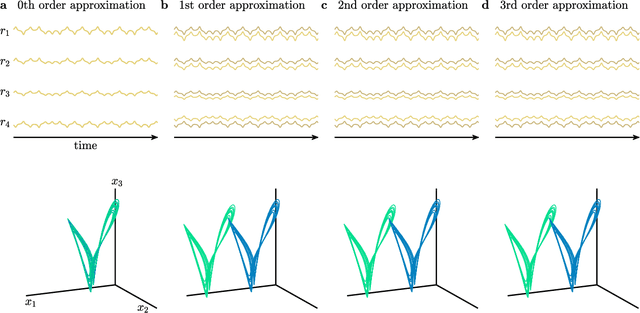
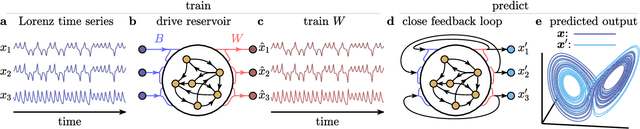
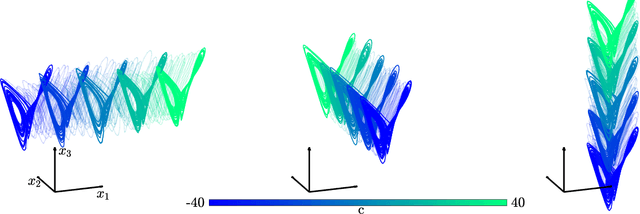
The ability to store and manipulate information is a hallmark of computational systems. Whereas computers are carefully engineered to represent and perform mathematical operations on structured data, neurobiological systems perform analogous functions despite flexible organization and unstructured sensory input. Recent efforts have made progress in modeling the representation and recall of information in neural systems. However, precisely how neural systems learn to modify these representations remains far from understood. Here we demonstrate that a recurrent neural network (RNN) can learn to modify its representation of complex information using only examples, and we explain the associated learning mechanism with new theory. Specifically, we drive an RNN with examples of translated, linearly transformed, or pre-bifurcated time series from a chaotic Lorenz system, alongside an additional control signal that changes value for each example. By training the network to replicate the Lorenz inputs, it learns to autonomously evolve about a Lorenz-shaped manifold. Additionally, it learns to continuously interpolate and extrapolate the translation, transformation, and bifurcation of this representation far beyond the training data by changing the control signal. Finally, we provide a mechanism for how these computations are learned, and demonstrate that a single network can simultaneously learn multiple computations. Together, our results provide a simple but powerful mechanism by which an RNN can learn to manipulate internal representations of complex information, allowing for the principled study and precise design of RNNs.

Architecture and evolution of semantic networks in mathematics texts

Knowledge is a network of interconnected concepts. Yet, precisely how the topological structure of knowledge constrains its acquisition remains unknown, hampering the development of learning enhancement strategies. Here we study the topological structure of semantic networks reflecting mathematical concepts and their relations in college-level linear algebra texts. We hypothesize that these networks will exhibit structural order, reflecting the logical sequence of topics that ensures accessibility. We find that the networks exhibit strong core-periphery architecture, where a dense core of concepts presented early is complemented with a sparse periphery presented evenly throughout the exposition; the latter is composed of many small modules each reflecting more narrow domains. Using tools from applied topology, we find that the expositional evolution of the semantic networks produces and subsequently fills knowledge gaps, and that the density of these gaps tracks negatively with community ratings of each textbook. Broadly, our study lays the groundwork for future efforts developing optimal design principles for textbook exposition and teaching in a classroom setting.

Finding the needle in high-dimensional haystack: A tutorial on canonical correlation analysis

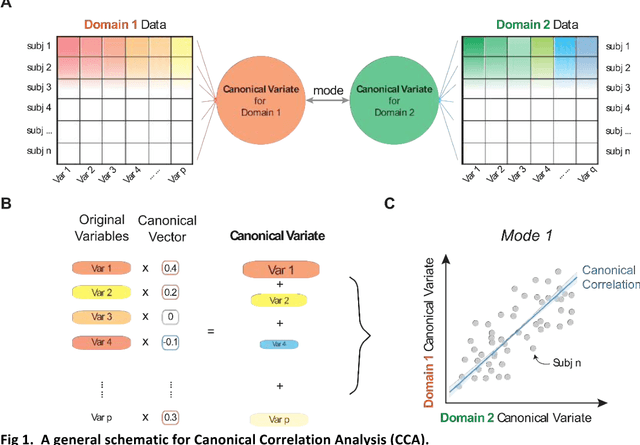
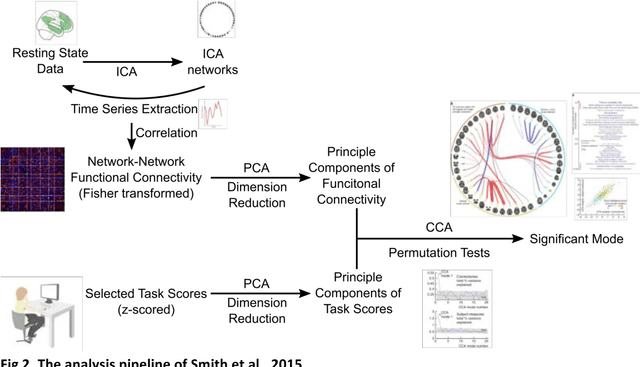
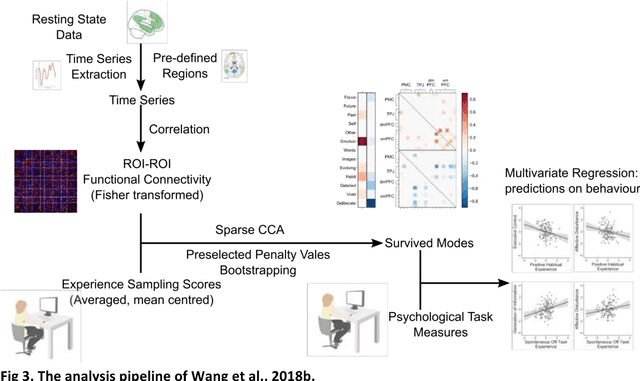
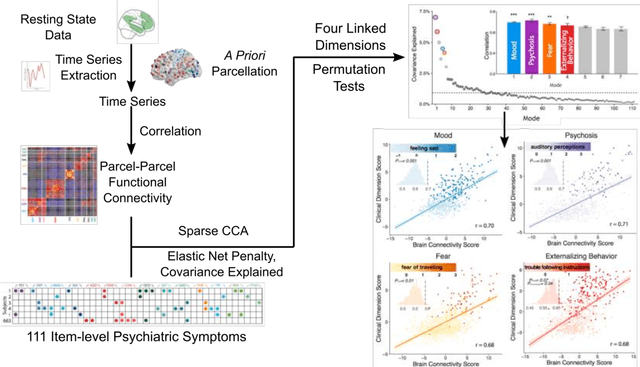
Since the beginning of the 21st century, the size, breadth, and granularity of data in biology and medicine has grown rapidly. In the example of neuroscience, studies with thousands of subjects are becoming more common, which provide extensive phenotyping on the behavioral, neural, and genomic level with hundreds of variables. The complexity of such big data repositories offer new opportunities and pose new challenges to investigate brain, cognition, and disease. Canonical correlation analysis (CCA) is a prototypical family of methods for wrestling with and harvesting insight from such rich datasets. This doubly-multivariate tool can simultaneously consider two variable sets from different modalities to uncover essential hidden associations. Our primer discusses the rationale, promises, and pitfalls of CCA in biomedicine.