Is the brain macroscopically linear? A system identification of resting state dynamics

A central challenge in the computational modeling of neural dynamics is the trade-off between accuracy and simplicity. At the level of individual neurons, nonlinear dynamics are both experimentally established and essential for neuronal functioning. An implicit assumption has thus formed that an accurate computational model of whole-brain dynamics must also be highly nonlinear, whereas linear models may provide a first-order approximation. Here, we provide a rigorous and data-driven investigation of this hypothesis at the level of whole-brain blood-oxygen-level-dependent (BOLD) and macroscopic field potential dynamics by leveraging the theory of system identification. Using functional MRI (fMRI) and intracranial EEG (iEEG), we model the resting state activity of 700 subjects in the Human Connectome Project (HCP) and 122 subjects from the Restoring Active Memory (RAM) project using state-of-the-art linear and nonlinear model families. We assess relative model fit using predictive power, computational complexity, and the extent of residual dynamics unexplained by the model. Contrary to our expectations, linear auto-regressive models achieve the best measures across all three metrics, eliminating the trade-off between accuracy and simplicity. To understand and explain this linearity, we highlight four properties of macroscopic neurodynamics which can counteract or mask microscopic nonlinear dynamics: averaging over space, averaging over time, observation noise, and limited data samples. Whereas the latter two are technological limitations and can improve in the future, the former two are inherent to aggregated macroscopic brain activity. Our results, together with the unparalleled interpretability of linear models, can greatly facilitate our understanding of macroscopic neural dynamics and the principled design of model-based interventions for the treatment of neuropsychiatric disorders.

Teaching Recurrent Neural Networks to Modify Chaotic Memories by Example

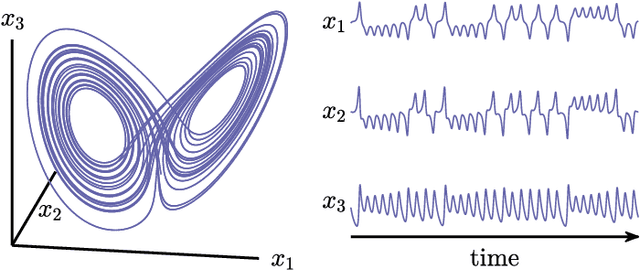
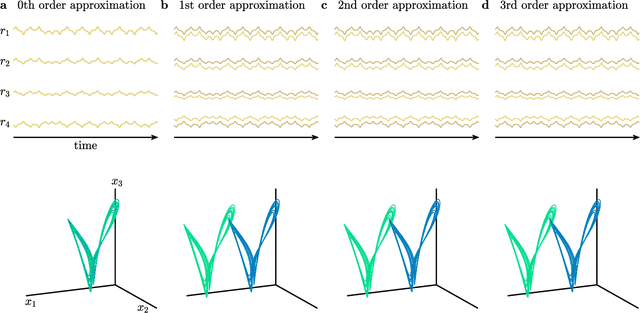
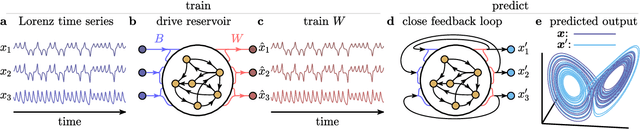
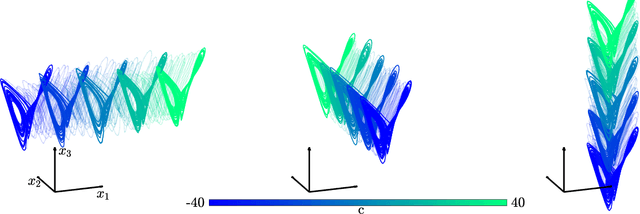
The ability to store and manipulate information is a hallmark of computational systems. Whereas computers are carefully engineered to represent and perform mathematical operations on structured data, neurobiological systems perform analogous functions despite flexible organization and unstructured sensory input. Recent efforts have made progress in modeling the representation and recall of information in neural systems. However, precisely how neural systems learn to modify these representations remains far from understood. Here we demonstrate that a recurrent neural network (RNN) can learn to modify its representation of complex information using only examples, and we explain the associated learning mechanism with new theory. Specifically, we drive an RNN with examples of translated, linearly transformed, or pre-bifurcated time series from a chaotic Lorenz system, alongside an additional control signal that changes value for each example. By training the network to replicate the Lorenz inputs, it learns to autonomously evolve about a Lorenz-shaped manifold. Additionally, it learns to continuously interpolate and extrapolate the translation, transformation, and bifurcation of this representation far beyond the training data by changing the control signal. Finally, we provide a mechanism for how these computations are learned, and demonstrate that a single network can simultaneously learn multiple computations. Together, our results provide a simple but powerful mechanism by which an RNN can learn to manipulate internal representations of complex information, allowing for the principled study and precise design of RNNs.

Hierarchical Selective Recruitment in Linear-Threshold Brain Networks - Part I: Intra-Layer Dynamics and Selective Inhibition

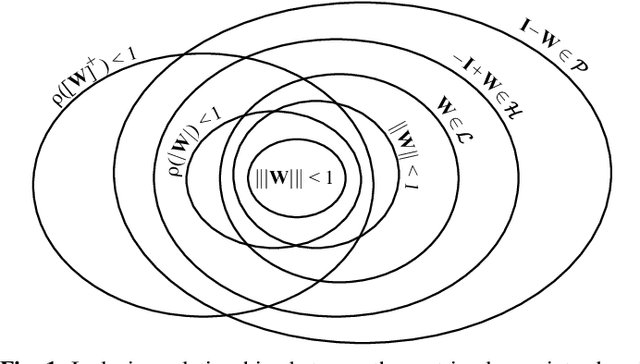
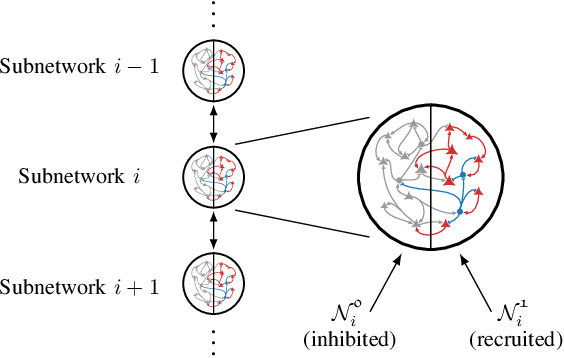
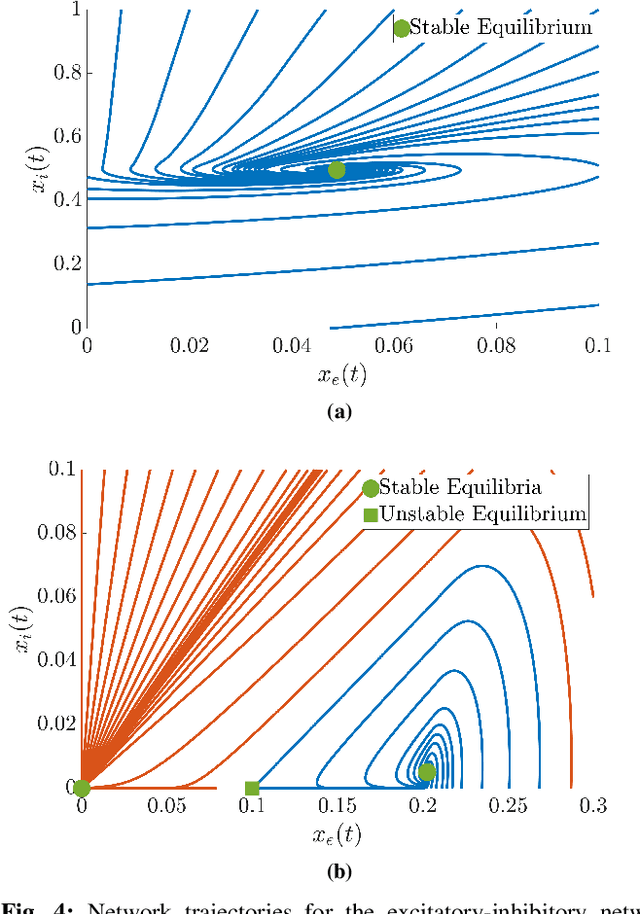
Goal-driven selective attention (GDSA) refers to the brain's function of prioritizing, according to one's internal goals and desires, the activity of a task-relevant subset of its overall network to efficiently process relevant information while inhibiting the effects of distractions. Despite decades of research in neuroscience, a comprehensive understanding of GDSA is still lacking. We propose a novel framework for GDSA using concepts and tools from control theory as well as insights and structures from neuroscience. Central to this framework is an information-processing hierarchy with two main components: selective inhibition of task-irrelevant activity and top-down recruitment of task-relevant activity. We analyze the internal dynamics of each layer of the hierarchy described as a network with linear-threshold dynamics and derive conditions on its structure to guarantee existence and uniqueness of equilibria, asymptotic stability, and boundedness of trajectories. We also provide mechanisms that enforce selective inhibition using the biologically-inspired schemes of feedforward and feedback inhibition. Despite their differences, both schemes lead to the same conclusion: the intrinsic dynamical properties of the (not-inhibited) task-relevant subnetworks are the sole determiner of the dynamical properties that are achievable under selective inhibition.

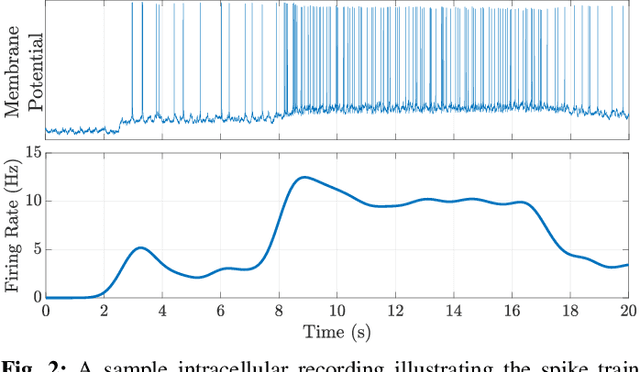
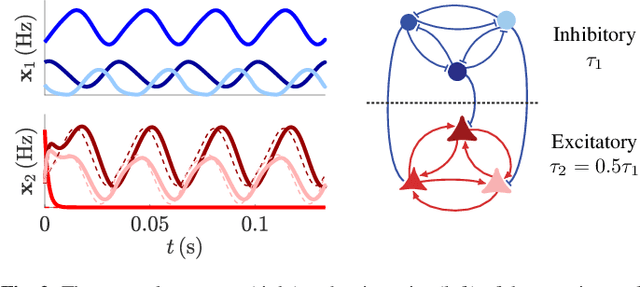
Hierarchical Selective Recruitment in Linear-Threshold Brain Networks - Part II: Inter-Layer Dynamics and Top-Down Recruitment

Goal-driven selective attention (GDSA) is a remarkable function that allows the complex dynamical networks of the brain to support coherent perception and cognition. Part I of this two-part paper proposes a new control-theoretic framework, termed hierarchical selective recruitment (HSR), to rigorously explain the emergence of GDSA from the brain's network structure and dynamics. This part completes the development of HSR by deriving conditions on the joint structure of the hierarchical subnetworks that guarantee top-down recruitment of the task-relevant part of each subnetwork by the subnetwork at the layer immediately above, while inhibiting the activity of task-irrelevant subnetworks at all the hierarchical layers. To further verify the merit and applicability of this framework, we carry out a comprehensive case study of selective listening in rodents and show that a small network with HSR-based structure and minimal size can explain the data with remarkable accuracy while satisfying the theoretical requirements of HSR. Our technical approach relies on the theory of switched systems and provides a novel converse Lyapunov theorem for state-dependent switched affine systems that is of independent interest.