Certifying Stability of Reinforcement Learning Policies using Generalized Lyapunov Functions

We study the problem of certifying the stability of closed-loop systems under control policies derived from optimal control or reinforcement learning (RL). Classical Lyapunov methods require a strict step-wise decrease in the Lyapunov function but such a certificate is difficult to construct for a learned control policy. The value function associated with an RL policy is a natural Lyapunov function candidate but it is not clear how it should be modified. To gain intuition, we first study the linear quadratic regulator (LQR) problem and make two key observations. First, a Lyapunov function can be obtained from the value function of an LQR policy by augmenting it with a residual term related to the system dynamics and stage cost. Second, the classical Lyapunov decrease requirement can be relaxed to a generalized Lyapunov condition requiring only decrease on average over multiple time steps. Using this intuition, we consider the nonlinear setting and formulate an approach to learn generalized Lyapunov functions by augmenting RL value functions with neural network residual terms. Our approach successfully certifies the stability of RL policies trained on Gymnasium and DeepMind Control benchmarks. We also extend our method to jointly train neural controllers and stability certificates using a multi-step Lyapunov loss, resulting in larger certified inner approximations of the region of attraction compared to the classical Lyapunov approach. Overall, our formulation enables stability certification for a broad class of systems with learned policies by making certificates easier to construct, thereby bridging classical control theory and modern learning-based methods.

Variational Formulation of the Particle Flow Particle Filter

This paper provides a formulation of the particle flow particle filter from the perspective of variational inference. We show that the transient density used to derive the particle flow particle filter follows a time-scaled trajectory of the Fisher-Rao gradient flow in the space of probability densities. The Fisher-Rao gradient flow is obtained as a continuous-time algorithm for variational inference, minimizing the Kullback-Leibler divergence between a variational density and the true posterior density.

Back to Base: Towards Hands-Off Learning via Safe Resets with Reach-Avoid Safety Filters

Designing controllers that accomplish tasks while guaranteeing safety constraints remains a significant challenge. We often want an agent to perform well in a nominal task, such as environment exploration, while ensuring it can avoid unsafe states and return to a desired target by a specific time. In particular we are motivated by the setting of safe, efficient, hands-off training for reinforcement learning in the real world. By enabling a robot to safely and autonomously reset to a desired region (e.g., charging stations) without human intervention, we can enhance efficiency and facilitate training. Safety filters, such as those based on control barrier functions, decouple safety from nominal control objectives and rigorously guarantee safety. Despite their success, constructing these functions for general nonlinear systems with control constraints and system uncertainties remains an open problem. This paper introduces a safety filter obtained from the value function associated with the reach-avoid problem. The proposed safety filter minimally modifies the nominal controller while avoiding unsafe regions and guiding the system back to the desired target set. By preserving policy performance while allowing safe resetting, we enable efficient hands-off reinforcement learning and advance the feasibility of safe training for real world robots. We demonstrate our approach using a modified version of soft actor-critic to safely train a swing-up task on a modified cartpole stabilization problem.

Safe and Dynamically-Feasible Motion Planning using Control Lyapunov and Barrier Functions

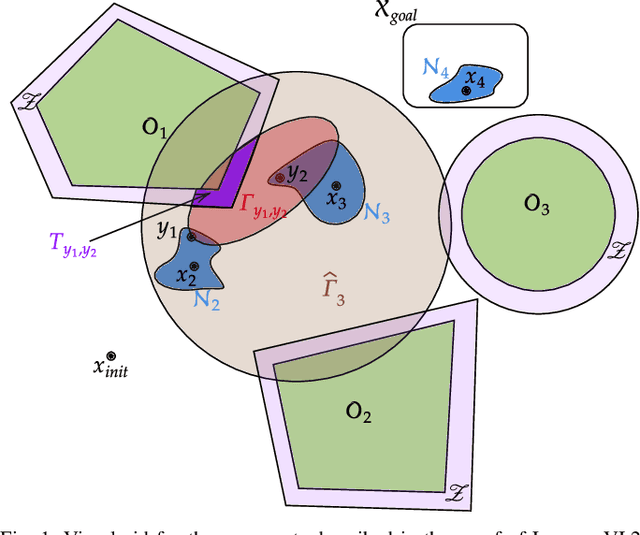
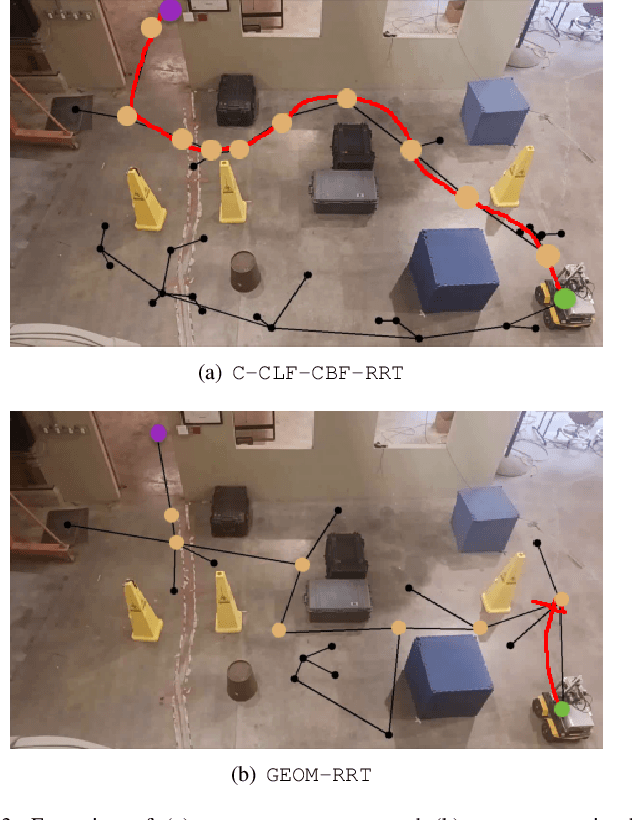
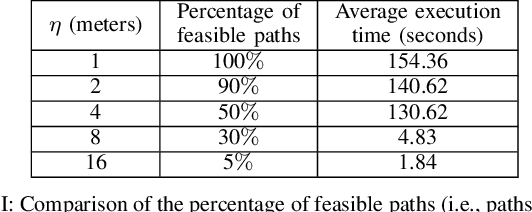
This paper considers the problem of designing motion planning algorithms for control-affine systems that generate collision-free paths from an initial to a final destination and can be executed using safe and dynamically-feasible controllers. We introduce the C-CLF-CBF-RRT algorithm, which produces paths with such properties and leverages rapidly exploring random trees (RRTs), control Lyapunov functions (CLFs) and control barrier functions (CBFs). We show that C-CLF-CBF-RRT is computationally efficient for a variety of different dynamics and obstacles, and establish its probabilistic completeness. We showcase the performance of C-CLF-CBF-RRT in different simulation and hardware experiments.

Online Event-Triggered Switching for Frequency Control in Power Grids with Variable Inertia

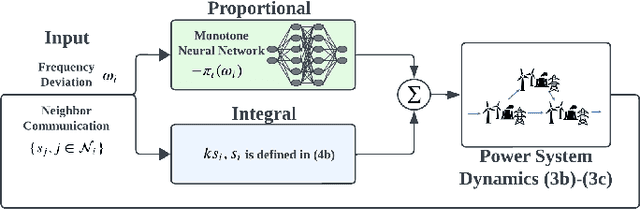
The increasing integration of renewable energy resources into power grids has led to time-varying system inertia and consequent degradation in frequency dynamics. A promising solution to alleviate performance degradation is using power electronics interfaced energy resources, such as renewable generators and battery energy storage for primary frequency control, by adjusting their power output set-points in response to frequency deviations. However, designing a frequency controller under time-varying inertia is challenging. Specifically, the stability or optimality of controllers designed for time-invariant systems can be compromised once applied to a time-varying system. We model the frequency dynamics under time-varying inertia as a nonlinear switching system, where the frequency dynamics under each mode are described by the nonlinear swing equations and different modes represent different inertia levels. We identify a key controller structure, named Neural Proportional-Integral (Neural-PI) controller, that guarantees exponential input-to-state stability for each mode. To further improve performance, we present an online event-triggered switching algorithm to select the most suitable controller from a set of Neural-PI controllers, each optimized for specific inertia levels. Simulations on the IEEE 39-bus system validate the effectiveness of the proposed online switching control method with stability guarantees and optimized performance for frequency control under time-varying inertia.

Sensor-Based Distributionally Robust Control for Safe Robot Navigation in Dynamic Environments

We introduce a novel method for safe mobile robot navigation in dynamic, unknown environments, utilizing onboard sensing to impose safety constraints without the need for accurate map reconstruction. Traditional methods typically rely on detailed map information to synthesize safe stabilizing controls for mobile robots, which can be computationally demanding and less effective, particularly in dynamic operational conditions. By leveraging recent advances in distributionally robust optimization, we develop a distributionally robust control barrier function (DR-CBF) constraint that directly processes range sensor data to impose safety constraints. Coupling this with a control Lyapunov function (CLF) for path tracking, we demonstrate that our CLF-DR-CBF control synthesis method achieves safe, efficient, and robust navigation in uncertain dynamic environments. We demonstrate the effectiveness of our approach in simulated and real autonomous robot navigation experiments, marking a substantial advancement in real-time safety guarantees for mobile robots.

Designing Poisson Integrators Through Machine Learning

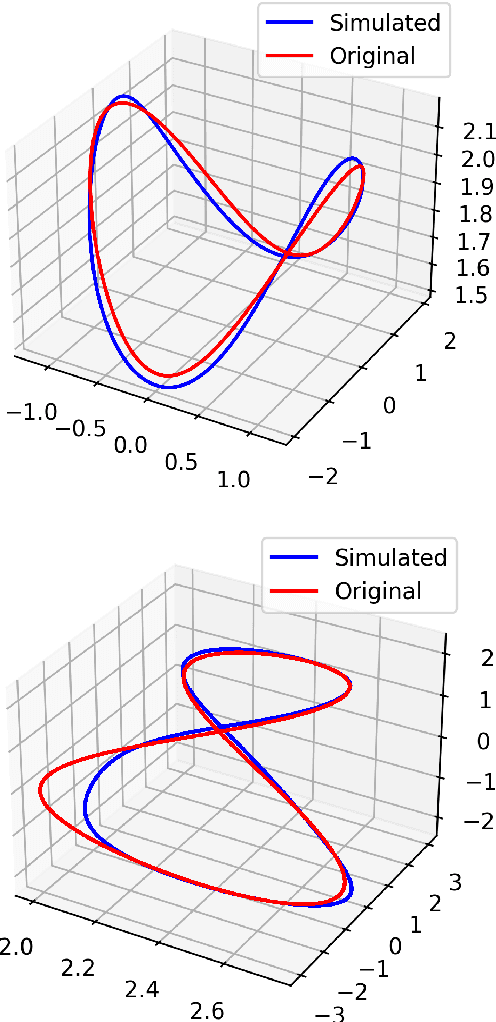
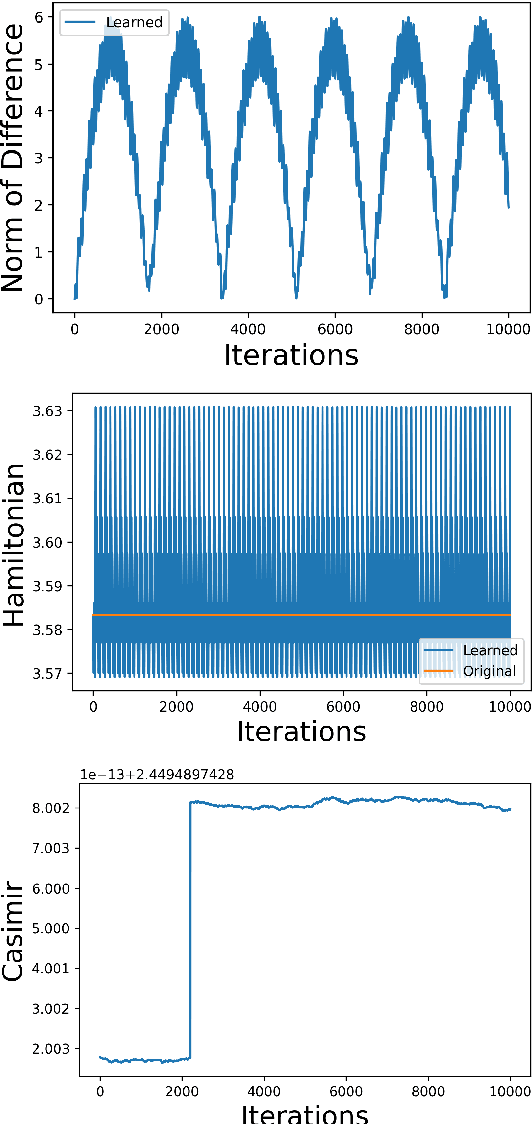
This paper presents a general method to construct Poisson integrators, i.e., integrators that preserve the underlying Poisson geometry. We assume the Poisson manifold is integrable, meaning there is a known local symplectic groupoid for which the Poisson manifold serves as the set of units. Our constructions build upon the correspondence between Poisson diffeomorphisms and Lagrangian bisections, which allows us to reformulate the design of Poisson integrators as solutions to a certain PDE (Hamilton-Jacobi). The main novelty of this work is to understand the Hamilton-Jacobi PDE as an optimization problem, whose solution can be easily approximated using machine learning related techniques. This research direction aligns with the current trend in the PDE and machine learning communities, as initiated by Physics- Informed Neural Networks, advocating for designs that combine both physical modeling (the Hamilton-Jacobi PDE) and data.

Symmetry Preservation in Hamiltonian Systems: Simulation and Learning

This work presents a general geometric framework for simulating and learning the dynamics of Hamiltonian systems that are invariant under a Lie group of transformations. This means that a group of symmetries is known to act on the system respecting its dynamics and, as a consequence, Noether's Theorem, conserved quantities are observed. We propose to simulate and learn the mappings of interest through the construction of $G$-invariant Lagrangian submanifolds, which are pivotal objects in symplectic geometry. A notable property of our constructions is that the simulated/learned dynamics also preserves the same conserved quantities as the original system, resulting in a more faithful surrogate of the original dynamics than non-symmetry aware methods, and in a more accurate predictor of non-observed trajectories. Furthermore, our setting is able to simulate/learn not only Hamiltonian flows, but any Lie group-equivariant symplectic transformation. Our designs leverage pivotal techniques and concepts in symplectic geometry and geometric mechanics: reduction theory, Noether's Theorem, Lagrangian submanifolds, momentum mappings, and coisotropic reduction among others. We also present methods to learn Poisson transformations while preserving the underlying geometry and how to endow non-geometric integrators with geometric properties. Thus, this work presents a novel attempt to harness the power of symplectic and Poisson geometry towards simulating and learning problems.

Temporal Forward-Backward Consistency, Not Residual Error, Measures the Prediction Accuracy of Extended Dynamic Mode Decomposition

Extended Dynamic Mode Decomposition (EDMD) is a popular data-driven method to approximate the action of the Koopman operator on a linear function space spanned by a dictionary of functions. The accuracy of EDMD model critically depends on the quality of the particular dictionary's span, specifically on how close it is to being invariant under the Koopman operator. Motivated by the observation that the residual error of EDMD, typically used for dictionary learning, does not encode the quality of the function space and is sensitive to the choice of basis, we introduce the novel concept of consistency index. We show that this measure, based on using EDMD forward and backward in time, enjoys a number of desirable qualities that make it suitable for data-driven modeling of dynamical systems: it measures the quality of the function space, it is invariant under the choice of basis, can be computed in closed form from the data, and provides a tight upper-bound for the relative root mean square error of all function predictions on the entire span of the dictionary.

Safe Control Synthesis with Uncertain Dynamics and Constraints

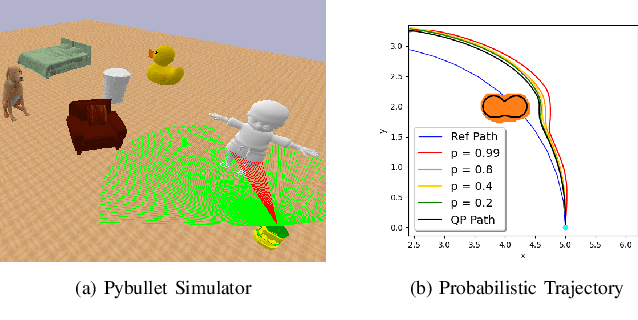
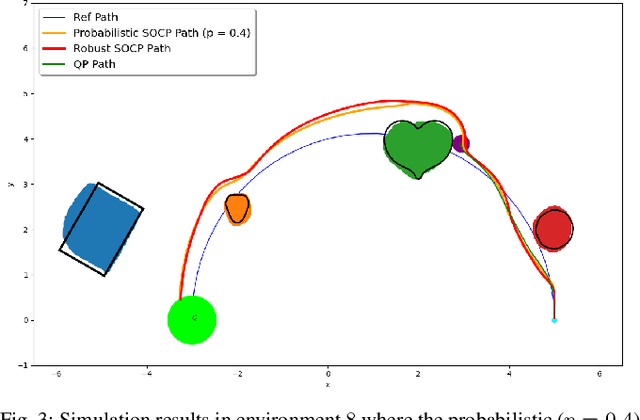
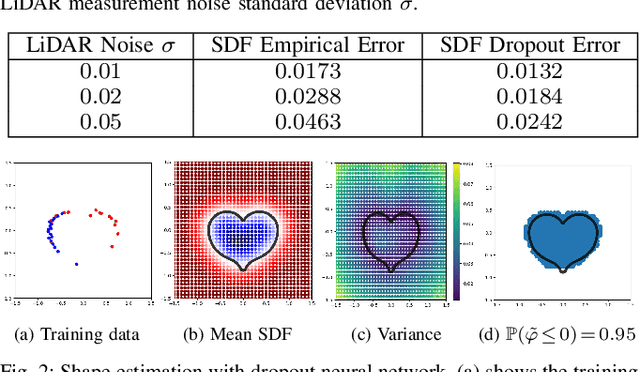
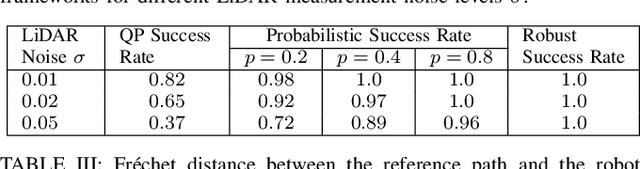
This paper considers safe control synthesis for dynamical systems in the presence of uncertainty in the dynamics model and the safety constraints that the system must satisfy. Our approach captures probabilistic and worst-case model errors and their effect on control Lyapunov function (CLF) and control barrier function (CBF) constraints in the control-synthesis optimization problem. We show that both the probabilistic and robust formulations lead to second-order cone programs (SOCPs), enabling safe and stable control synthesis that can be performed efficiently online. We evaluate our approach in PyBullet simulations of an autonomous robot navigating in unknown environments and compare the performance with a baseline CLF-CBF quadratic programming approach.