Momentum-based gradient descent methods for Lie groups

Polyak's Heavy Ball (PHB; Polyak, 1964), a.k.a. Classical Momentum, and Nesterov's Accelerated Gradient (NAG; Nesterov, 1983) are well know examples of momentum-descent methods for optimization. While the latter outperforms the former, solely generalizations of PHB-like methods to nonlinear spaces have been described in the literature. We propose here a generalization of NAG-like methods for Lie group optimization based on the variational one-to-one correspondence between classical and accelerated momentum methods (Campos et al., 2023). Numerical experiments are shown.

Designing Poisson Integrators Through Machine Learning

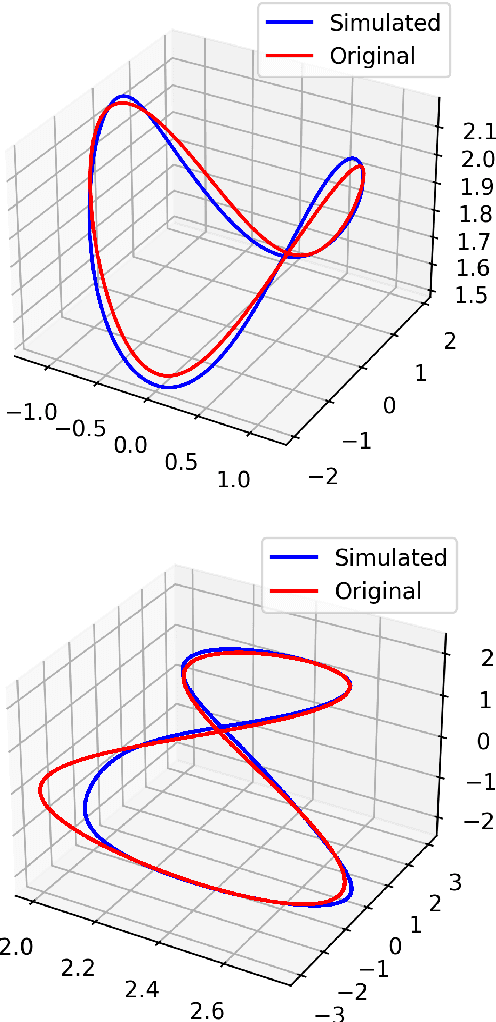
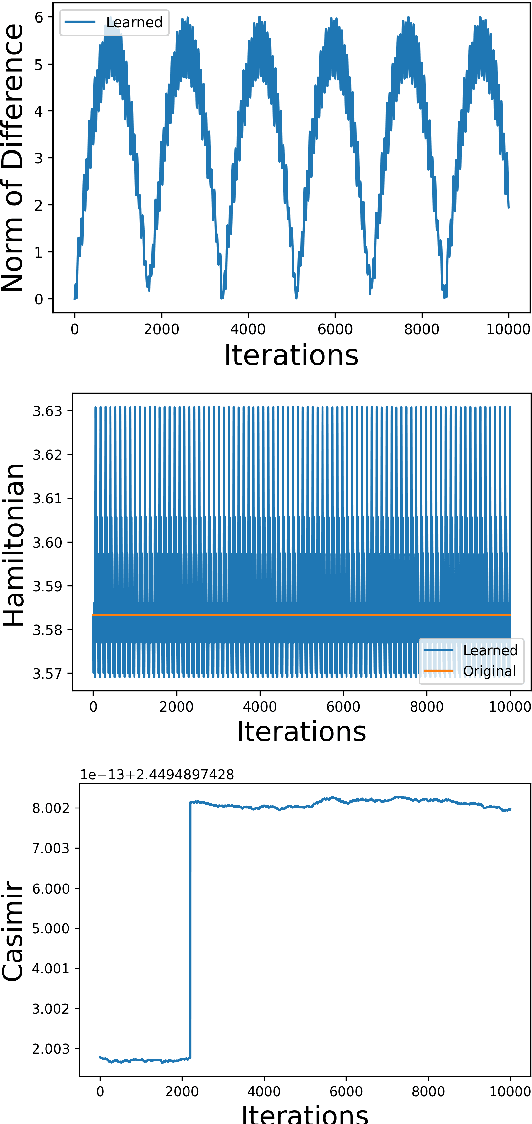
This paper presents a general method to construct Poisson integrators, i.e., integrators that preserve the underlying Poisson geometry. We assume the Poisson manifold is integrable, meaning there is a known local symplectic groupoid for which the Poisson manifold serves as the set of units. Our constructions build upon the correspondence between Poisson diffeomorphisms and Lagrangian bisections, which allows us to reformulate the design of Poisson integrators as solutions to a certain PDE (Hamilton-Jacobi). The main novelty of this work is to understand the Hamilton-Jacobi PDE as an optimization problem, whose solution can be easily approximated using machine learning related techniques. This research direction aligns with the current trend in the PDE and machine learning communities, as initiated by Physics- Informed Neural Networks, advocating for designs that combine both physical modeling (the Hamilton-Jacobi PDE) and data.

Symmetry Preservation in Hamiltonian Systems: Simulation and Learning

This work presents a general geometric framework for simulating and learning the dynamics of Hamiltonian systems that are invariant under a Lie group of transformations. This means that a group of symmetries is known to act on the system respecting its dynamics and, as a consequence, Noether's Theorem, conserved quantities are observed. We propose to simulate and learn the mappings of interest through the construction of $G$-invariant Lagrangian submanifolds, which are pivotal objects in symplectic geometry. A notable property of our constructions is that the simulated/learned dynamics also preserves the same conserved quantities as the original system, resulting in a more faithful surrogate of the original dynamics than non-symmetry aware methods, and in a more accurate predictor of non-observed trajectories. Furthermore, our setting is able to simulate/learn not only Hamiltonian flows, but any Lie group-equivariant symplectic transformation. Our designs leverage pivotal techniques and concepts in symplectic geometry and geometric mechanics: reduction theory, Noether's Theorem, Lagrangian submanifolds, momentum mappings, and coisotropic reduction among others. We also present methods to learn Poisson transformations while preserving the underlying geometry and how to endow non-geometric integrators with geometric properties. Thus, this work presents a novel attempt to harness the power of symplectic and Poisson geometry towards simulating and learning problems.

A Discrete Variational Derivation of Accelerated Methods in Optimization

Many of the new developments in machine learning are connected with gradient-based optimization methods. Recently, these methods have been studied using a variational perspective. This has opened up the possibility of introducing variational and symplectic integration methods using geometric integrators. In particular, in this paper, we introduce variational integrators which allow us to derive different methods for optimization. Using both, Hamilton's principle and Lagrange-d'Alembert's, we derive two families of optimization methods in one-to-one correspondence that generalize Polyak's heavy ball and the well known Nesterov accelerated gradient method, mimicking the behavior of the latter which reduces the oscillations of typical momentum methods. However, since the systems considered are explicitly time-dependent, the preservation of symplecticity of autonomous systems occurs here solely on the fibers. Several experiments exemplify the result.

On the observability of relative positions in left-invariant multi-agent control systems and its application to formation control

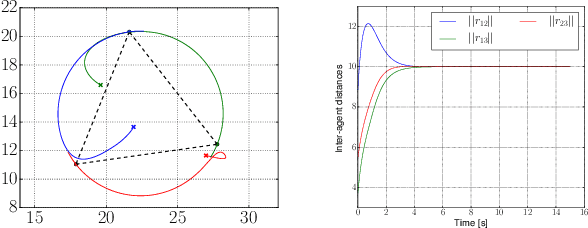
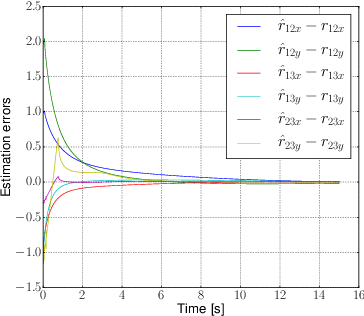
We consider the localization problem between agents while they run a formation control algorithm. These algorithms typically demand from the agents the information about their relative positions with respect to their neighbors. We assume that this information is not available. Therefore, the agents need to solve the observability problem of reconstructing their relative positions based on other measurements between them. We first model the relative kinematics between the agents as a left-invariant control system so that we can exploit its appealing properties to solve the observability problem. Then, as a particular application, we will focus on agents running a distance-based control algorithm where their relative positions are not accessible but the distances between them are.