Designing Poisson Integrators Through Machine Learning

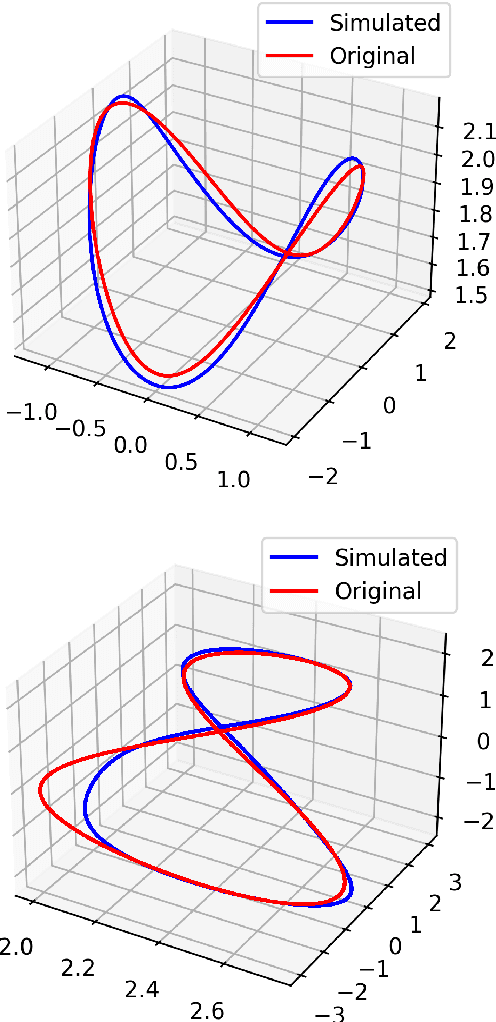
This paper presents a general method to construct Poisson integrators, i.e., integrators that preserve the underlying Poisson geometry. We assume the Poisson manifold is integrable, meaning there is a known local symplectic groupoid for which the Poisson manifold serves as the set of units. Our constructions build upon the correspondence between Poisson diffeomorphisms and Lagrangian bisections, which allows us to reformulate the design of Poisson integrators as solutions to a certain PDE (Hamilton-Jacobi). The main novelty of this work is to understand the Hamilton-Jacobi PDE as an optimization problem, whose solution can be easily approximated using machine learning related techniques. This research direction aligns with the current trend in the PDE and machine learning communities, as initiated by Physics- Informed Neural Networks, advocating for designs that combine both physical modeling (the Hamilton-Jacobi PDE) and data.

Symmetry Preservation in Hamiltonian Systems: Simulation and Learning

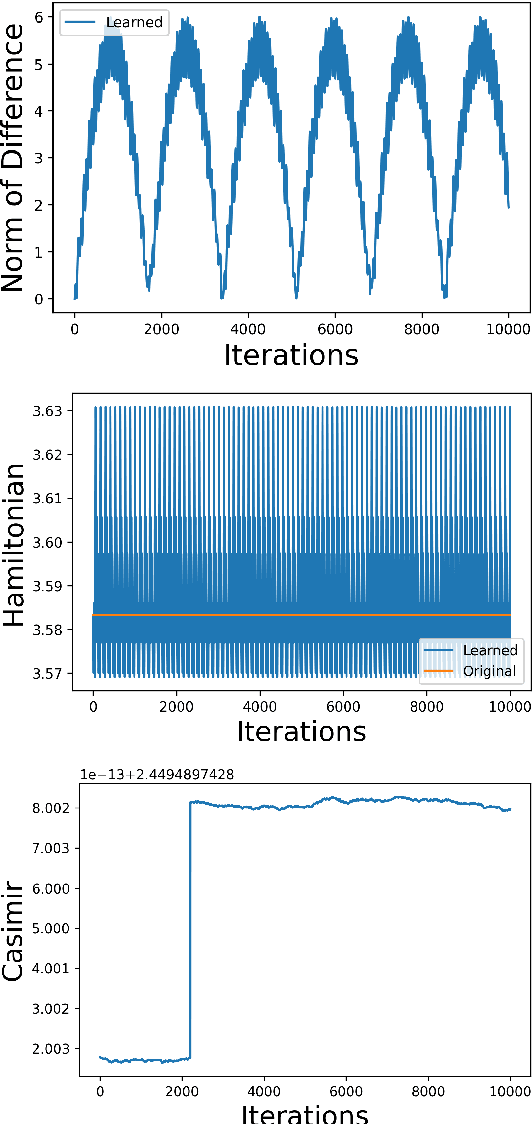
This work presents a general geometric framework for simulating and learning the dynamics of Hamiltonian systems that are invariant under a Lie group of transformations. This means that a group of symmetries is known to act on the system respecting its dynamics and, as a consequence, Noether's Theorem, conserved quantities are observed. We propose to simulate and learn the mappings of interest through the construction of $G$-invariant Lagrangian submanifolds, which are pivotal objects in symplectic geometry. A notable property of our constructions is that the simulated/learned dynamics also preserves the same conserved quantities as the original system, resulting in a more faithful surrogate of the original dynamics than non-symmetry aware methods, and in a more accurate predictor of non-observed trajectories. Furthermore, our setting is able to simulate/learn not only Hamiltonian flows, but any Lie group-equivariant symplectic transformation. Our designs leverage pivotal techniques and concepts in symplectic geometry and geometric mechanics: reduction theory, Noether's Theorem, Lagrangian submanifolds, momentum mappings, and coisotropic reduction among others. We also present methods to learn Poisson transformations while preserving the underlying geometry and how to endow non-geometric integrators with geometric properties. Thus, this work presents a novel attempt to harness the power of symplectic and Poisson geometry towards simulating and learning problems.