Neural Configuration-Space Barriers for Manipulation Planning and Control

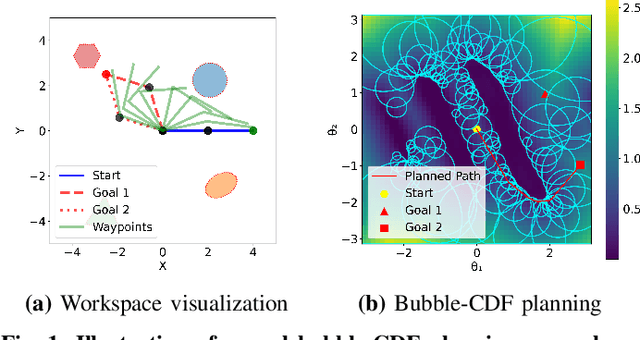
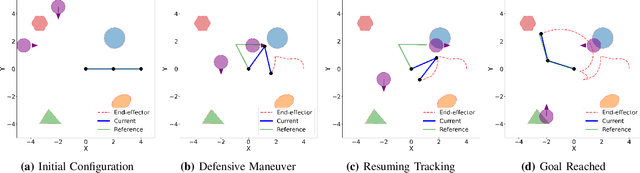
Planning and control for high-dimensional robot manipulators in cluttered, dynamic environments require both computational efficiency and robust safety guarantees. Inspired by recent advances in learning configuration-space distance functions (CDFs) as robot body representations, we propose a unified framework for motion planning and control that formulates safety constraints as CDF barriers. A CDF barrier approximates the local free configuration space, substantially reducing the number of collision-checking operations during motion planning. However, learning a CDF barrier with a neural network and relying on online sensor observations introduce uncertainties that must be considered during control synthesis. To address this, we develop a distributionally robust CDF barrier formulation for control that explicitly accounts for modeling errors and sensor noise without assuming a known underlying distribution. Simulations and hardware experiments on a 6-DoF xArm manipulator show that our neural CDF barrier formulation enables efficient planning and robust real-time safe control in cluttered and dynamic environments, relying only on onboard point-cloud observations.

Learning Generalized Hamiltonians using fully Symplectic Mappings

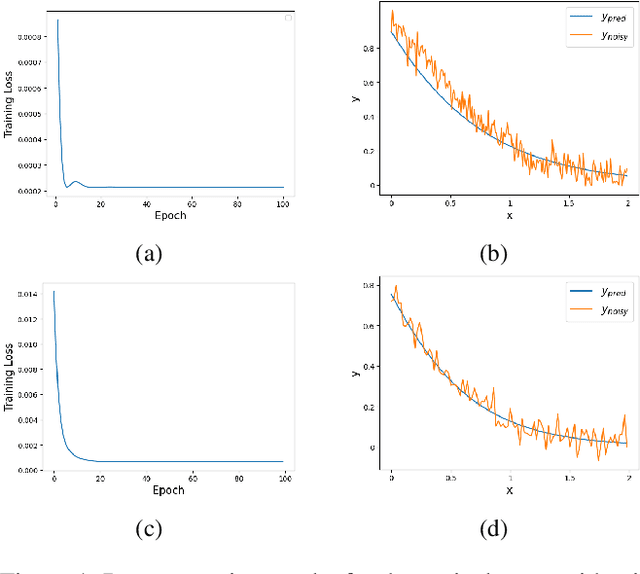
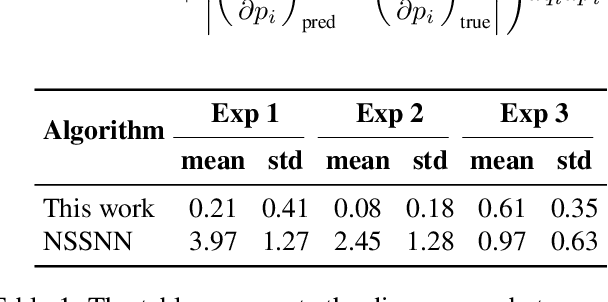
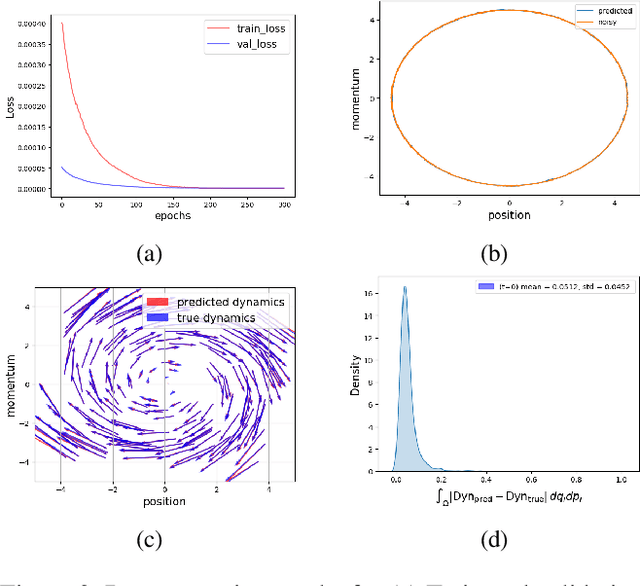
Many important physical systems can be described as the evolution of a Hamiltonian system, which has the important property of being conservative, that is, energy is conserved throughout the evolution. Physics Informed Neural Networks and in particular Hamiltonian Neural Networks have emerged as a mechanism to incorporate structural inductive bias into the NN model. By ensuring physical invariances are conserved, the models exhibit significantly better sample complexity and out-of-distribution accuracy than standard NNs. Learning the Hamiltonian as a function of its canonical variables, typically position and velocity, from sample observations of the system thus becomes a critical task in system identification and long-term prediction of system behavior. However, to truly preserve the long-run physical conservation properties of Hamiltonian systems, one must use symplectic integrators for a forward pass of the system's simulation. While symplectic schemes have been used in the literature, they are thus far limited to situations when they reduce to explicit algorithms, which include the case of separable Hamiltonians or augmented non-separable Hamiltonians. We extend it to generalized non-separable Hamiltonians, and noting the self-adjoint property of symplectic integrators, we bypass computationally intensive backpropagation through an ODE solver. We show that the method is robust to noise and provides a good approximation of the system Hamiltonian when the state variables are sampled from a noisy observation. In the numerical results, we show the performance of the method concerning Hamiltonian reconstruction and conservation, indicating its particular advantage for non-separable systems.

Safe Stabilizing Control for Polygonal Robots in Dynamic Elliptical Environments

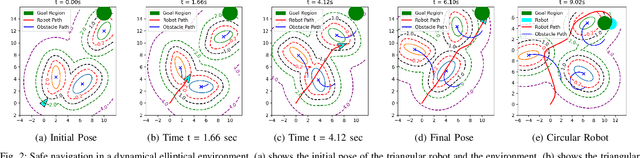
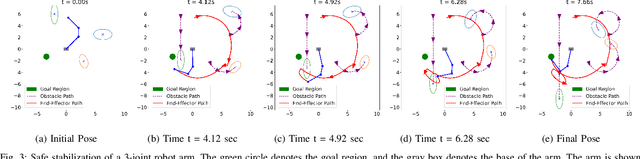
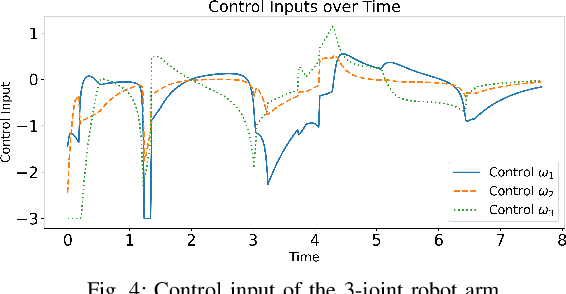
This paper addresses the challenge of safe navigation for rigid-body mobile robots in dynamic environments. We introduce an analytic approach to compute the distance between a polygon and an ellipse, and employ it to construct a control barrier function (CBF) for safe control synthesis. Existing CBF design methods for mobile robot obstacle avoidance usually assume point or circular robots, preventing their applicability to more realistic robot body geometries. Our work enables CBF designs that capture complex robot and obstacle shapes. We demonstrate the effectiveness of our approach in simulations highlighting real-time obstacle avoidance in constrained and dynamic environments for both mobile robots and multi-joint robot arms.

Simplifying Momentum-based Riemannian Submanifold Optimization

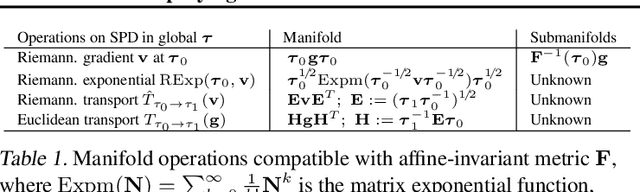
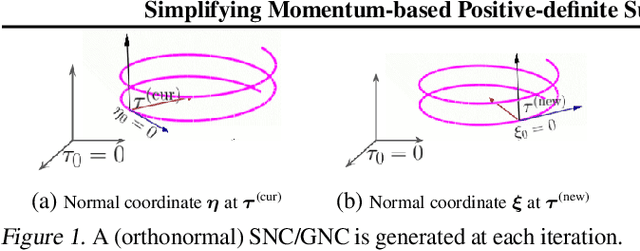
Riemannian submanifold optimization with momentum is computationally challenging because ensuring iterates remain on the submanifold often requires solving difficult differential equations. We simplify such optimization algorithms for the submanifold of symmetric positive-definite matrices with the affine invariant metric. We propose a generalized version of the Riemannian normal coordinates which dynamically trivializes the problem into a Euclidean unconstrained problem. We use our approach to explain and simplify existing approaches for structured covariances and develop efficient second-order optimizers for deep learning without explicit matrix inverses.

Lie Group Forced Variational Integrator Networks for Learning and Control of Robot Systems

Incorporating prior knowledge of physics laws and structural properties of dynamical systems into the design of deep learning architectures has proven to be a powerful technique for improving their computational efficiency and generalization capacity. Learning accurate models of robot dynamics is critical for safe and stable control. Autonomous mobile robots, including wheeled, aerial, and underwater vehicles, can be modeled as controlled Lagrangian or Hamiltonian rigid-body systems evolving on matrix Lie groups. In this paper, we introduce a new structure-preserving deep learning architecture, the Lie group Forced Variational Integrator Network (LieFVIN), capable of learning controlled Lagrangian or Hamiltonian dynamics on Lie groups, either from position-velocity or position-only data. By design, LieFVINs preserve both the Lie group structure on which the dynamics evolve and the symplectic structure underlying the Hamiltonian or Lagrangian systems of interest. The proposed architecture learns surrogate discrete-time flow maps allowing accurate and fast prediction without numerical-integrator, neural-ODE, or adjoint techniques, which are needed for vector fields. Furthermore, the learnt discrete-time dynamics can be utilized with computationally scalable discrete-time (optimal) control strategies.

Safe Control Synthesis with Uncertain Dynamics and Constraints

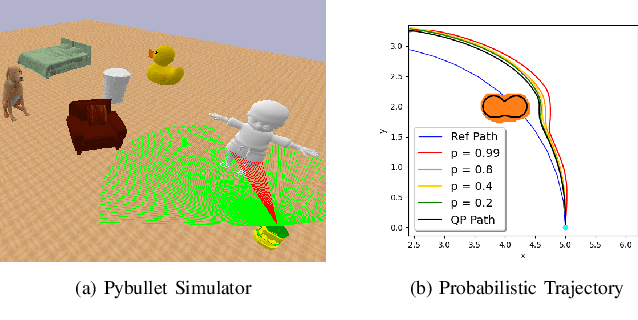
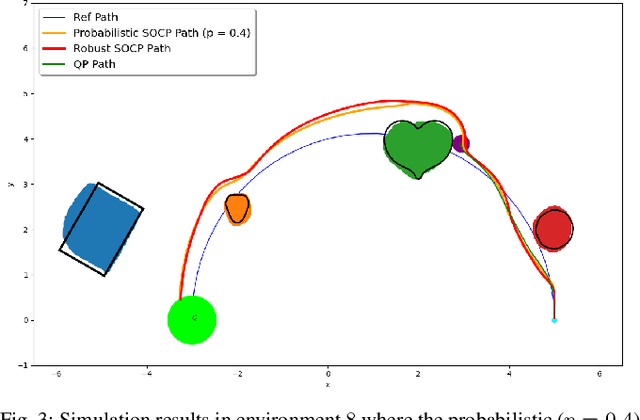
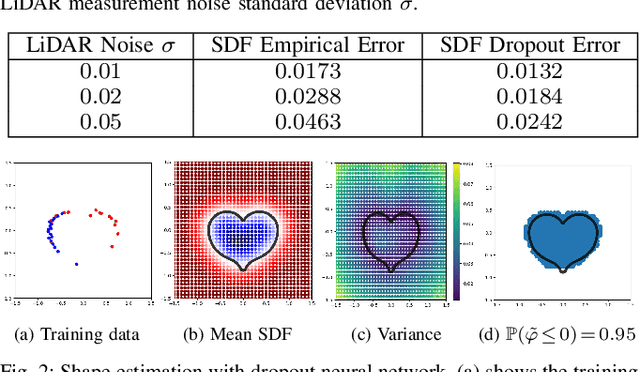
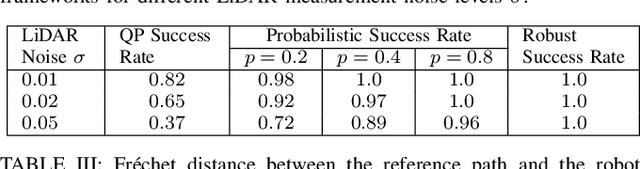
This paper considers safe control synthesis for dynamical systems in the presence of uncertainty in the dynamics model and the safety constraints that the system must satisfy. Our approach captures probabilistic and worst-case model errors and their effect on control Lyapunov function (CLF) and control barrier function (CBF) constraints in the control-synthesis optimization problem. We show that both the probabilistic and robust formulations lead to second-order cone programs (SOCPs), enabling safe and stable control synthesis that can be performed efficiently online. We evaluate our approach in PyBullet simulations of an autonomous robot navigating in unknown environments and compare the performance with a baseline CLF-CBF quadratic programming approach.