Understanding and Improving the Shampoo Optimizer via Kullback-Leibler Minimization

As an adaptive method, Shampoo employs a structured second-moment estimation, and its effectiveness has attracted growing attention. Prior work has primarily analyzed its estimation scheme through the Frobenius norm. Motivated by the natural connection between the second moment and a covariance matrix, we propose studying Shampoo's estimation as covariance estimation through the lens of Kullback-Leibler (KL) minimization. This alternative perspective reveals a previously hidden limitation, motivating improvements to Shampoo's design. Building on this insight, we develop a practical estimation scheme, termed KL-Shampoo, that eliminates Shampoo's reliance on Adam for stabilization, thereby removing the additional memory overhead introduced by Adam. Preliminary results show that KL-Shampoo improves Shampoo's performance, enabling it to stabilize without Adam and even outperform its Adam-stabilized variant, SOAP, in neural network pretraining.

Spectral-factorized Positive-definite Curvature Learning for NN Training

Many training methods, such as Adam(W) and Shampoo, learn a positive-definite curvature matrix and apply an inverse root before preconditioning. Recently, non-diagonal training methods, such as Shampoo, have gained significant attention; however, they remain computationally inefficient and are limited to specific types of curvature information due to the costly matrix root computation via matrix decomposition. To address this, we propose a Riemannian optimization approach that dynamically adapts spectral-factorized positive-definite curvature estimates, enabling the efficient application of arbitrary matrix roots and generic curvature learning. We demonstrate the efficacy and versatility of our approach in positive-definite matrix optimization and covariance adaptation for gradient-free optimization, as well as its efficiency in curvature learning for neural net training.

Training Data Attribution via Approximate Unrolled Differentiation

Many training data attribution (TDA) methods aim to estimate how a model's behavior would change if one or more data points were removed from the training set. Methods based on implicit differentiation, such as influence functions, can be made computationally efficient, but fail to account for underspecification, the implicit bias of the optimization algorithm, or multi-stage training pipelines. By contrast, methods based on unrolling address these issues but face scalability challenges. In this work, we connect the implicit-differentiation-based and unrolling-based approaches and combine their benefits by introducing Source, an approximate unrolling-based TDA method that is computed using an influence-function-like formula. While being computationally efficient compared to unrolling-based approaches, Source is suitable in cases where implicit-differentiation-based approaches struggle, such as in non-converged models and multi-stage training pipelines. Empirically, Source outperforms existing TDA techniques in counterfactual prediction, especially in settings where implicit-differentiation-based approaches fall short.

Can We Remove the Square-Root in Adaptive Gradient Methods? A Second-Order Perspective

Adaptive gradient optimizers like Adam(W) are the default training algorithms for many deep learning architectures, such as transformers. Their diagonal preconditioner is based on the gradient outer product which is incorporated into the parameter update via a square root. While these methods are often motivated as approximate second-order methods, the square root represents a fundamental difference. In this work, we investigate how the behavior of adaptive methods changes when we remove the root, i.e. strengthen their second-order motivation. Surprisingly, we find that such square-root-free adaptive methods close the generalization gap to SGD on convolutional architectures, while maintaining their root-based counterpart's performance on transformers. The second-order perspective also has practical benefits for the development of adaptive methods with non-diagonal preconditioner. In contrast to root-based counterparts like Shampoo, they do not require numerically unstable matrix square roots and therefore work well in low precision, which we demonstrate empirically. This raises important questions regarding the currently overlooked role of adaptivity for the success of adaptive methods since the success is often attributed to sign descent induced by the root.

Structured Inverse-Free Natural Gradient: Memory-Efficient & Numerically-Stable KFAC for Large Neural Nets

Second-order methods for deep learning -- such as KFAC -- can be useful for neural net training. However, they are often memory-inefficient and numerically unstable for low-precision training since their preconditioning Kronecker factors are dense, and require high-precision matrix inversion or decomposition. Consequently, such methods are not widely used for training large neural networks such as transformer-based models. We address these two issues by (i) formulating an inverse-free update of KFAC and (ii) imposing structures in each of the Kronecker factors, resulting in a method we term structured inverse-free natural gradient descent (SINGD). On large modern neural networks, we show that, in contrast to KFAC, SINGD is memory efficient and numerically robust, and often outperforms AdamW even in half precision. Hence, our work closes a gap between first-order and second-order methods in modern low precision training for large neural nets.

Simplifying Momentum-based Riemannian Submanifold Optimization

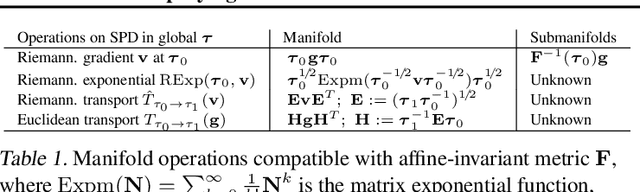
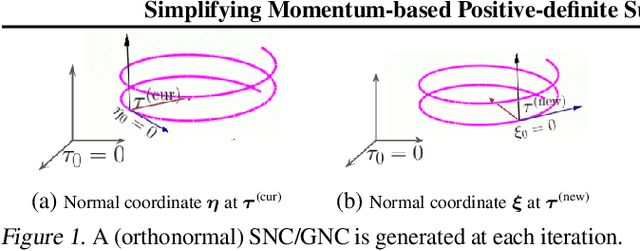
Riemannian submanifold optimization with momentum is computationally challenging because ensuring iterates remain on the submanifold often requires solving difficult differential equations. We simplify such optimization algorithms for the submanifold of symmetric positive-definite matrices with the affine invariant metric. We propose a generalized version of the Riemannian normal coordinates which dynamically trivializes the problem into a Euclidean unconstrained problem. We use our approach to explain and simplify existing approaches for structured covariances and develop efficient second-order optimizers for deep learning without explicit matrix inverses.

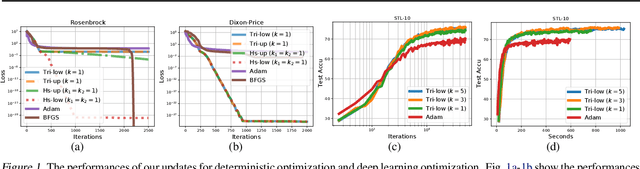
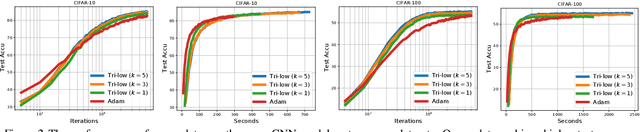
Structured second-order methods via natural gradient descent

In this paper, we propose new structured second-order methods and structured adaptive-gradient methods obtained by performing natural-gradient descent on structured parameter spaces. Natural-gradient descent is an attractive approach to design new algorithms in many settings such as gradient-free, adaptive-gradient, and second-order methods. Our structured methods not only enjoy a structural invariance but also admit a simple expression. Finally, we test the efficiency of our proposed methods on both deterministic non-convex problems and deep learning problems.

Tractable structured natural gradient descent using local parameterizations

Natural-gradient descent on structured parameter spaces (e.g., low-rank covariances) is computationally challenging due to complicated inverse Fisher-matrix computations. We address this issue for optimization, inference, and search problems by using \emph{local-parameter coordinates}. Our method generalizes an existing evolutionary-strategy method, recovers Newton and Riemannian-gradient methods as special cases, and also yields new tractable natural-gradient algorithms for learning flexible covariance structures of Gaussian and Wishart-based distributions via \emph{matrix groups}. We show results on a range of applications on deep learning, variational inference, and evolution strategies. Our work opens a new direction for scalable structured geometric methods via local parameterizations.

Handling the Positive-Definite Constraint in the Bayesian Learning Rule

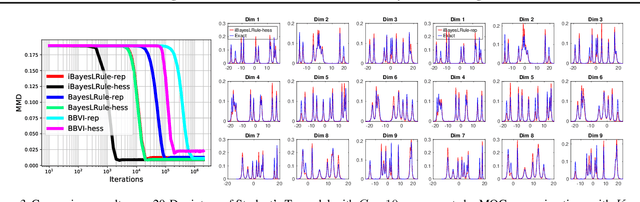
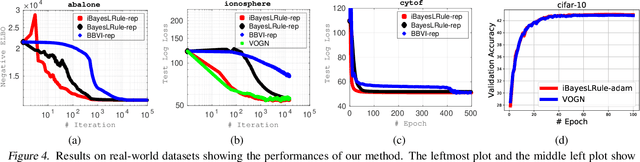
The Bayesian learning rule is a recently proposed variational inference method, which not only contains many existing learning algorithms as special cases but also enables the design of new algorithms. Unfortunately, when posterior parameters lie in an open constraint set, the rule may not satisfy the constraints and requires line-searches which could slow down the algorithm. In this paper, we fix this issue for the positive-definite constraint by proposing an improved rule that naturally handles the constraint. Our modification is obtained using Riemannian gradient methods, and is valid when the approximation attains a \emph{block-coordinate natural parameterization} (e.g., Gaussian distributions and their mixtures). Our method outperforms existing methods without any significant increase in computation. Our work makes it easier to apply the learning rule in the presence of positive-definite constraints in parameter spaces.

Stein's Lemma for the Reparameterization Trick with Exponential Family Mixtures

Stein's method (Stein, 1973; 1981) is a powerful tool for statistical applications, and has had a significant impact in machine learning. Stein's lemma plays an essential role in Stein's method. Previous applications of Stein's lemma either required strong technical assumptions or were limited to Gaussian distributions with restricted covariance structures. In this work, we extend Stein's lemma to exponential-family mixture distributions including Gaussian distributions with full covariance structures. Our generalization enables us to establish a connection between Stein's lemma and the reparamterization trick to derive gradients of expectations of a large class of functions under weak assumptions. Using this connection, we can derive many new reparameterizable gradient-identities that goes beyond the reach of existing works. For example, we give gradient identities when expectation is taken with respect to Student's t-distribution, skew Gaussian, exponentially modified Gaussian, and normal inverse Gaussian.