Tractable structured natural gradient descent using local parameterizations
Paper and Code
Mar 04, 2021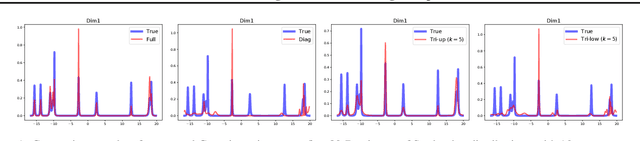
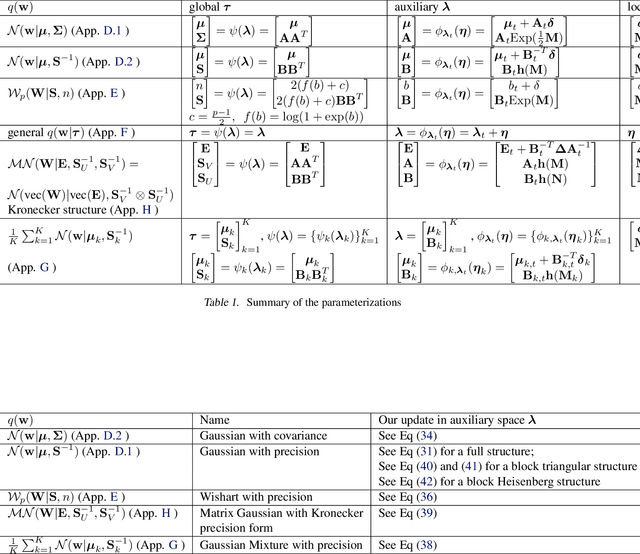
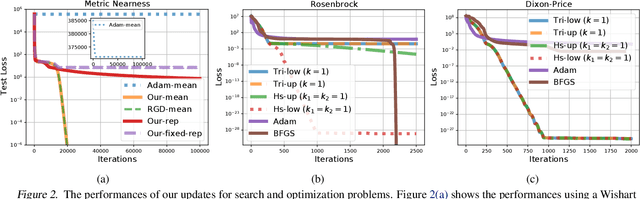

Natural-gradient descent on structured parameter spaces (e.g., low-rank covariances) is computationally challenging due to complicated inverse Fisher-matrix computations. We address this issue for optimization, inference, and search problems by using \emph{local-parameter coordinates}. Our method generalizes an existing evolutionary-strategy method, recovers Newton and Riemannian-gradient methods as special cases, and also yields new tractable natural-gradient algorithms for learning flexible covariance structures of Gaussian and Wishart-based distributions via \emph{matrix groups}. We show results on a range of applications on deep learning, variational inference, and evolution strategies. Our work opens a new direction for scalable structured geometric methods via local parameterizations.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge