Mohammad Emtiyaz Khan
RIKEN Center for AI Project, Tokyo, Japan
Compact Memory for Continual Logistic Regression
Nov 12, 2025Abstract:Despite recent progress, continual learning still does not match the performance of batch training. To avoid catastrophic forgetting, we need to build compact memory of essential past knowledge, but no clear solution has yet emerged, even for shallow neural networks with just one or two layers. In this paper, we present a new method to build compact memory for logistic regression. Our method is based on a result by Khan and Swaroop [2021] who show the existence of optimal memory for such models. We formulate the search for the optimal memory as Hessian-matching and propose a probabilistic PCA method to estimate them. Our approach can drastically improve accuracy compared to Experience Replay. For instance, on Split-ImageNet, we get 60% accuracy compared to 30% obtained by replay with memory-size equivalent to 0.3% of the data size. Increasing the memory size to 2% further boosts the accuracy to 74%, closing the gap to the batch accuracy of 77.6% on this task. Our work opens a new direction for building compact memory that can also be useful in the future for continual deep learning.
Information Geometry of Variational Bayes
Sep 19, 2025
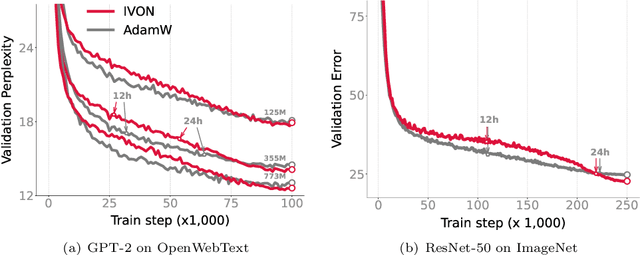
Abstract:We highlight a fundamental connection between information geometry and variational Bayes (VB) and discuss its consequences for machine learning. Under certain conditions, a VB solution always requires estimation or computation of natural gradients. We show several consequences of this fact by using the natural-gradient descent algorithm of Khan and Rue (2023) called the Bayesian Learning Rule (BLR). These include (i) a simplification of Bayes' rule as addition of natural gradients, (ii) a generalization of quadratic surrogates used in gradient-based methods, and (iii) a large-scale implementation of VB algorithms for large language models. Neither the connection nor its consequences are new but we further emphasize the common origins of the two fields of information geometry and Bayes with a hope to facilitate more work at the intersection of the two fields.
Optimization Guarantees for Square-Root Natural-Gradient Variational Inference
Jul 10, 2025Abstract:Variational inference with natural-gradient descent often shows fast convergence in practice, but its theoretical convergence guarantees have been challenging to establish. This is true even for the simplest cases that involve concave log-likelihoods and use a Gaussian approximation. We show that the challenge can be circumvented for such cases using a square-root parameterization for the Gaussian covariance. This approach establishes novel convergence guarantees for natural-gradient variational-Gaussian inference and its continuous-time gradient flow. Our experiments demonstrate the effectiveness of natural gradient methods and highlight their advantages over algorithms that use Euclidean or Wasserstein geometries.
Knowledge Adaptation as Posterior Correction
Jun 17, 2025Abstract:Adaptation is the holy grail of intelligence, but even the best AI models (like GPT) lack the adaptivity of toddlers. So the question remains: how can machines adapt quickly? Despite a lot of progress on model adaptation to facilitate continual and federated learning, as well as model merging, editing, unlearning, etc., little is known about the mechanisms by which machines can naturally learn to adapt in a similar way as humans and animals. Here, we show that all such adaptation methods can be seen as different ways of `correcting' the approximate posteriors. More accurate posteriors lead to smaller corrections, which in turn imply quicker adaptation. The result is obtained by using a dual-perspective of the Bayesian Learning Rule of Khan and Rue (2023) where interference created during adaptation is characterized by the natural-gradient mismatch over the past data. We present many examples to demonstrate the use of posterior-correction as a natural mechanism for the machines to learn to adapt quickly.
Improving LoRA with Variational Learning
Jun 17, 2025Abstract:Bayesian methods have recently been used to improve LoRA finetuning and, although they improve calibration, their effect on other metrics (such as accuracy) is marginal and can sometimes even be detrimental. Moreover, Bayesian methods also increase computational overheads and require additional tricks for them to work well. Here, we fix these issues by using a recently proposed variational algorithm called IVON. We show that IVON is easy to implement and has similar costs to AdamW, and yet it can also drastically improve many metrics by using a simple posterior pruning technique. We present extensive results on billion-scale LLMs (Llama and Qwen series) going way beyond the scale of existing applications of IVON. For example, we finetune a Llama-3.2-3B model on a set of commonsense reasoning tasks and improve accuracy over AdamW by 1.3% and reduce ECE by 5.4%, outperforming AdamW and other recent Bayesian methods like Laplace-LoRA and BLoB. Overall, our results show that variational learning with IVON can effectively improve LoRA finetuning.
Federated ADMM from Bayesian Duality
Jun 16, 2025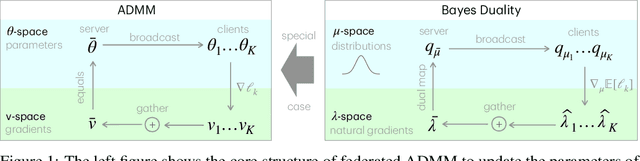
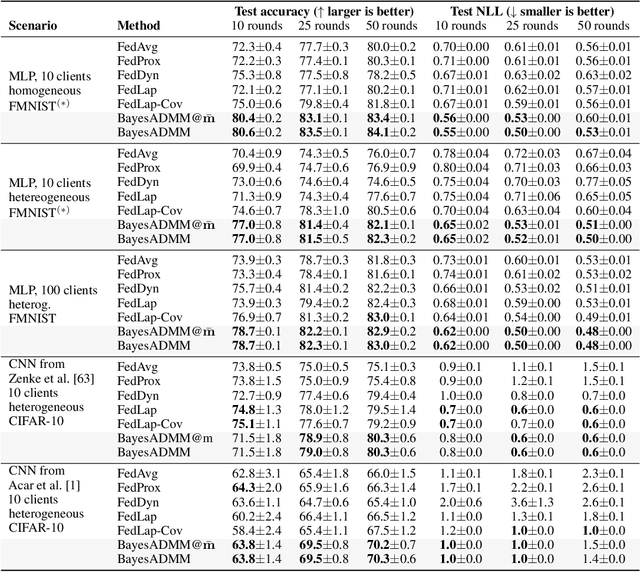

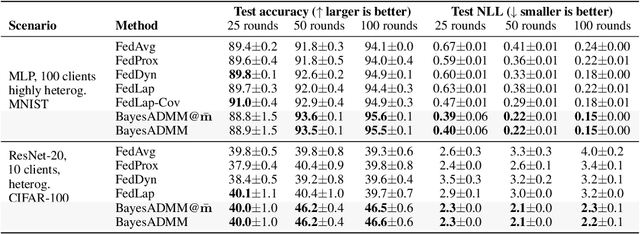
Abstract:ADMM is a popular method for federated deep learning which originated in the 1970s and, even though many new variants of it have been proposed since then, its core algorithmic structure has remained unchanged. Here, we take a major departure from the old structure and present a fundamentally new way to derive and extend federated ADMM. We propose to use a structure called Bayesian Duality which exploits a duality of the posterior distributions obtained by solving a variational-Bayesian reformulation of the original problem. We show that this naturally recovers the original ADMM when isotropic Gaussian posteriors are used, and yields non-trivial extensions for other posterior forms. For instance, full-covariance Gaussians lead to Newton-like variants of ADMM, while diagonal covariances result in a cheap Adam-like variant. This is especially useful to handle heterogeneity in federated deep learning, giving up to 7% accuracy improvements over recent baselines. Our work opens a new Bayesian path to improve primal-dual methods.
Variational Learning Finds Flatter Solutions at the Edge of Stability
Jun 15, 2025Abstract:Variational Learning (VL) has recently gained popularity for training deep neural networks and is competitive to standard learning methods. Part of its empirical success can be explained by theories such as PAC-Bayes bounds, minimum description length and marginal likelihood, but there are few tools to unravel the implicit regularization in play. Here, we analyze the implicit regularization of VL through the Edge of Stability (EoS) framework. EoS has previously been used to show that gradient descent can find flat solutions and we extend this result to VL to show that it can find even flatter solutions. This is obtained by controlling the posterior covariance and the number of Monte Carlo samples from the posterior. These results are derived in a similar fashion as the standard EoS literature for deep learning, by first deriving a result for a quadratic problem and then extending it to deep neural networks. We empirically validate these findings on a wide variety of large networks, such as ResNet and ViT, to find that the theoretical results closely match the empirical ones. Ours is the first work to analyze the EoS dynamics in VL.
Variational Visual Question Answering
May 14, 2025Abstract:Despite remarkable progress in multimodal models for Visual Question Answering (VQA), there remain major reliability concerns because the models can often be overconfident and miscalibrated, especially in out-of-distribution (OOD) settings. Plenty has been done to address such issues for unimodal models, but little work exists for multimodal cases. Here, we address unreliability in multimodal models by proposing a Variational VQA approach. Specifically, instead of fine-tuning vision-language models by using AdamW, we employ a recently proposed variational algorithm called IVON, which yields a posterior distribution over model parameters. Through extensive experiments, we show that our approach improves calibration and abstentions without sacrificing the accuracy of AdamW. For instance, compared to AdamW fine-tuning, we reduce Expected Calibration Error by more than 50% compared to the AdamW baseline and raise Coverage by 4% vs. SOTA (for a fixed risk of 1%). In the presence of distribution shifts, the performance gain is even higher, achieving 8% Coverage (@ 1% risk) improvement vs. SOTA when 50% of test cases are OOD. Overall, we present variational learning as a viable option to enhance the reliability of multimodal models.
Variational Learning Induces Adaptive Label Smoothing
Feb 11, 2025Abstract:We show that variational learning naturally induces an adaptive label smoothing where label noise is specialized for each example. Such label-smoothing is useful to handle examples with labeling errors and distribution shifts, but designing a good adaptivity strategy is not always easy. We propose to skip this step and simply use the natural adaptivity induced during the optimization of a variational objective. We show empirical results where a variational algorithm called IVON outperforms traditional label smoothing and yields adaptivity strategies similar to those of an existing approach. By connecting Bayesian methods to label smoothing, our work provides a new way to handle overconfident predictions.
Connecting Federated ADMM to Bayes
Jan 28, 2025Abstract:We provide new connections between two distinct federated learning approaches based on (i) ADMM and (ii) Variational Bayes (VB), and propose new variants by combining their complementary strengths. Specifically, we show that the dual variables in ADMM naturally emerge through the 'site' parameters used in VB with isotropic Gaussian covariances. Using this, we derive two versions of ADMM from VB that use flexible covariances and functional regularisation, respectively. Through numerical experiments, we validate the improvements obtained in performance. The work shows connection between two fields that are believed to be fundamentally different and combines them to improve federated learning.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge