Variational Learning Finds Flatter Solutions at the Edge of Stability

Variational Learning (VL) has recently gained popularity for training deep neural networks and is competitive to standard learning methods. Part of its empirical success can be explained by theories such as PAC-Bayes bounds, minimum description length and marginal likelihood, but there are few tools to unravel the implicit regularization in play. Here, we analyze the implicit regularization of VL through the Edge of Stability (EoS) framework. EoS has previously been used to show that gradient descent can find flat solutions and we extend this result to VL to show that it can find even flatter solutions. This is obtained by controlling the posterior covariance and the number of Monte Carlo samples from the posterior. These results are derived in a similar fashion as the standard EoS literature for deep learning, by first deriving a result for a quadratic problem and then extending it to deep neural networks. We empirically validate these findings on a wide variety of large networks, such as ResNet and ViT, to find that the theoretical results closely match the empirical ones. Ours is the first work to analyze the EoS dynamics in VL.

A Dataless Reinforcement Learning Approach to Rounding Hyperplane Optimization for Max-Cut

The Maximum Cut (MaxCut) problem is NP-Complete, and obtaining its optimal solution is NP-hard in the worst case. As a result, heuristic-based algorithms are commonly used, though their design often requires significant domain expertise. More recently, learning-based methods trained on large (un)labeled datasets have been proposed; however, these approaches often struggle with generalizability and scalability. A well-known approximation algorithm for MaxCut is the Goemans-Williamson (GW) algorithm, which relaxes the Quadratic Unconstrained Binary Optimization (QUBO) formulation into a semidefinite program (SDP). The GW algorithm then applies hyperplane rounding by uniformly sampling a random hyperplane to convert the SDP solution into binary node assignments. In this paper, we propose a training-data-free approach based on a non-episodic reinforcement learning formulation, in which an agent learns to select improved rounding hyperplanes that yield better cuts than those produced by the GW algorithm. By optimizing over a Markov Decision Process (MDP), our method consistently achieves better cuts across large-scale graphs with varying densities and degree distributions.

UGoDIT: Unsupervised Group Deep Image Prior Via Transferable Weights

Recent advances in data-centric deep generative models have led to significant progress in solving inverse imaging problems. However, these models (e.g., diffusion models (DMs)) typically require large amounts of fully sampled (clean) training data, which is often impractical in medical and scientific settings such as dynamic imaging. On the other hand, training-data-free approaches like the Deep Image Prior (DIP) do not require clean ground-truth images but suffer from noise overfitting and can be computationally expensive as the network parameters need to be optimized for each measurement set independently. Moreover, DIP-based methods often overlook the potential of learning a prior using a small number of sub-sampled measurements (or degraded images) available during training. In this paper, we propose UGoDIT, an Unsupervised Group DIP via Transferable weights, designed for the low-data regime where only a very small number, M, of sub-sampled measurement vectors are available during training. Our method learns a set of transferable weights by optimizing a shared encoder and M disentangled decoders. At test time, we reconstruct the unseen degraded image using a DIP network, where part of the parameters are fixed to the learned weights, while the remaining are optimized to enforce measurement consistency. We evaluate UGoDIT on both medical (multi-coil MRI) and natural (super resolution and non-linear deblurring) image recovery tasks under various settings. Compared to recent standalone DIP methods, UGoDIT provides accelerated convergence and notable improvement in reconstruction quality. Furthermore, our method achieves performance competitive with SOTA DM-based and supervised approaches, despite not requiring large amounts of clean training data.

Learning Dynamics of Deep Linear Networks Beyond the Edge of Stability

Deep neural networks trained using gradient descent with a fixed learning rate $\eta$ often operate in the regime of "edge of stability" (EOS), where the largest eigenvalue of the Hessian equilibrates about the stability threshold $2/\eta$. In this work, we present a fine-grained analysis of the learning dynamics of (deep) linear networks (DLNs) within the deep matrix factorization loss beyond EOS. For DLNs, loss oscillations beyond EOS follow a period-doubling route to chaos. We theoretically analyze the regime of the 2-period orbit and show that the loss oscillations occur within a small subspace, with the dimension of the subspace precisely characterized by the learning rate. The crux of our analysis lies in showing that the symmetry-induced conservation law for gradient flow, defined as the balancing gap among the singular values across layers, breaks at EOS and decays monotonically to zero. Overall, our results contribute to explaining two key phenomena in deep networks: (i) shallow models and simple tasks do not always exhibit EOS; and (ii) oscillations occur within top features. We present experiments to support our theory, along with examples demonstrating how these phenomena occur in nonlinear networks and how they differ from those which have benign landscape such as in DLNs.

Understanding Untrained Deep Models for Inverse Problems: Algorithms and Theory

In recent years, deep learning methods have been extensively developed for inverse imaging problems (IIPs), encompassing supervised, self-supervised, and generative approaches. Most of these methods require large amounts of labeled or unlabeled training data to learn effective models. However, in many practical applications, such as medical image reconstruction, extensive training datasets are often unavailable or limited. A significant milestone in addressing this challenge came in 2018 with the work of Ulyanov et al., which introduced the Deep Image Prior (DIP)--the first training-data-free neural network method for IIPs. Unlike conventional deep learning approaches, DIP requires only a convolutional neural network, the noisy measurements, and a forward operator. By leveraging the implicit regularization of deep networks initialized with random noise, DIP can learn and restore image structures without relying on external datasets. However, a well-known limitation of DIP is its susceptibility to overfitting, primarily due to the over-parameterization of the network. In this tutorial paper, we provide a comprehensive review of DIP, including a theoretical analysis of its training dynamics. We also categorize and discuss recent advancements in DIP-based methods aimed at mitigating overfitting, including techniques such as regularization, network re-parameterization, and early stopping. Furthermore, we discuss approaches that combine DIP with pre-trained neural networks, present empirical comparison results against data-centric methods, and highlight open research questions and future directions.

Learnable Scaled Gradient Descent for Guaranteed Robust Tensor PCA

Robust tensor principal component analysis (RTPCA) aims to separate the low-rank and sparse components from multi-dimensional data, making it an essential technique in the signal processing and computer vision fields. Recently emerging tensor singular value decomposition (t-SVD) has gained considerable attention for its ability to better capture the low-rank structure of tensors compared to traditional matrix SVD. However, existing methods often rely on the computationally expensive tensor nuclear norm (TNN), which limits their scalability for real-world tensors. To address this issue, we explore an efficient scaled gradient descent (SGD) approach within the t-SVD framework for the first time, and propose the RTPCA-SGD method. Theoretically, we rigorously establish the recovery guarantees of RTPCA-SGD under mild assumptions, demonstrating that with appropriate parameter selection, it achieves linear convergence to the true low-rank tensor at a constant rate, independent of the condition number. To enhance its practical applicability, we further propose a learnable self-supervised deep unfolding model, which enables effective parameter learning. Numerical experiments on both synthetic and real-world datasets demonstrate the superior performance of the proposed methods while maintaining competitive computational efficiency, especially consuming less time than RTPCA-TNN.

Pruning Unrolled Networks (PUN) at Initialization for MRI Reconstruction Improves Generalization

Deep learning methods are highly effective for many image reconstruction tasks. However, the performance of supervised learned models can degrade when applied to distinct experimental settings at test time or in the presence of distribution shifts. In this study, we demonstrate that pruning deep image reconstruction networks at training time can improve their robustness to distribution shifts. In particular, we consider unrolled reconstruction architectures for accelerated magnetic resonance imaging and introduce a method for pruning unrolled networks (PUN) at initialization. Our experiments demonstrate that when compared to traditional dense networks, PUN offers improved generalization across a variety of experimental settings and even slight performance gains on in-distribution data.

SITCOM: Step-wise Triple-Consistent Diffusion Sampling for Inverse Problems

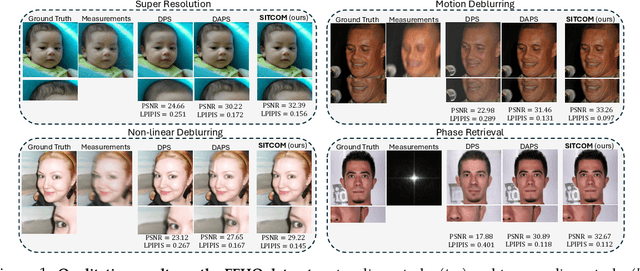
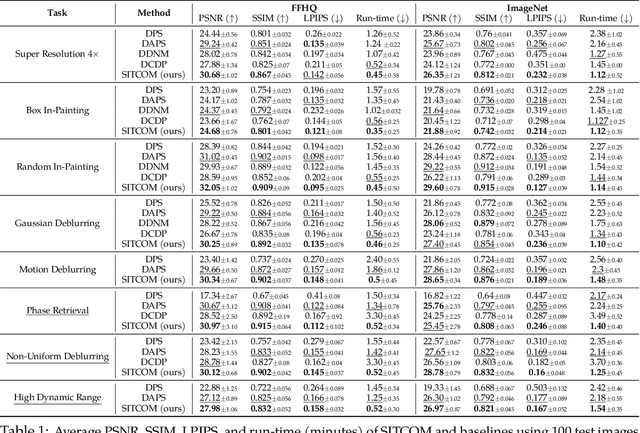
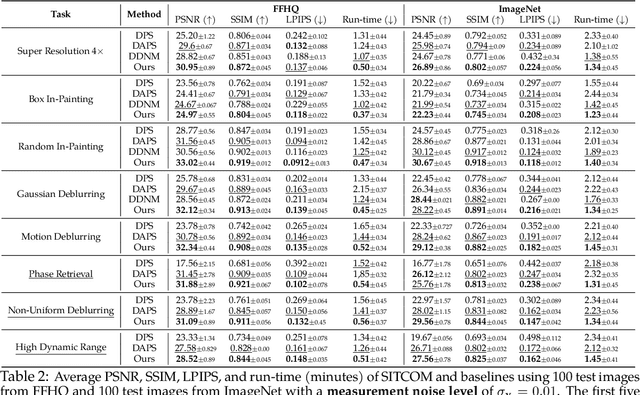
Diffusion models (DMs) are a class of generative models that allow sampling from a distribution learned over a training set. When applied to solving inverse imaging problems (IPs), the reverse sampling steps of DMs are typically modified to approximately sample from a measurement-conditioned distribution in the image space. However, these modifications may be unsuitable for certain settings (such as in the presence of measurement noise) and non-linear tasks, as they often struggle to correct errors from earlier sampling steps and generally require a large number of optimization and/or sampling steps. To address these challenges, we state three conditions for achieving measurement-consistent diffusion trajectories. Building on these conditions, we propose a new optimization-based sampling method that not only enforces the standard data manifold measurement consistency and forward diffusion consistency, as seen in previous studies, but also incorporates backward diffusion consistency that maintains a diffusion trajectory by optimizing over the input of the pre-trained model at every sampling step. By enforcing these conditions, either implicitly or explicitly, our sampler requires significantly fewer reverse steps. Therefore, we refer to our accelerated method as Step-wise Triple-Consistent Sampling (SITCOM). Compared to existing state-of-the-art baseline methods, under different levels of measurement noise, our extensive experiments across five linear and three non-linear image restoration tasks demonstrate that SITCOM achieves competitive or superior results in terms of standard image similarity metrics while requiring a significantly reduced run-time across all considered tasks.

uDiG-DIP: Unrolled Diffusion-Guided Deep Image Prior For Medical Image Reconstruction

Deep learning (DL) methods have been extensively applied to various image recovery problems, including magnetic resonance imaging (MRI) and computed tomography (CT) reconstruction. Beyond supervised models, other approaches have been recently explored including two key recent schemes: Deep Image Prior (DIP) that is an unsupervised scan-adaptive method that leverages the network architecture as implicit regularization but can suffer from noise overfitting, and diffusion models (DMs), where the sampling procedure of a pre-trained generative model is modified to allow sampling from the measurement-conditioned distribution through approximations. In this paper, we propose combining DIP and DMs for MRI and CT reconstruction, motivated by (i) the impact of the DIP network input and (ii) the use of DMs as diffusion purifiers (DPs). Specifically, we propose an unrolled procedure that iteratively optimizes the DIP network with a DM-refined adaptive input using a loss with data consistency and autoencoding terms. We term the approach unrolled Diffusion-Guided DIP (uDiG-DIP). Our experimental results demonstrate that uDiG-DIP achieves superior reconstruction results compared to leading DM-based baselines and the original DIP for MRI and CT tasks.

Learning Robust Features for Scatter Removal and Reconstruction in Dynamic ICF X-Ray Tomography

Density reconstruction from X-ray projections is an important problem in radiography with key applications in scientific and industrial X-ray computed tomography (CT). Often, such projections are corrupted by unknown sources of noise and scatter, which when not properly accounted for, can lead to significant errors in density reconstruction. In the setting of this problem, recent deep learning-based methods have shown promise in improving the accuracy of density reconstruction. In this article, we propose a deep learning-based encoder-decoder framework wherein the encoder extracts robust features from noisy/corrupted X-ray projections and the decoder reconstructs the density field from the features extracted by the encoder. We explore three options for the latent-space representation of features: physics-inspired supervision, self-supervision, and no supervision. We find that variants based on self-supervised and physicsinspired supervised features perform better over a range of unknown scatter and noise. In extreme noise settings, the variant with self-supervised features performs best. After investigating further details of the proposed deep-learning methods, we conclude by demonstrating that the newly proposed methods are able to achieve higher accuracy in density reconstruction when compared to a traditional iterative technique.